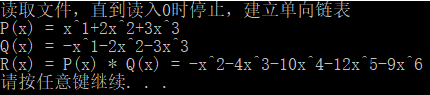题目要求
从字符文件输入两个多项式的非零系数及对应的指数,建立多项式的链式存储结构,计算这两个多项式的乘积,输出乘积多项式的全部非零系数及对应的指数到另一字符文件中。
算法原理
两个多项式的乘法,可以借助两个多项式的加法的算法来实现。
设:
则:
例如: ,
,
则:
数据结构设计
采用带附加头结点单向链表;每个结点包括双精度类型的系数域、整型类型的指数域和一个指针域。
typedef struct polynode
{double c; //系数int e; //指数struct polynode *next; //指针域,要求结点按指数e升序连接
}PNode,*Polyn; //PNode为结点类型,Polyn为结点指针类型程序代码
#include <iostream>
#include <fstream>
#include <string.h>
using namespace std;
//定义结点及结点指针数据类型
typedef struct polynode
{double c; //系数int e; //指数struct polynode *next; //要求结点按指数e升序连接
}PNode,*Polyn; //PNode为结点类型,Polyn为结点指针类型
Polyn h1, h2; //两个多项式P(x),Q(x)的头结点
double a[20]; //数组a保存系数
int b[20]; //数组b保存指数
void Read(char *s) //读取数据,s代入不同的文件名
{double c;int i = 0, e;ifstream infile(s);if (!infile) //打开文件失败输出提示信息{cout << "file open error!" << endl;exit(0);}while (1) //打开成功,将系数和指数保存在两个数组中{infile >> c >> e;if (infile.eof())break;a[i] = c;b[i] = e;i++;}infile.close();
}
void Write(Polyn h) //输出函数,将结果输出到文件中,h为链表头结点
{ofstream outfile("multiply.txt"); //输出文件名为multiply.txtPolyn p = h->next; //去掉附加头结点if (!outfile) //打开文件失败输出提示信息{cout << "file open error!" << endl;exit(0);}if (!p) //第一个结点为空,表示运算结果为0outfile << "0" << endl;while (p) //p不为空,依次输出系数和指数{outfile << p->c << " " << p->e << endl;p = p->next;}outfile.close();
}void clearArray() { //清空数组memset(a, 0, sizeof(a));memset(b, 0, sizeof(b));
}Polyn Create(char *s) //先入先出建立链表,s代入不同的文件名
{int i = 0; //i用于记录数组下标Polyn h, last, p;h = new PNode;h->next = NULL; //h为附加头结点last = h;clearArray();Read(s); //从文件中读取系数和指数while (a[i]!=0){p = new PNode;p->c = a[i];p->e = b[i];p->next = NULL; //建新结点last->next = p;last = p; //新结点插入到链表尾i++;}return h;
}void PrintPoly(Polyn h) //按多项式的形式将结果打印到控制台界面中
{Polyn p = h->next;if (!p) //所得结果为空,则输出0cout << "0" << endl;while (p){if (p->next) //p不是尾结点{if (p->next->c < 0) //p的后继结点的系数小于0,不输出符号 + {if (p->c == -1) //p的后继结点的系数等于-1{cout << "-x^" << p->e;p = p->next;}else if (p->c == 1) //p的后继结点的系数等于1{cout << "x^" << p->e;p = p->next;}else{cout << p->c << "x^" << p->e;p = p->next;}}else if (p->next->c > 0) //p的后继结点的系数大于0,需输出符号+{if (p->c == 1) //p的后继结点的系数等于1{cout << "x^" << p->e << "+";p = p->next;}else if (p->c == -1) //p的后继结点的系数等于-1{cout << "-x^" << p->e << "+";p = p->next;}else{cout << p->c << "x^" << p->e << "+";p = p->next;}}}else //p是尾结点,需在结尾输出换行{if (p->c < 0) //p的指数小于0{if (p->c == -1){cout << "-x^" << p->e << endl;p = p->next;}else{cout << p->c << "x^" << p->e << endl;p = p->next;}}else if (p->c > 0) //p的指数大于0{if (p->c == 1){cout << "x^" << p->e << endl;p = p->next;}else{cout << p->c << "x^" << p->e << endl;p = p->next;} } }}
}
void CreateNode(Polyn &p) //创建新结点
{p = new PNode;
}
void DeleteNode(Polyn &p) //删除结点
{delete p;
}
Polyn add(Polyn h1, Polyn h2) //实现两个多项式的相加,返回和式头指针
{Polyn p1, p2, p3, h, p; //h为和式R(x)的附加头结点指针p1 = h1->next;p2 = h2->next;CreateNode(h);p3 = h;while (p1&&p2){if (p1->e < p2->e) //p1的指数大于p2,先保存p1结点{p = p1;p1 = p1->next;}else if (p2->e < p1->e) //p2的指数大于p1,先保存p2结点{p = p2;p2 = p2->next;}else //p1与p2指数相等时{p1->c += p2->c; //系数相加,结果保存在p1中if (p1->c == 0) //系数之和为0,则删除该结点{p = p1;p1 = p1->next;DeleteNode(p); //删除结点p = p2;p2 = p2->next;DeleteNode(p);continue;}p = p2; //系数之和不为0时,先删除p2结点p2 = p2->next;DeleteNode(p);p = p1; //将p1连接到p中p1 = p1->next;}p3->next = p; //插入p结点至和式末尾p3 = p;}if (p1) //p1没有结束,将p1后面所有的结点连接到和式p3->next = p1;else if (p2) //p2没有结束,将p2后面所有的结点连接到和式p3->next = p2;elsep3->next = NULL;h1->next = h2->next = NULL; //清空h1和h2链表return h;
}
Polyn mul(Polyn hp, Polyn hq) //实现两个多项式的相乘
{Polyn hr, ht, q, p, pt;CreateNode(hr);hr->next = NULL; //R(x) = 0CreateNode(ht);ht->next = NULL; //T(x) = 0q = hq->next;while (q){pt = ht;p = hp->next;while (p){CreateNode(pt->next); //创建新的尾结点pt = pt->next;pt->c = p->c*q->c; //系数相乘pt->e = p->e + q->e; //指数相加p = p->next;}pt->next = NULL;q = q->next;p = add(hr, ht); //实现R(x) = R(x) + T(x)DeleteNode(hr);hr = p;}DeleteNode(ht);return hr;
}
int main()
{Polyn h1, h2, h3; //定义单向链表附加头结点指针cout << "读取文件,直到读入0时停止,建立单向链表" << endl;h1 = Create("polynode1.txt");h2 = Create("polynode2.txt");cout << "P(x) = ";PrintPoly(h1);cout << "Q(x) = ";PrintPoly(h2);h3 = mul(h1, h2);cout << "R(x) = P(x) * Q(x) = ";PrintPoly(h3);Write(h3); //写入文件return 0;
}示例
(1) P(x) 1 2 2 3 0
Q(x) 1 -2 2 -3 0
输出结果为:
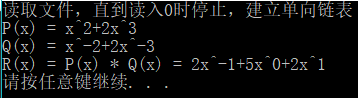
(2)P(x) 1 1 2 2 3 3 0
Q(x) -1 1 -2 2 -3 3 0
输出结果为: