软件定义存储源于VMware公司于2012年提出的软件定义的数据中心(SDDC)。存储作为软件定义的数据中心不可或缺的一部分,其以虚拟化为基础,但又不仅限于虚拟化。存储虚拟化一般只能在专门的硬件设备上应用,很多设备都是经过专门的定做才能够进行存储虚拟化。而软件定义存储则没有设备限制,可以简单地理解为存储的管理程序(类似于软件定义计算中虚拟机管理程序VMM)。
软件定义存储是对现有操作系统和管理软件的一个结合,能够完整实现我们对存储系统的部署、管理、监控、调整等多种要求,可以给我们的存储系统带来敏捷、高可用、跨数据中心支持等特点。
软件定义存储通常具有如下几大特性:
·开放性(Open)
· 简单化(Simplified)
· 可扩展性(Scalable)
开放的软件定义存储主要指两个维度:API的标准化与可编程平台的支持。使用标准的开放的API,任何人都可以基于此而构建数据服务。这一点不仅有利于大的企业,对于创业公司更加方便,因为它为客户提供一个开放式底层的存储平台可以利用。开放的API必然是用来支撑一套可编程架构,可以实现一次编程、多次运行、无处不在的数据服务。此二者结合起来促进开放式开发社区的全局数据和自动化服务的交付。
简单化是所有存储应用与用户追求的目标,包括统一的管理接口与界面、自动化的存储配置与部署,便捷的存储扩展、升级及优化。现代存储系统自20世纪中叶诞生以来一直是一个非常专业化的领域,它的复杂性与挑战性令另很多人望而止步,但是软件定义存储的出现在逐渐颠覆这一现象,存储变得更容易被管理,更容易满足客户与应用的需求。
可扩展性指的是存储系统中对同构或异构存储解决方案、服务的可接入性,它在一定程度上与系统的开放性类似,允许对存储系统实施动态的升级、扩展,接入第三方存储服务或设备等。
作为软件定义的存储的核心技术,我们先聚焦存储虚拟化,它可以在计算、网络和存储层实施。
·在计算层,虚拟机管理程序为虚拟机分配存储空间,而屏蔽掉了(不暴露)物理存储的复杂性。
· 数据块(Block)和文件级别(File)的虚拟化是基于网络的虚拟化技术。这两项技术在网络层中嵌入虚拟化存储资源的智能,我们常见的NFS/CIFS网络协议正是这些存储虚拟化技术在网络层面的体现。
事实上数据块与文件类型的存储从操作系统技术栈角度看通常是在不同层实现的。以Linux操作系统为例,如下图所示,文件系统通常在块设备之上实现(每多一层抽象、虚拟化,效率就会降低一点),这也解释了为什么通常基于块设备的解决方案的效率(数据吞吐率)高于基于文件系统。
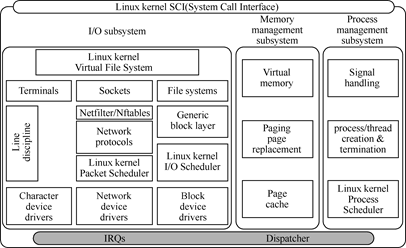
图:Linux内核系统调用接口
· 在存储层,虚拟资源调配和自动存储分层一起简化存储管理,并帮助优化存储基础架构(见下图)。
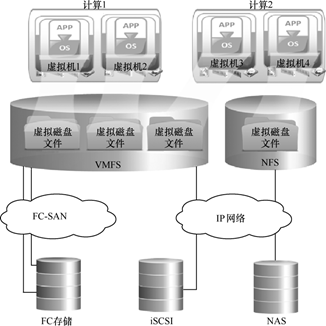
图:虚拟化的存储
下面我们以虚拟机为例介绍一下虚拟化计算、存储与网络如何整合工作。
虚拟机通常是作为一组文件存储在分配给虚拟机管理程序的存储设备上。其中一个名为“虚拟磁盘文件”的文件表示虚拟机用来存储其数据的虚拟磁盘。虚拟磁盘对于虚拟机显示为本地物理磁盘驱动器。虚拟磁盘文件的大小表示分配给虚拟磁盘的存储空间。虚拟机管理程序可以访问光纤通道存储设备或IP存储设备,例如iSCSI和网络连接存储设备。虚拟机一直察觉不到可用于虚拟机管理程序的总存储空间和底层存储技术。虚拟机文件可以由虚拟机管理程序的本机文件系统[也被称为虚拟机文件系统 (VMFS)]或网络文件系统 (NFS)(如网络连接存储文件系统)来管理。
主流的软件定义存储技术方案通常对数据管理(Control Plane)与数据读写(Data Plane)实现分离,由统一的管理接口与上层管理软件交互,而在数据交互方面,则可以兼容各种不同的连接方式。这种方式可以很好地与传统的软硬件环境兼容,从而避免“破坏性”的改造。如何合理利用各级存储资源,在数据中心的级别上提供分层、缓存也是需要特别考虑的。因此,软件定义存储中的控制层通常提供如::系统配置、自动化、自服务、管控中心等服务,而在数据层则暴露给应用不同类型的存储服务,如对象存储、HDFS、文件或块存储。整个SDS系统逻辑组件可参考下图所示。
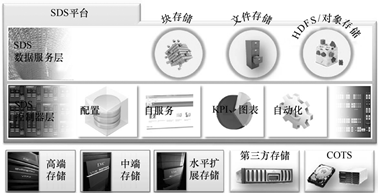
图:软件定义存储的逻辑组件与分层
软件定义的存储将抽象的控制层与数据层进行了分离,并提供接口给用户。用户可以使用接口定义自己的数据控制策略。为什么要将抽象的控制层与数据层分离,并且提供接口给用户调用?如表3-5所示,控制层是指对数据的管理策略,控制层不需要知道数据具体的存储方式,如块、文件或者对象存储。控制层的时间损耗(延迟)级别是在毫秒级。数据层则是指具体读写硬件方式,如块、文件或者对象读。时间延迟是在微秒级。
存储控制层和数据层(下表):
| 存储控制层 | 存储数据层 | |
| 速度级别 | 毫秒级 | 微秒级 |
| 例子 | 数据服务的策略 | Block、NAS、Object I/O |
| 表示 | 数据服务策略 | 数据服务特性 |
用户在使用存储时,着重关注数据服务的策略,而这些策略与具体的数据存储方式无关。当今的存储虚拟化产品将存储控制和数据层结合,即数据服务的策略紧密依赖于数据存储的方式。事实上,数据存储速度是微秒级,而数据存储控制较慢。当实现数据服务策略时,主要的时间开销在控制层,而传统的存储虚拟化技术不能灵活配置存储控制,因此针对某个服务的变化,响应时间主要是控制开销。再者,用户存储数据时,必须对数据的控制和存储方式都需要足够的了解,这增加了使用存储资源的难度,而且存储资源的可扩展性不高。此外,由于传统的存储虚拟化技术缺少标准的存储数据监控功能,当某个设备出现问题时,用户只能依赖底层的一些存储机制(如日志)进行问题发现和定位。表3-6中描述了存储虚拟化与软件定义的存储之间的异同。
存储虚拟化与软件定义的存储(下表):
| 存储虚拟化 | 软件定义的存储 | |
| Control Plane | 抽象 | 抽象 |
| Data Plane | 抽象 | 不抽象 |
| 隔离性要求 | 高 | 低 |
| 时间开销 | 高 | 低 |
| 可扩展性 | 低 | 高 |
| 数据监控 | 低 | 高 |
| 数据安全 | 低 | 高 |
从软件定义的数据中心角度看,软件定义存储形成了一个统一的虚拟存储池(Unified Virtualized Storage Pool),该存储池提供了标准化接口的存储应用服务,例如典型的企业级Exchange(邮件)、Hadoop(大数据分析)、VDI(远程桌面、瘦客户端后台)、数据库等存储服务。这些服务的等级、特性、优先级等可以通过软件定义数据中心的SLA等策略来规范与定制。图3-35形象地展示了软件定义存储与软件定义数据中心的逻辑关系。
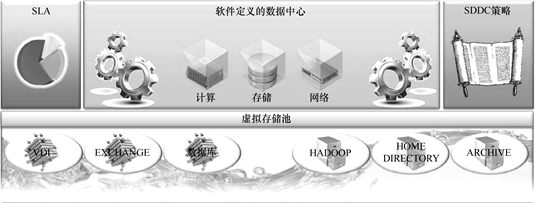
图:软件定义的数据中心之软件定义的存储
换一个角度,从技术栈视角去看软件定义的存储、网络与计算,结合曾经流行的OpenStack平台组件(或者K8S...),我们可以把一个软件定义的数据中心从功能上分为四层(自下而上,如图3-36所示):
· 基础架构层
·云管理层
· 云服务层
·管理界面层
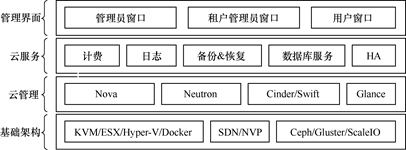
图:软件定义的数据中心之软件定义的存储(技术栈角度)
基础架构层由典型的计算虚拟化组件(KVM/Docker等)、网络虚拟化(NVP/OpenFlow/Open vSwitch等)以及存储虚拟化(Ceph/ScaleIO/VSAN等)构成;云管理层则可视为对基础架构层的封装、标准化并向上层提供统一可编程与管理接口;云服务层向之上的管理界面提供了标准化服务接口,如计费、日志、数据库服务、数据备份与恢复等服务。
上图中的软件定义数据中心依旧缺失了另外两块主要的组件:
·Security(安全组件)
·M&O(Management & Orchestration)管理与编排组件
随着数据中心系统的规模与复杂度指数级地提高,管理这样一个庞大的系统需要高度的自动化以及与之匹配的安全保障。因此,对硬件与软件的综合管理与编排以及安全管理系统变得越来越重要,例如VMware的vCenter、微软的System Center、开源OpenStack项目都提供了各自的SDDC M&O组件。安全组件则通常会以系统安全分析、入侵预防与报警、漏洞检测、事件流分析等功能组件形式与M&O系统对接。图3-37展示了在软件定义的数据中心中,五大组件(软件定义的计算、存储、网络、安全及M&O)的逻辑、分层关系。
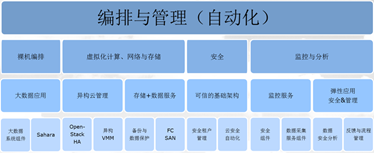
图:软件定义的数据中心五大组件逻辑架构图
需要指出的是无论是安全还是M&O,它们整体的发展趋势都是朝着大数据、快数据、流数据的方向发展,相关系统的体系架构也一定是朝着分布式、并行式的云计算架构方向前进,这其中对网络(负责数据的迁移)、计算(负责通过对数据的计算、分析得出信息与智能)以及存储(负责数据最终的存放与管理)具有天然的需求。因此,我们在看待其中任何一个环节、部件或组件的时候,都需要有一个五位一体(见上图)的全局观,这样才能避免片面、孤立或过度微观。
另据IDC 2015年提供的报告,未来企业级存储变革的四大关键技术分别是:闪存、软件定义、融合存储和云。闪存与融合存储指的都是硬件层面设备的迭代更新,而软件定义与云则是通过软件化、虚拟化(抽象化)来更好地把硬件接入到云化的软件系统架构内,以更好地服务于用户需求。今天看来,这份6年前报告依然是有价值的,不过有一些新的变化。闪存,特别是企业级闪存,显然需要更激进的替代现有的仍旧基于磁盘的存储模式,随着闪存的成本不断降低,闪存存储所带来的10倍以上的性能优势不言而喻,特别是对于数据库级别的产品而言,脱离了底层的硬件性能提升而谈软件定义存储,未免显得舍本逐末了。另外,最近1-2年随着大内存(持久化内存)产品的推出(例如Intel的Optane),笔者以为,这将会是颠覆性的 -- 没有人可以拒绝内存级别的持久化存储产品,想想数据库如果持久化在内存级存储设备上面,没有IOPS的世界会是什么样子的?光速对高铁、高铁对蜗牛的感觉?
让我们把剩下的交给时光和人心。













![[转]勒贝格积分的框架与通俗理解](http://data.artofproblemsolving.com/images/latex/e/0/1/e0184adedf913b076626646d3f52c3b49c39ad6d.gif)

