红黑树原理详解及代码实现

article/2025/11/3 7:57:58

文章目录

  • 1. 红黑树概念
  • 2. 节点定义
  • 3. 旋转操作
  • 4. 插入操作
  • 5. 删除操作
  • 6. 完整代码

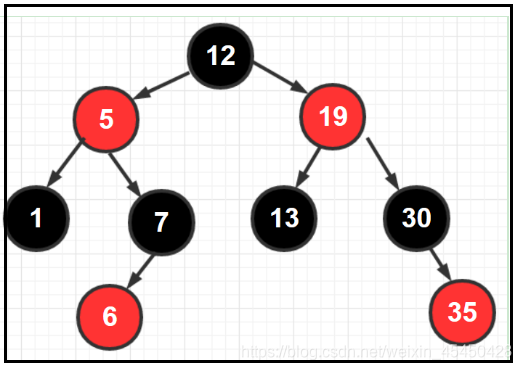
1. 红黑树概念

在这里插入图片描述
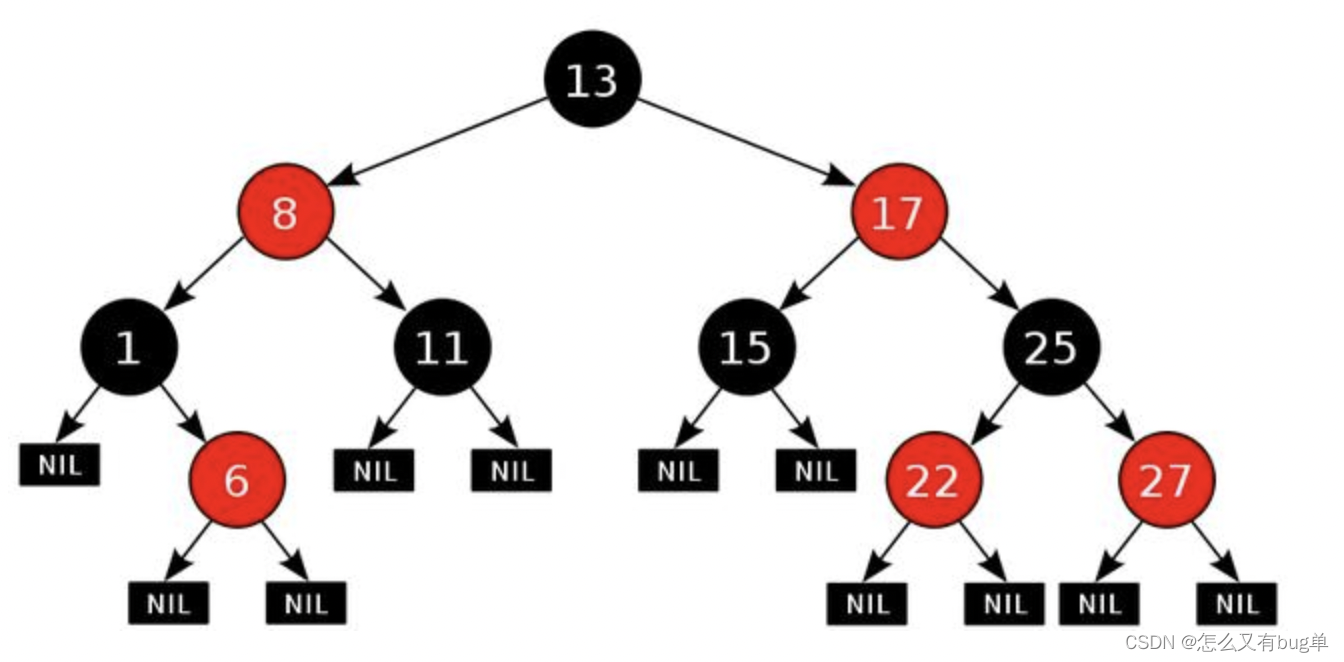
下图就是一棵红黑树：
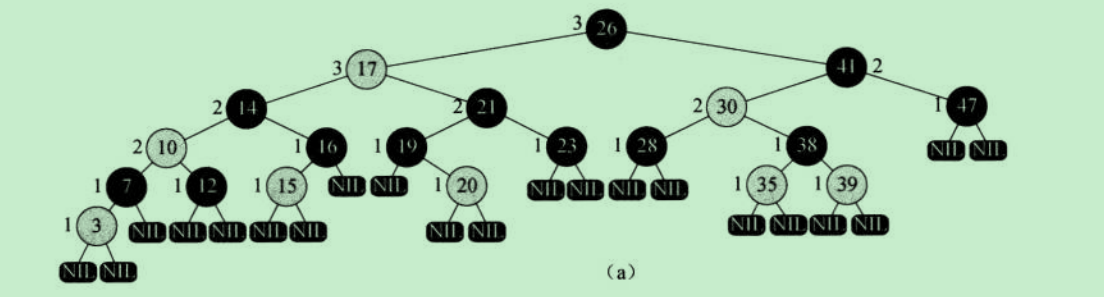
在这里插入图片描述

为了后续操作中不出现空指针异常，可以加入一个额外的哨兵节点T，T作为所有叶子节点的子节点，作为根节点的父节点，节点T要求是黑色，其他属性不做要求，如下图所示：
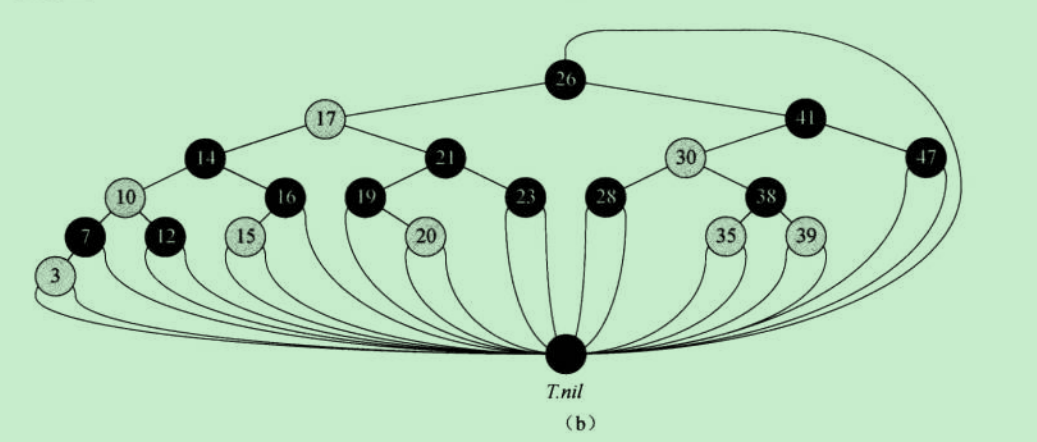
在这里插入图片描述

2. 节点定义

class Node {int key;Node left, right;Node parent;boolean color;public Node(boolean color) {super();this.color = color;}public Node(int key) {super();this.key = key;}@Overridepublic String toString() {return "Node [key=" + key + ", color=" + color + " p=" + parent.key + "]";}}

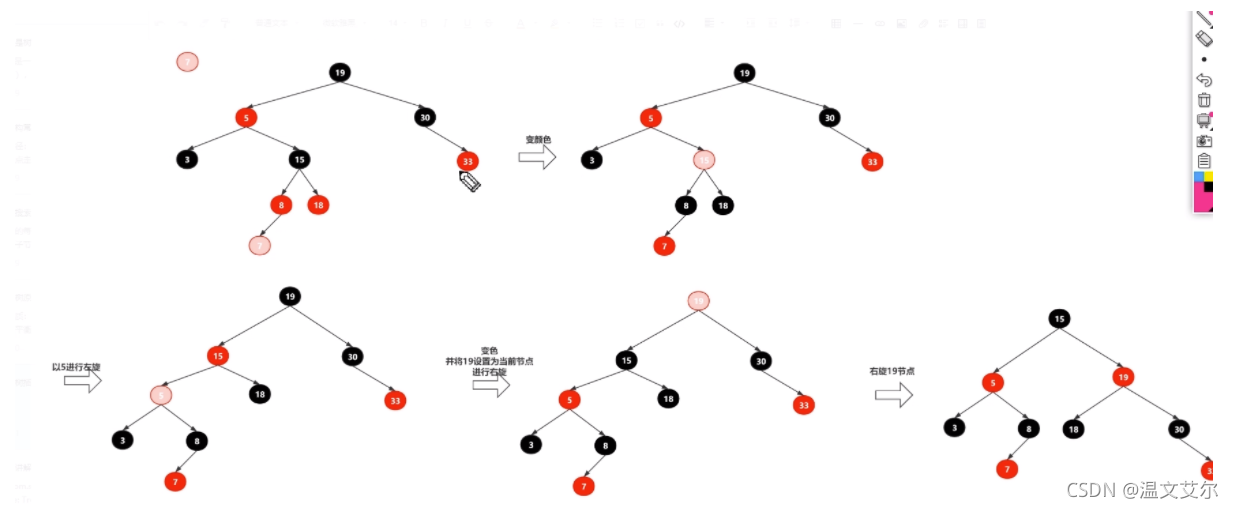
3. 旋转操作

在这里插入图片描述

左旋操作代码：

public void rotateLeft(Node x) {Node y = x.right;x.right = y.left;// y的左子树作为x的右子树if (y.left != nil) {// y存在左子树y.left.parent = x;// 该左子树的父节点变为x}y.parent = x.parent;// x之前的父节点现在成为y的父节点if (x.parent == nil) {// x是根节点root = y;// y替代x成为根节点} else if (x == x.parent.left) {// x是左子节点x.parent.left = y;// y替代x作为左子节点} else {// x是右子节点x.parent.right = y;// y替代x作为右子节点}y.left = x;// x作为y的左子节点x.parent = y;// y作为x的父节点}

右旋操作代码：

public void rotateRight(Node y) {Node x = y.left;y.left = x.right;if (x.right != null) {// x存在右子树x.right.parent = y;// x的右子树的父节点变为y}x.parent = y.parent;// y之前的父节点现在变为x的父节点if (y == nil) {// y是根节点root = x;// x替代y成为根节点} else if (y == y.parent.left) {// y是左子节点y.parent.left = x;// x代替y作为其父节点的左子节点} else {// y是右子节点y.parent.right = x;// x代替y作为其父节点的右子节点}x.right = y;// y变成x的右子节点y.parent = x;// x变成y的父节点}

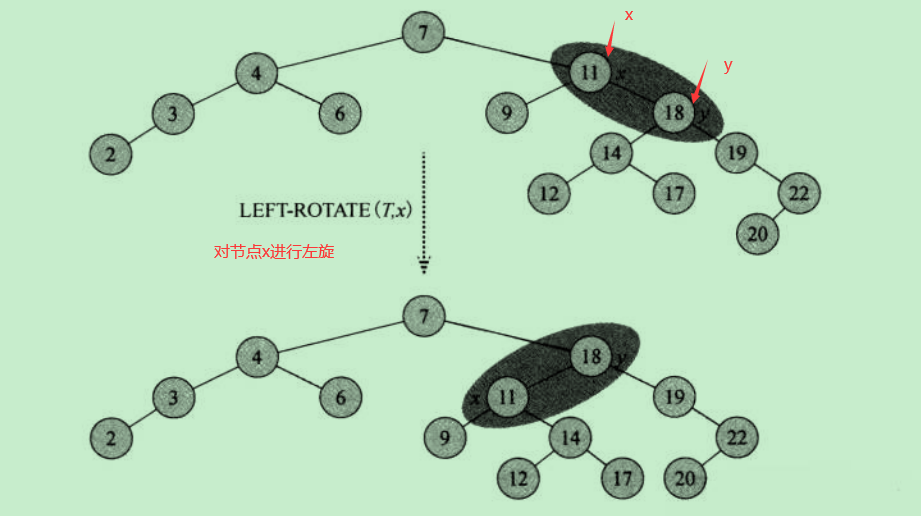
在这里插入图片描述

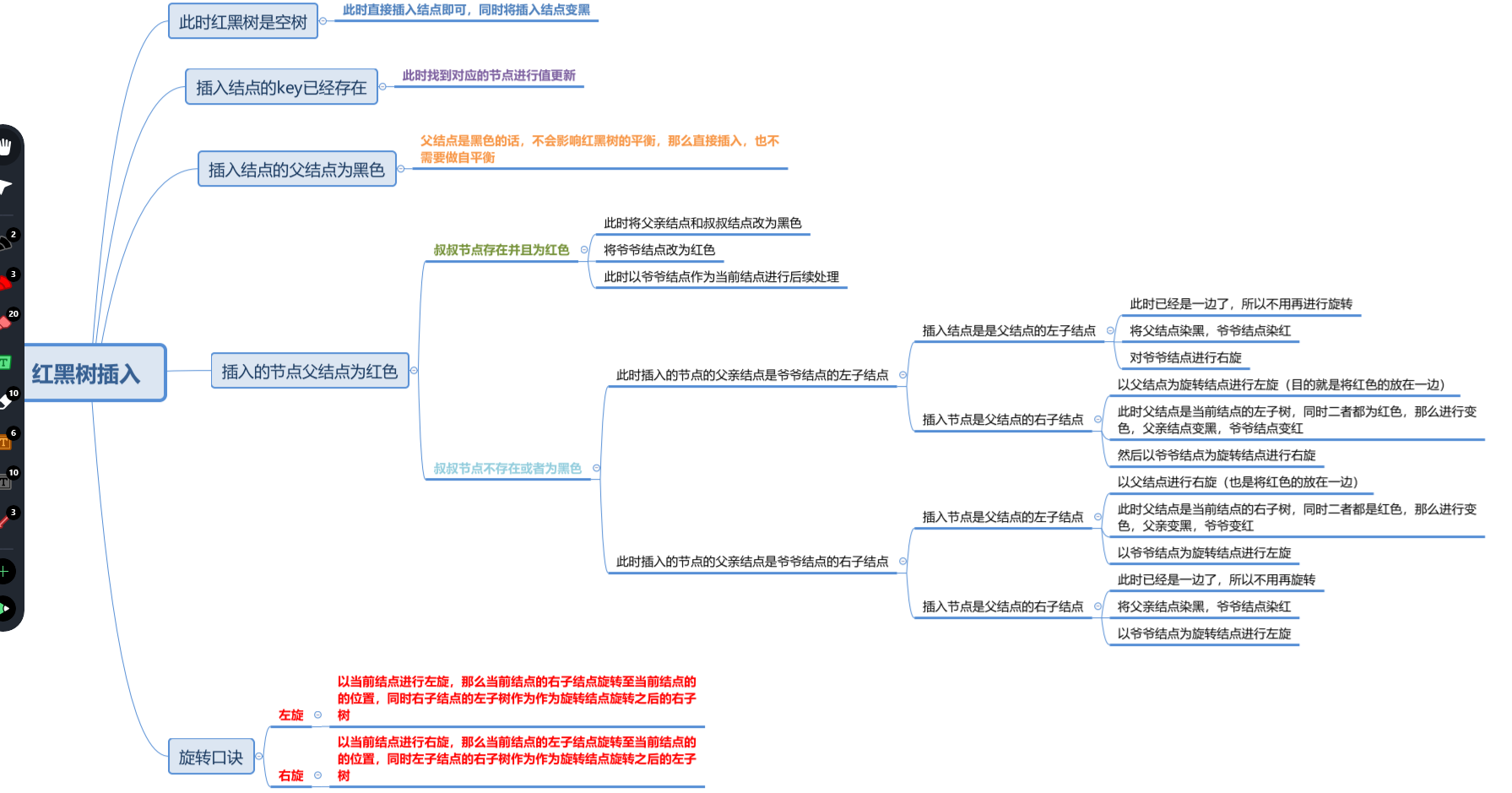
4. 插入操作

public void insert(Node z) {Node y = nil;// y指向哨兵节点Node x = root;// x指向根节点while (x != nil) {y = x;// y保存更新前的xif (z.key < x.key) {// z的key较小 然后去x左子树中查找x = x.left;} else {// z的key较大 然后去x右子树中查找x = x.right;}}z.parent = y;// y作为z的父节点if (y == nil) {// 说明目前树为空 插入的是第一个节点root = z;// z成为根节点} else if (z.key < y.key) {y.left = z;// z的值比父节点值小 作为左子节点} else {y.right = z;// z的值比父节点值大 作为右子节点}z.left = nil;z.right = nil;// z是叶子节点z.color = RED;// 叶子节点红色insetFix(z);// 插入之后需要调整树的结构}

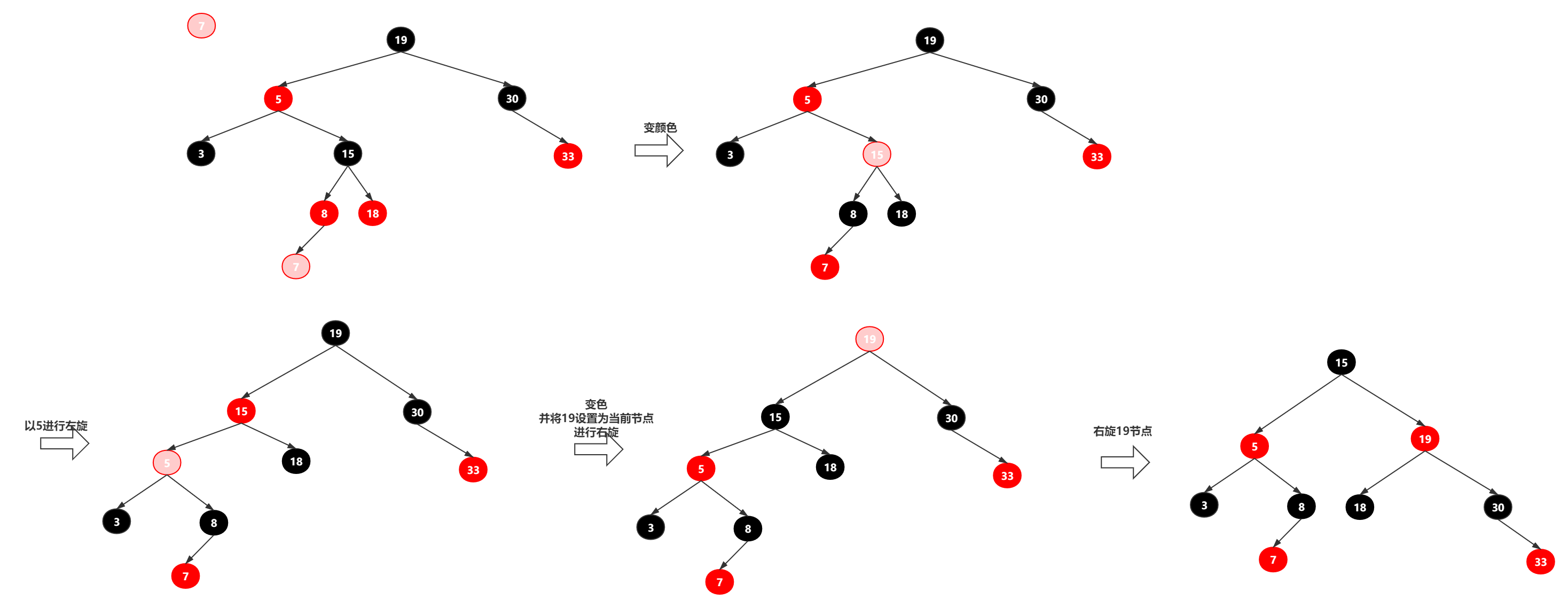
插入操作完成了还需要进行树的结构调整，先来看下面几种情况：

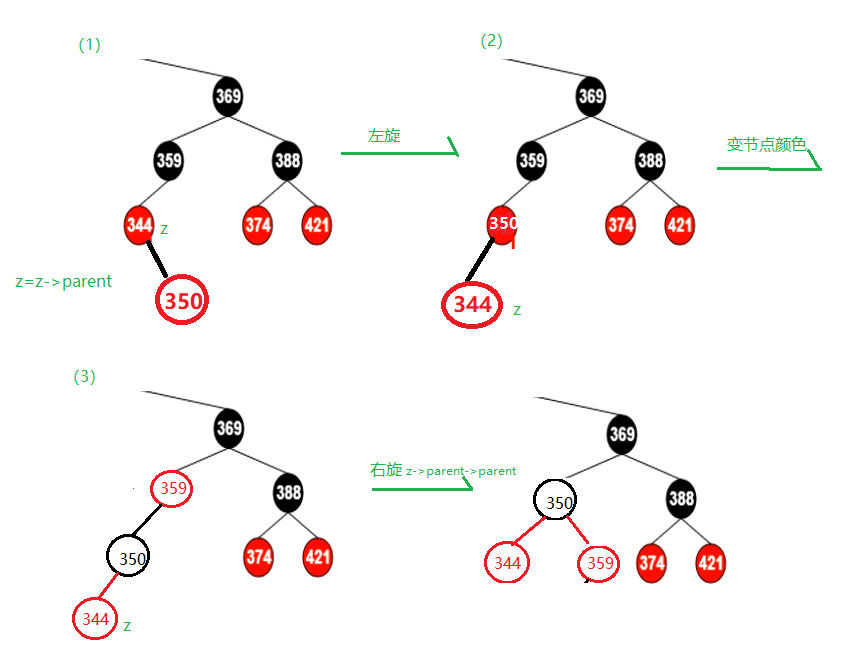
情况1: 新插入节点z的叔节点y是红色的
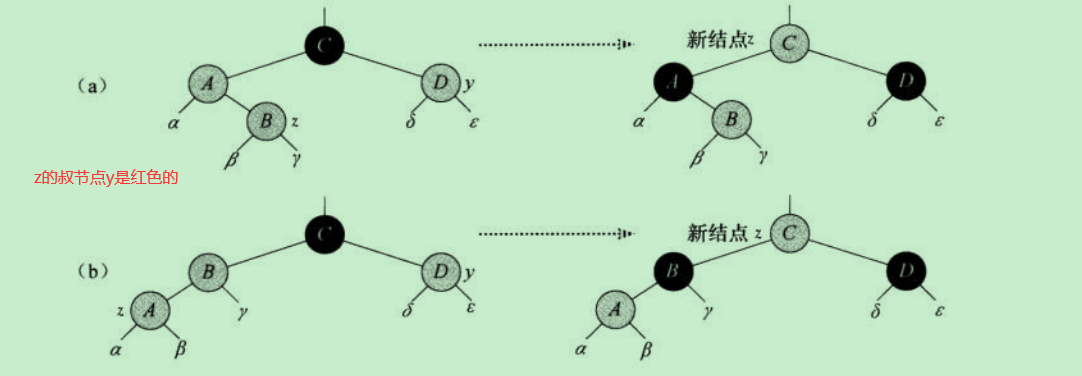
在这里插入图片描述

上图中的（a)或(b)违反了性质：一个红节点的两个子节点都是黑色的
解决方案：z的父节点和树节点颜色由红变黑，z的爷爷节点颜色由黑变红

				Node y=z.parent.parent.right;if(y.color==RED) {z.parent.color=BLACK;y.color=BLACK;z.parent.parent.color=RED;z=z.parent.parent;//z指向爷爷节点继续处理树的结构}

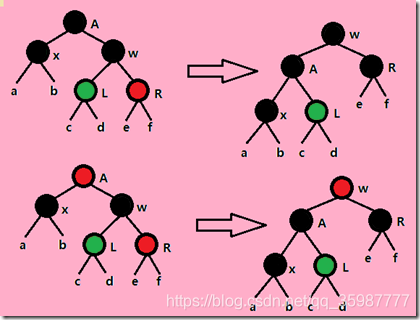
情况2: 新插入节点z的叔节点y是黑色的并且z是一个右孩子节点
情况3: 新插入节点z的叔节点y是黑色的并且z是一个左孩子节点
情况2和情况3可以放在一张图中来讨论，因为情况2可以通过左旋操作进入情况3，入下图所示：
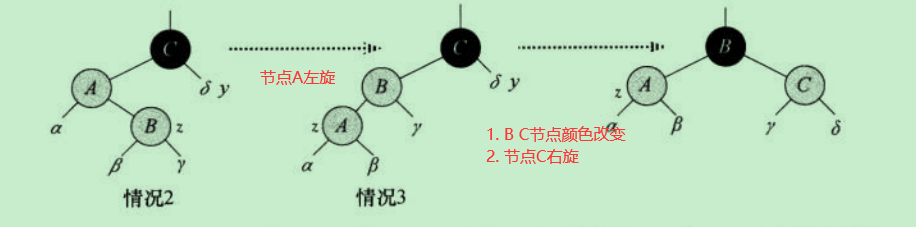
在这里插入图片描述

			else if(z==z.parent.right) {//情况2z=z.parent;rotateLeft(z);z.parent.color=BLACK;z.parent.parent.color=RED;rotateRight(z.parent.parent);}else if(z==z.parent.right) {//情况3z.parent.color=BLACK;z.parent.parent.color=RED;rotateRight(z.parent.parent);}

上面的三种情况都是基于新插入节点z的父节点是一个左子节点的情形，对于z的父节点是一个右子节点的情况也有三种，与上面三种情况对称，关于调整的完整代码如下：

public void insetFix(Node z) {while (z.parent.color == RED) {if (z.parent == z.parent.parent.left) {// z的父节点是左子节点Node y = z.parent.parent.right;if (y != nil && y.color == RED) {// 情况1z.parent.color = BLACK;y.color = BLACK;z.parent.parent.color = RED;z = z.parent.parent;continue;} else if (z == z.parent.right) {// 情况2z = z.parent;rotateLeft(z);}// 情况3z.parent.color = BLACK;z.parent.parent.color = RED;rotateRight(z.parent.parent);} else if (z.parent == z.parent.parent.right) {// z的父节点是右子节点Node y = z.parent.parent.left;if (y != nil && y.color == RED) {z.parent.color = BLACK;y.color = BLACK;z.parent.parent.color = RED;z = z.parent.parent;continue;} else if (z == z.parent.left) {z = z.parent;rotateRight(z);}z.parent.color = BLACK;z.parent.parent.color = RED;rotateLeft(z.parent.parent);}root.color = BLACK;}}

5. 删除操作

红黑树的删除操作和BST的删除操作类似，如果待删除节点x没有左子节点，就用右子节点替代x;如果待删除节点x没有右子节点，就用左子节点替代x; 如果x既有左子节点也有右子节点，可以使用x右子树中的最小节点y来替代x, y之前的右子树来替换y, x的右子树作为y新的右子树，只不过在红黑树中需要根据节点的颜色进行树结构的调整

// 用节点v 替代 节点upublic void transplant(Node u, Node v) {if (u.parent == T) {// u是根节点T.left = v;// v替代u作为根节点} else if (u == u.parent.left) {// u是左子节点u.parent.left = v;} else if (u == u.parent.right) {u.parent.right = v;}v.parent = u.parent;// u的父节点成为v的父节点}public void delete(Node z) {//z是待删除节点Node y = z;Node x = null;boolean originColor = y.color;if (z.left == T) {// z没有左子节点x = z.right;transplant(z, z.right);//z的右子节点替代z} else if (z.right == T) {//z没有右子节点x = z.left;transplant(z, z.left);//z的左子节点替代z}else {//z的左右子节点都存在y=minimum(z.right);//y保存z右子树中的最小节点 用y替换zoriginColor=y.color;x=y.right;if(y.parent==z) {//y是z的直接右子节点 不需要else语句中的y的右子树替换yx.parent=y;}else {transplant(y, y.right);//y的右子树替换yy.right=z.right;//待删除节点z的右子树成为y的右子树y.right.parent=y;//更新y的右子树的的父节点}transplant(z, y);//用y替换zy.left=z.left;//z的左子树作为y的左子树y.left.parent=y;y.color=z.color;//更新颜色}if(originColor==BLACK) {//待删除节点的颜色是黑色 需要调整树的结构deleteFix(x);}}/** 寻找某个子树中的最小节点*/Node minimum(Node subTreeRoot) {while (subTreeRoot.left != T) {subTreeRoot = subTreeRoot.left;}return subTreeRoot;}

删除-调整操作：

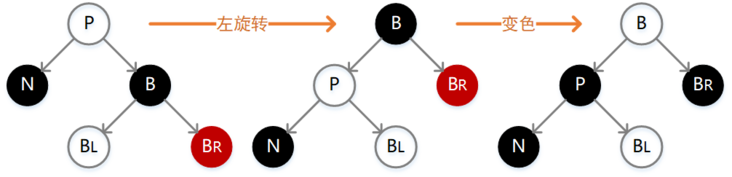
情形1：待调整节点x的兄弟节点w是红色
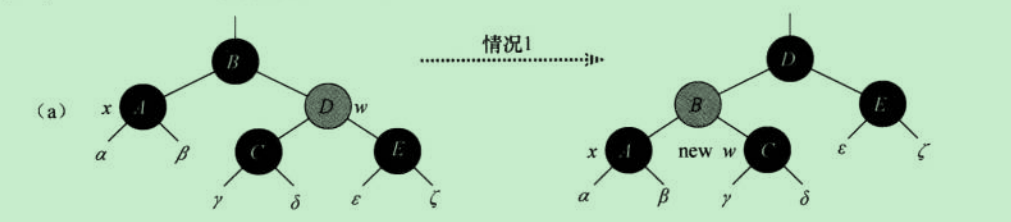
在这里插入图片描述

					w.color=BLACK;x.parent.color=RED;rotateLeft(x.parent);w=x.parent.right;

情形2：待调整节点x的兄弟节点w是黑色的，并且w的两个子节点也是黑色的
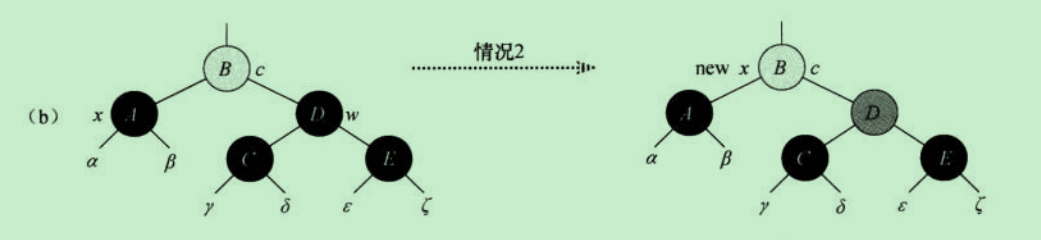
在这里插入图片描述

					w.color=RED;x=x.parent;continue;

情形3：待调整节点x的兄弟节点w是黑色的，w的左子节点为红色，右子节点为黑色
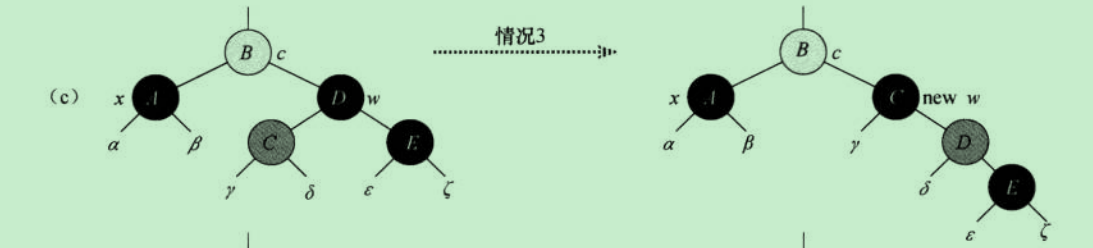
在这里插入图片描述

					w.left.color=BLACK;w.color=RED;rotateRight(w);w=x.parent.right;

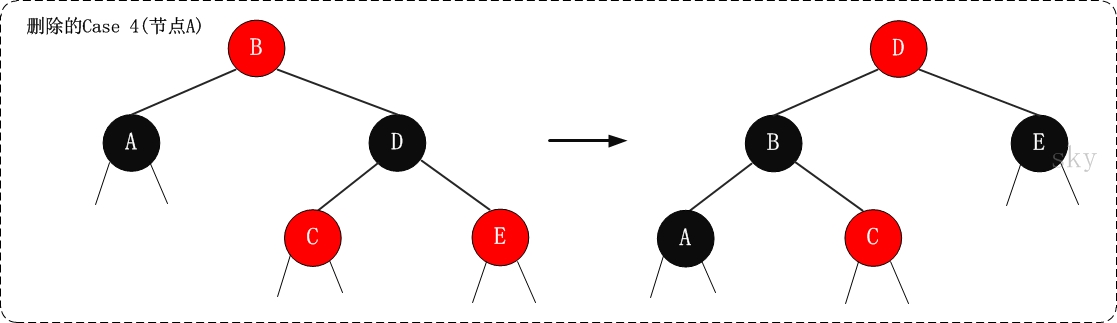
情形4：待调整节点x的兄弟节点w是黑色的，w的右子节点为红色，左子节点不考虑
在这里插入图片描述

				w.color=x.parent.color;//case4x.parent.color=BLACK;w.right.color=BLACK;rotateLeft(x.parent);x=T.left;

可以发现情况1经过转化可以变成情况2，3，4中的一种，情况3经过转化后就变成了情况4

上面的4种情况是基于x是左子节点的情况，对于x是右子节点的情况，只一将上面代码中的left和right互换即可

刪除-调整代码如下：

public void deleteFix(Node x) {Node w = null;while (x != root && x.color == BLACK) {if (x == x.parent.left) {w = x.parent.right;if (w.color == RED) {// case1w.color = BLACK;x.parent.color = RED;rotateLeft(x.parent);w = x.parent.right;}if (w.left.color == BLACK && w.right.color == BLACK) {// case2w.color = RED;x = x.parent;continue;} else if (w.right.color == BLACK) {// case3w.left.color = BLACK;w.color = RED;rotateRight(w);w = x.parent.right;}w.color = x.parent.color;// case4x.parent.color = BLACK;w.right.color = BLACK;rotateLeft(x.parent);x = root;} else {w = x.parent.left;if (w.color == RED) {// case1w.color = BLACK;x.parent.color = RED;rotateRight(w);w = x.parent.left;}if (w.left.color == BLACK && w.right.color == BLACK) {// case2w.color = RED;x = x.parent;continue;} else if (w.right.color == BLACK) {// case3w.right.color = BLACK;w.color = RED;rotateLeft(w);w = x.parent.left;}w.color = x.parent.color;// case4x.parent.color = BLACK;w.left.color = BLACK;rotateRight(x.parent);x = root;}}x.color = BLACK;}

6. 完整代码

package datastructure.tree;import java.util.LinkedList;
import java.util.Queue;class Node {int key;Node left, right;Node parent;boolean color;public Node(boolean color) {super();this.color = color;}public Node(int key) {super();this.key = key;}@Overridepublic String toString() {return "Node [key=" + key + ", color=" + color + " p=" + parent.key + "]";}}public class RedBlackTree {private static final boolean RED = true;private static final boolean BLACK = false;private Node nil;private Node root;/** 初始化操作中创建一个哨兵节点nil root开始等于nil*/public RedBlackTree() {nil = new Node(BLACK);nil.key = -1;root = nil;}public void rotateLeft(Node x) {Node y = x.right;x.right = y.left;// y的左子树作为x的右子树if (y.left != nil) {// y存在左子树y.left.parent = x;// 该左子树的父节点变为x}y.parent = x.parent;// x之前的父节点现在成为y的父节点if (x.parent == nil) {// x是根节点root = y;// y替代x成为根节点} else if (x == x.parent.left) {// x是左子节点x.parent.left = y;// y替代x作为左子节点} else {// x是右子节点x.parent.right = y;// y替代x作为右子节点}y.left = x;// x作为y的左子节点x.parent = y;// y作为x的父节点}public void rotateRight(Node y) {Node x = y.left;y.left = x.right;if (x.right != null) {// x存在右子树x.right.parent = y;// x的右子树的父节点变为y}x.parent = y.parent;// y之前的父节点现在变为x的父节点if (y == nil) {// y是根节点root = x;// x替代y成为根节点} else if (y == y.parent.left) {// y是左子节点y.parent.left = x;// x代替y作为其父节点的左子节点} else {// y是右子节点y.parent.right = x;// x代替y作为其父节点的右子节点}x.right = y;// y变成x的右子节点y.parent = x;// x变成y的父节点}public void insert(Node z) {Node y = nil;// y指向哨兵节点Node x = root;// x指向根节点while (x != nil) {y = x;// y保存更新前的xif (z.key < x.key) {// z的key较小 然后去x左子树中查找x = x.left;} else {// z的key较大 然后去x右子树中查找x = x.right;}}z.parent = y;// y作为z的父节点if (y == nil) {// 说明目前树为空 插入的是第一个节点root = z;// z成为根节点} else if (z.key < y.key) {y.left = z;// z的值比父节点值小 作为左子节点} else {y.right = z;// z的值比父节点值大 作为右子节点}z.left = nil;z.right = nil;// z是叶子节点z.color = RED;// 叶子节点红色insetFix(z);// 插入之后需要调整树的结构}public void insetFix(Node z) {while (z.parent.color == RED) {if (z.parent == z.parent.parent.left) {// z的父节点是左子节点Node y = z.parent.parent.right;if (y != nil && y.color == RED) {// 情况1z.parent.color = BLACK;y.color = BLACK;z.parent.parent.color = RED;z = z.parent.parent;continue;} else if (z == z.parent.right) {// 情况2z = z.parent;rotateLeft(z);}//情况2经过调整之后可以变成情况3// 情况3z.parent.color = BLACK;z.parent.parent.color = RED;rotateRight(z.parent.parent);} else if (z.parent == z.parent.parent.right) {// z的父节点是右子节点Node y = z.parent.parent.left;if (y != nil && y.color == RED) {z.parent.color = BLACK;y.color = BLACK;z.parent.parent.color = RED;z = z.parent.parent;continue;} else if (z == z.parent.left) {z = z.parent;rotateRight(z);}z.parent.color = BLACK;z.parent.parent.color = RED;rotateLeft(z.parent.parent);}root.color = BLACK;}}// 用节点v 替代 节点upublic void transplant(Node u, Node v) {if (u.parent == nil) {// u是根节点root = v;// v替代u作为根节点} else if (u == u.parent.left) {// u是左子节点u.parent.left = v;} else if (u == u.parent.right) {u.parent.right = v;}v.parent = u.parent;// u的父节点成为v的父节点}public void delete(Node z) {Node y = z;Node x = null;boolean originColor = y.color;if (z.left == nil) {// z没有左子节点x = z.right;transplant(z, z.right);// z的右子节点替代z} else if (z.right == nil) {// z没有右子节点x = z.left;transplant(z, z.left);// z的左子节点替代z} else {// z的左右子节点都存在y = minimum(z.right);// y保存z右子树中的最小节点 用y替换zoriginColor = y.color;x = y.right;if (y.parent == z) {// y是z的直接右子节点 不需要else语句中的y的右子树替换yx.parent = y;} else {transplant(y, y.right);// y的右子树替换yy.right = z.right;// 待删除节点z的右子树成为y的右子树y.right.parent = y;// 更新y的右子树的的父节点}transplant(z, y);// 用y替换zy.left = z.left;y.left.parent = y;y.color = z.color;}if (originColor == BLACK) {// 节点y的颜色是黑色 需要调整树的结构deleteFix(x);}}/** 寻找某个子树中的最小节点*/Node minimum(Node subTreeRoot) {while (subTreeRoot.left != nil) {subTreeRoot = subTreeRoot.left;}return subTreeRoot;}public void deleteFix(Node x) {Node w = null;while (x != root && x.color == BLACK) {if (x == x.parent.left) {w = x.parent.right;if (w.color == RED) {// case1w.color = BLACK;x.parent.color = RED;rotateLeft(x.parent);w = x.parent.right;}if (w.left.color == BLACK && w.right.color == BLACK) {// case2w.color = RED;x = x.parent;continue;} else if (w.right.color == BLACK) {// case3w.left.color = BLACK;w.color = RED;rotateRight(w);w = x.parent.right;}//case3 经过调整之后可以变成case4w.color = x.parent.color;// case4x.parent.color = BLACK;w.right.color = BLACK;rotateLeft(x.parent);x = root;} else {w = x.parent.left;if (w.color == RED) {// case1w.color = BLACK;x.parent.color = RED;rotateRight(w);w = x.parent.left;}if (w.left.color == BLACK && w.right.color == BLACK) {// case2w.color = RED;x = x.parent;continue;} else if (w.right.color == BLACK) {// case3w.right.color = BLACK;w.color = RED;rotateLeft(w);w = x.parent.left;}w.color = x.parent.color;// case4x.parent.color = BLACK;w.left.color = BLACK;rotateRight(x.parent);x = root;}}x.color = BLACK;}/** 层次遍历*/public void printTreeByLevel(Node root) {Queue<Node> q = new LinkedList<>();q.offer(root);while (!q.isEmpty()) {int sz = q.size();Node node = null;for (int i = 0; i < sz; i++) {node = q.poll();System.out.print(node + " ");if (node.left != nil)q.offer(node.left);if (node.right != nil)q.offer(node.right);}System.out.println();}}/** 根据key查找某个节点*/public Node find(Node root, int key) {if (root == nil) {return null;}if (root.key < key) {return find(root.right, key);} else if (root.key > key) {return find(root.left, key);} else if (key == root.key) {return root;}return null;}/** 中序遍历*/public void printInorder(Node root) {if (root == nil)return;printInorder(root.left);System.out.println(root);printInorder(root.right);}public static void main(String[] args) {RedBlackTree tree = new RedBlackTree();System.out.println("插入数据:");for (int i = 1; i <= 10; i++) {tree.insert(new Node(i));}System.out.println("层次遍历：");tree.printTreeByLevel(tree.root);System.out.println("中序遍历:");tree.printInorder(tree.root);System.out.println("删除数据:");int[] delete = { 1, 2,3, 4,5, 6,7,8, 9,10 };for (int num : delete) {Node delNode = tree.find(tree.root, num);System.out.println("删除了元素" + delNode);tree.delete(delNode);System.out.println("中序遍历:");tree.printInorder(tree.root);}}
}

http://chatgpt.dhexx.cn/article/CeLr79q7.shtml

相关文章

快速理解红黑树原理

快速理解红黑树原理

快速理解红黑树原理 红黑树 简介 红黑树 其实就是一个二叉树。 1.0 常用的二叉树类型 简单说二叉树概念&#xff1a; 二叉树 又称度为至多二的树。 1.1 平衡二叉树 平衡二叉树又称 AVL 树 特点&#xff1a;一个根节点的左右个子树的高度差不超过1 平衡二叉树 非平衡二叉树…
阅读更多...
数据结构-红黑树原理分析

数据结构-红黑树原理分析

前言 在阅读HashMap源码的时候发现&#xff0c;java1.8的HashMap的链表实现增加了红黑树&#xff0c;当链表长度超过指定阈值8的时候回进行树化。 为了提高增删查的效率。 而红黑树又比较复杂&#xff0c;所以专门写一篇关于红黑树的文章。 概念 R-B Tree&#xff0c;全称是…
阅读更多...
红黑树原理剖析

红黑树原理剖析

首先介绍一下红黑树的几点性质: 性质1:根节点是黑色 性质2:每个叶子节点是黑色(指的是空叶子节点) 性质3:每个红色节点的两个子节点一定是黑色 (子节点必须同时存在或不存在) 性质4:任意一节点到每个叶子节点的路径都包含数量相同的黑节点(非空叶子…
阅读更多...
红黑树原理及插入

红黑树原理及插入

文章目录 1、前言2、红黑树2.1、性质2.2、操作2.2.1、变色2.2.2、左旋2.2.3、右旋2.2.4、查找2.2.5、插入 2.3、插入情景2.3.1、红黑树为空树2.3.2、插入结点的Key已存在2.3.3、插入结点的父结点为黑结点2.3.4、插入节点的父节点为红色2.3.4.1、叔叔结点存在并且为红结点 2.3.5…
阅读更多...
红黑树原理及代码实现（一）

红黑树原理及代码实现（一）

红黑树简介 红黑树是一种自平衡的二叉查找树&#xff0c;它的统计性能要优于平衡二叉树&#xff0c;因此在很多地方都有应用&#xff0c;例如Java中的TreeMap&#xff0c;HashMap等数据结构都使用到了红黑树。红黑树对很多人来说熟悉而陌生&#xff0c;熟悉则是因为知道红黑树…
阅读更多...
图解红黑树原理

图解红黑树原理

一.红黑树的性质&#xff08;一种自平衡的二叉查找树&#xff09; 1. 根节点是黑色。 2. 节点是红色或黑色 3. 叶子节点都是黑色的空节点&#xff08;NIL节点&#xff09; 意思就是末尾一排是黑色空节点&#xff08;可全部省略&#xff09; &#xff08;叶子节点意思是没有子…
阅读更多...
红黑树原理和算法详细介绍

红黑树原理和算法详细介绍

目录 1 R-B Tree简介 2 红黑树的时间复杂度和相关证明 3 红黑树的基本操作 1. 左旋 2. 右旋 3. 添加 4.1 删除 1 R-B Tree简介 R-B Tree&#xff0c;全称是Red-Black Tree&#xff0c;又称为“红黑树”&#xff0c;它一种特殊的二叉查找树。红黑树的每个节点上都有存储…
阅读更多...
HashMap底层红黑树原理（超详细图解）+手写红黑树代码

HashMap底层红黑树原理（超详细图解）+手写红黑树代码

在看完了小刘老师和黑马的源码视频之后,我整理了一篇HashMap的底层源码文章&#xff0c;学海无涯&#xff0c;这几天看了对红黑树的讲解&#xff0c;故将其整理出来 HashMap底层源码解析上 HashMap底层源码解析下 视频链接 小刘老师讲源码 传智播客-黑马程序员 文章目录 树结…
阅读更多...
红黑树原理及java实现

红黑树原理及java实现

红黑树 红黑树规则特点&#xff1a; 节点分为红色或者黑色&#xff1b;根节点必为黑色&#xff1b;叶子节点都为黑色&#xff0c;且为null&#xff1b;连接红色节点的两个子节点都为黑色&#xff08;红黑树不会出现相邻的红色节点&#xff09;&#xff1b;从任意节点出发&…
阅读更多...
红黑树原理及旋转

红黑树原理及旋转

红黑树&#xff0c;本质上来说就是一棵二叉查找树 但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡 保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n) 但它是如何保证一棵n个结点的红黑树的高度始终保持在h logn的呢&#xff1f;这就引出了红黑…
阅读更多...
HashMap红黑树原理分析

HashMap红黑树原理分析

近期学习了 HashMap 实现原理&#xff0c;这篇咱们了解一下红黑树的设计&#xff0c;相比 jdk1.7 的 HashMap 而言&#xff0c;jdk1.8最重要的就是引入了红黑树的设计&#xff0c;当hash表的单一链表长度超过 8 个的时候&#xff0c;链表结构就会转为红黑树结构。 01、故事的起…
阅读更多...
HashMap源码学习：红黑树原理详解

HashMap源码学习：红黑树原理详解

文章导航 HashMap源码学习&#xff1a;红黑树原理详解 HashMap源码学习&#xff1a;JDK1.8版本源码解析 目录 文章导航前言概述红黑树的特性变色平衡右旋平衡左旋平衡 正文红黑树平衡方法&#xff1a;balanceInsertion红黑树左旋方法&#xff1a;rotateLeft红黑树右旋方法&…
阅读更多...
红黑树原理讲解

红黑树原理讲解

红黑树原理讲解 一、红黑树的性质二、红黑树的3种变化策略&#xff1f;&#xff08;为满足红黑树性质&#xff09;1. 改变颜色2. 左旋3. 右旋 三、红黑树的插入情景1&#xff1a;红黑树为空树情景2&#xff1a;插入节点的key已经存在情景3&#xff1a;插入节点的父节点为黑色情…
阅读更多...
红黑树原理详解

红黑树原理详解

红黑树原理详解 红黑树的旋转红黑树上结点的插入红黑树上结点的删除 参考&#xff1a; 教你初步了解红黑树 红黑树(一)之 原理和算法详细介绍 红黑树定义&#xff1a; (1) 每个节点或者是黑色&#xff0c;或者是红色。 (2) 根节点是黑色。 (3) 每个叶子节点是黑色。 [注意&…
阅读更多...
红黑树原理

红黑树原理

因为看的时候写在了纸上&#xff0c;于是直接扫描的&#xff0c;效果不太好。
阅读更多...
HashMap红黑树原理解析

HashMap红黑树原理解析

HashMap红黑树原理解析 定义&#xff1a; 简单来说红黑树是一种近视平衡二叉查找树&#xff0c;主要优点是”平衡”&#xff0c;即左右子树高度几乎一致&#xff0c;以此来防止树退化为链表&#xff0c;通过这种方式来保障查找的时间复杂度为log(n)。 下面先主要提一下红黑树…
阅读更多...
红黑树的原理及实现

红黑树的原理及实现

红黑树的原理及实现 一、什么是红黑树二、定义红黑树三、左旋和右旋四、红黑树插入节点 一、什么是红黑树 红黑树是一种特定类型的二叉树&#xff0c;它是在计算机科学中用来组织数据比如数字的块的一种结构。 红黑树是一种平衡二叉查找树的变体&#xff0c;它的左右子树高差有…
阅读更多...
【图文详解】彻底了解红黑树底层实现原理

【图文详解】彻底了解红黑树底层实现原理

红黑树定义 红黑树&#xff08;Red Black Tree&#xff09; 是一种自平衡二叉查找树&#xff0c;是在计算机科学中用到的一种数据结构&#xff0c;典型的用途是实现关联数组。 红黑树是一种特化的AVL树&#xff08;平衡二叉树&#xff09;&#xff0c;都是在进行插入和删除操…
阅读更多...
红黑树(一)之 原理和算法详细介绍

红黑树(一)之 原理和算法详细介绍

概要 目录1 红黑树的介绍2 红黑树的应用3 红黑树的时间复杂度和相关证明4 红黑树的基本操作(一) 左旋和右旋5 红黑树的基本操作(二) 添加6 红黑树的基本操作(三) 删除 作者&#xff1a;Sky Wang 于 2013-08-08 概述&#xff1a;R-B Tree&#xff…
阅读更多...
数据结构 | 【红黑树】图解原理

数据结构 | 【红黑树】图解原理

今天我们要说的红黑树就是就是一棵非严格均衡的二叉树&#xff0c;均衡二叉树又是在二叉搜索树的基础上增加了自动维持平衡的性质&#xff0c;插入、搜索、删除的效率都比较高。红黑树也是实现 TreeMap 存储结构的基石。 红黑树就是非严格均衡的二叉搜索树。 一、红黑树规则特…
阅读更多...
推荐文章

Copyright @ 2022~2023