HashMap红黑树原理解析

article/2025/11/3 15:42:28

HashMap红黑树原理解析

定义：
简单来说红黑树是一种近视平衡二叉查找树，主要优点是”平衡”，即左右子树高度几乎一致，以此来防止树退化为链表，通过这种方式来保障查找的时间复杂度为log(n)。

下面先主要提一下红黑树的特性:
节点是红色或黑色。
根是黑色。
所有叶子都是黑色（叶子是NIL节点）。
每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

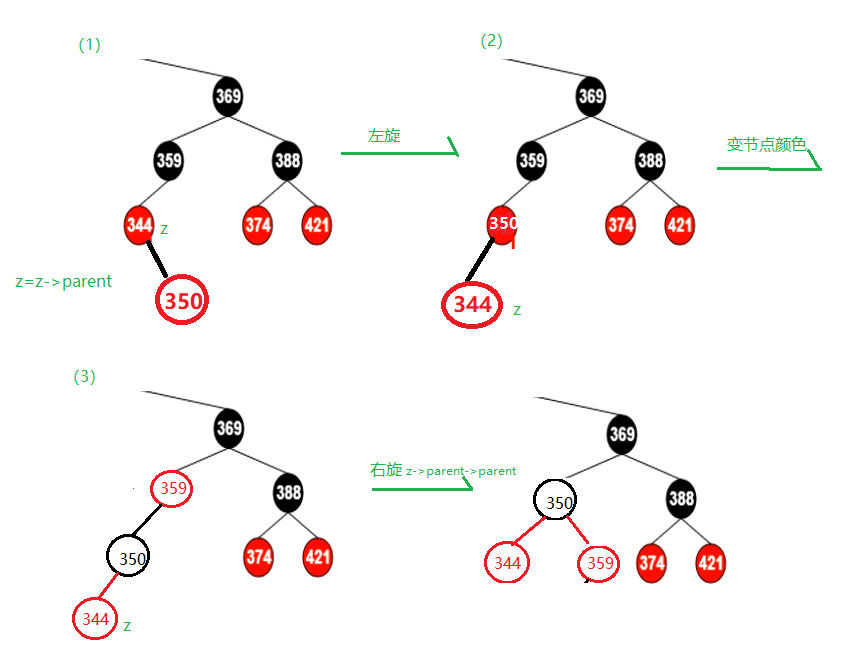
结构如图所示：

在这里插入图片描述
结构调整：
》当红黑树结构发生变化时，红黑树的条件可能会被破坏，需要通过自身调整方能使平衡二叉查找树变为红黑树
调整一般分为两类：
一类是改变某节点颜色(相对简单)
二类是改变树结构(通过左旋、右旋)

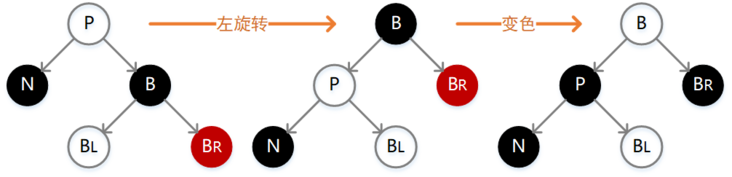
2.1左旋：
如下图所示：
在这里插入图片描述
重点：主要是将P的右子树通过逆时针旋转的方式旋转，成为P节点的父节点，同时将相关节点的引用进行调整，在不改变树的稳定性的前提下，可以使左子树的深度+1，右子树的深度-1，通过这种方式来保证树的平衡

源码分析：
》属性

static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
// 指向父节点指针TreeNode<K,V> parent;  // red-black tree links
// 左孩子指针TreeNode<K,V> left;
// 右孩子指针TreeNode<K,V> right;
// 前驱指针TreeNode<K,V> prev;    // needed to unlink next upon deletion
// 是否为红色节点boolean red;TreeNode(int hash, K key, V val, Node<K,V> next) {super(hash, key, val, next);}

》左旋

static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,TreeNode<K,V> p) {
// r: p的right节点，pp: p的parent节点，rl: p右孩子的左孩子节点 TreeNode<K,V> r, pp, rl;if (p != null && (r = p.right) != null) {// 若R为空,旋转则毫无意义if ((rl = p.right = r.left) != null)//  rl与p右节点=r的左节点(r的左节点不为空)rl.parent = p; // p的左节点则为r.leftif ((pp = r.parent = p.parent) == null)// 若p的父节点为空(root = r).red = false; .// root节点为r并设置黑色else if (pp.left == p)// 判断P节点是根节点的左孩子还是有孩子pp.left = r;elsepp.right = r;r.left = p;p.parent = r;}return root;
}

在这里插入图片描述
2.2右旋
基本逻辑是一样的，只是方向变了，p的左子树绕p顺时针旋转，成为p的parent节点，右子树深度+1，左子树深度-1
如下图所示:

》右旋(与左旋操作一样，只需要将左旋对应的方向换下)

static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,TreeNode<K,V> p) {TreeNode<K,V> l, pp, lr;if (p != null && (l = p.left) != null) {if ((lr = p.left = l.right) != null)lr.parent = p;if ((pp = l.parent = p.parent) == null)(root = l).red = false;else if (pp.right == p)pp.right = l;elsepp.left = l;l.right = p;p.parent = l;}return root;
}

右旋图:
在这里插入图片描述
2.3插入节点

// 插入根据hash值来判断大小
// 如果当前需要插入的类型和正在比对的节点key值是comparable,可以直接通过接口比较
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) {Class<?> kc = null;boolean searched = false;TreeNode<K,V> root = (parent != null) ? root() : this; // 获取根节点for (TreeNode<K,V> p = root;;) {int dir, ph; K pk;  dir:遍历的方向 -1:左孩子方向 1:右孩子方向 ph:p节点hash值if ((ph = p.hash) > h)dir = -1;else if (ph < h)dir = 1;// 因查找二叉树不允许存在相同的key，如果key存在的话则需要返回节点// 则表示插入失败(插入失败，hashmap在后续调用方那会更新值)else if ((pk = p.key) == k || (k != null && k.equals(pk)))return p;else if ((kc == null &&
// 尝试从对象k中找到一个Comparable<x.getClass()> 对象(kc = comparableClassFor(k)) == null) ||(dir = compareComparables(kc, k, pk)) == 0) {if (!searched) {TreeNode<K,V> q, ch;searched = true;
// 如果在p的左子树或者右子树找到目标元素if (((ch = p.left) != null &&(q = ch.find(h, k, kc)) != null) ||((ch = p.right) != null &&(q = ch.find(h, k, kc)) != null))return q;}
// 通过比较两个对象是否是同一类型,如果是,则调用本地方法将两个对象生成对一个的hashcode，hashcode相等的话，则返回-1，否则1dir = tieBreakOrder(k, pk);}TreeNode<K,V> xp = p;
//下面条件成立，则说明找到了目标操作元素if ((p = (dir <= 0) ? p.left : p.right) == null) {Node<K,V> xpn = xp.next;TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);// 元素节点if (dir <= 0)xp.left = x;elsexp.right = x;
//因为TreeNode今后可能退化成链表，因此需要在这里维护链表的next属性xp.next = x;x.parent = x.prev = xp;//节点插入完成if (xpn != null)((TreeNode<K,V>)xpn).prev = x;
//插入操作完成之后就要进行一定的调整操作了moveRootToFront(tab, balanceInsertion(root, x));return null;}}
}

// 获取跟节点
final TreeNode<K,V> root() {for (TreeNode<K,V> r = this, p;;) {// 若父节点为空，则说明当前节点为跟节点if ((p = r.parent) == null)return r;r = p;}
}

2.4查找节点

// 指定key查找对应的TreeNode
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {TreeNode<K,V> p = this;do {int ph, dir; K pk;// 与前面插入节点参数一样TreeNode<K,V> pl = p.left, pr = p.right, q;if ((ph = p.hash) > h)// p的hash元素hashp = pl; // 取p的左子节点else if (ph < h) // 同理相反p = pr; else if ((pk = p.key) == k || (k != null && k.equals(pk)))// 如果key相等return p; // 返回当前元素else if (pl == null)p = pr; else if (pr == null)p = pl;// 如果可以根据compareTo比较则进行比较else if ((kc != null ||(kc = comparableClassFor(k)) != null) &&(dir = compareComparables(kc, k, pk)) != 0)p = (dir < 0) ? pl : pr;// 根据compareTo的结果在右孩子上继续查找else if ((q = pr.find(h, k, kc)) != null)return q;// 若compareTo结果在左孩子上，则继续查找elsep = pl;} while (p != null);return null;
}

2.5确保给定的跟节点是容器的第一个节点

static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {int n;
// 根节点不能为空，table数组不能为空if (root != null && tab != null && (n = tab.length) > 0) {// 获取根节点下标位置int index = (n - 1) & root.hash;TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
// 如果当前下标位置对象与需要验证的对象不是同一个对象if (root != first) {Node<K,V> rn;// 设置红黑树根节点的值设置为头节点tab[index] = root;TreeNode<K,V> rp = root.prev;if ((rn = root.next) != null)
// 将跟节点的下一个节点的上节点指跟节点的上一节点((TreeNode<K,V>)rn).prev = rp;if (rp != null)rp.next = rn; // 将跟节点的上节点的下节点指向跟节点的下一个节点if (first != null)first.prev = root;// 将源头节点上节点指向跟节点root.next = first;// 将跟节点的下节点指向源头节点root.prev = null;// 将跟节点上节点设为null}assert checkInvariants(root);// 检查节点是否满足红黑树规则}
}

参考文章：https://blog.csdn.net/javageektech/article/details/102385013、https://www.jianshu.com/p/34b6878ae6de