文章导航

HashMap源码学习：红黑树原理详解
HashMap源码学习：JDK1.8版本源码解析

前言

JDK1.8后的HashMap引入了红黑树，在学习HashMap源码之前，了解了红黑树原理，及其如何通过代码进行实现后，在整体的看HashMap的源码就会简单很多。

概述

红黑树的特性

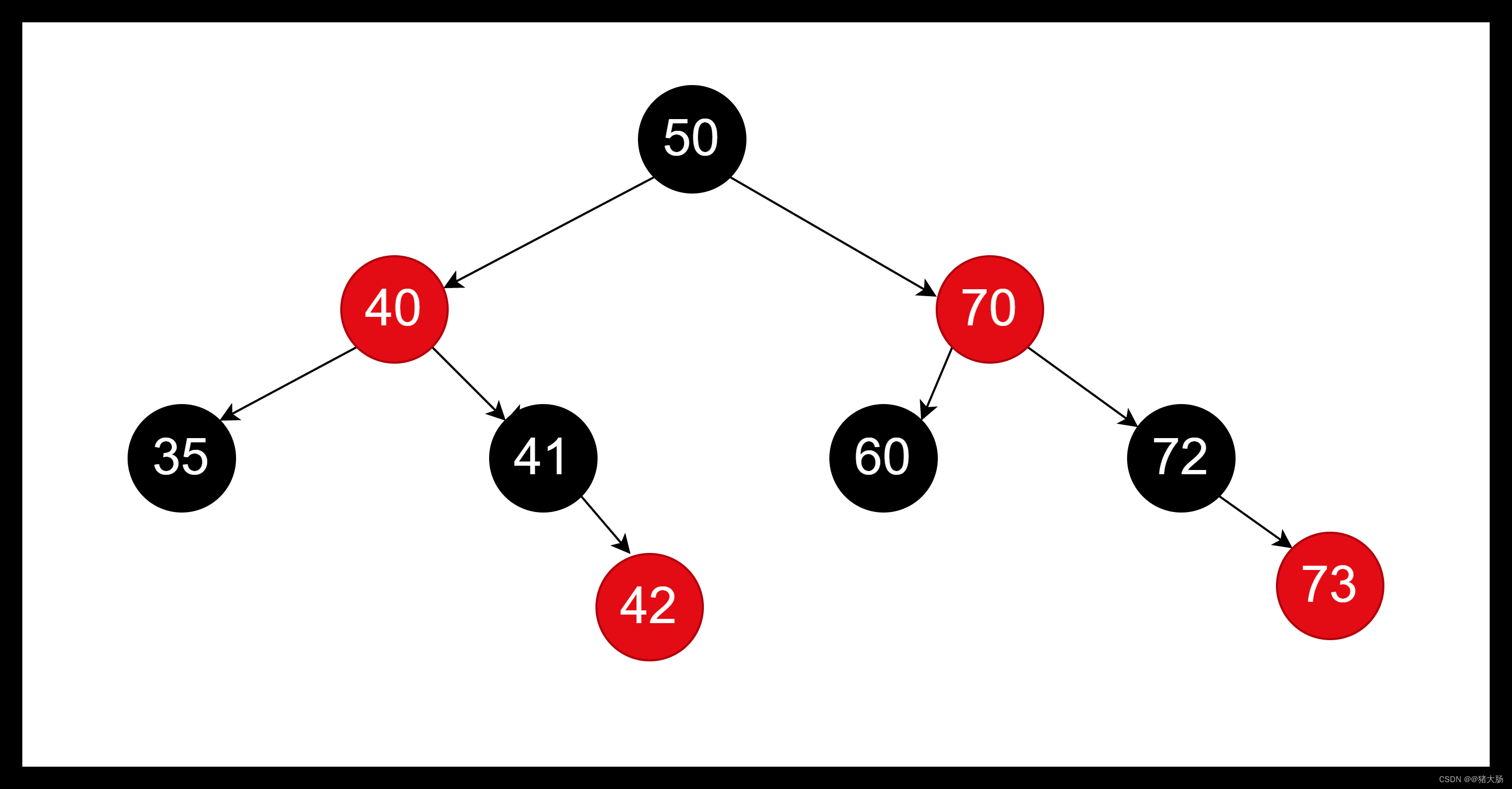
• 根节点必须是黑色节点。
• 节点是红色或黑色。
• 所有叶子都是黑色。（叶子是Null节点）
• 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色节点）
• 从任一结点到其每个叶子的所有路径都包含相同数目的黑色节点。

展示叶子节点

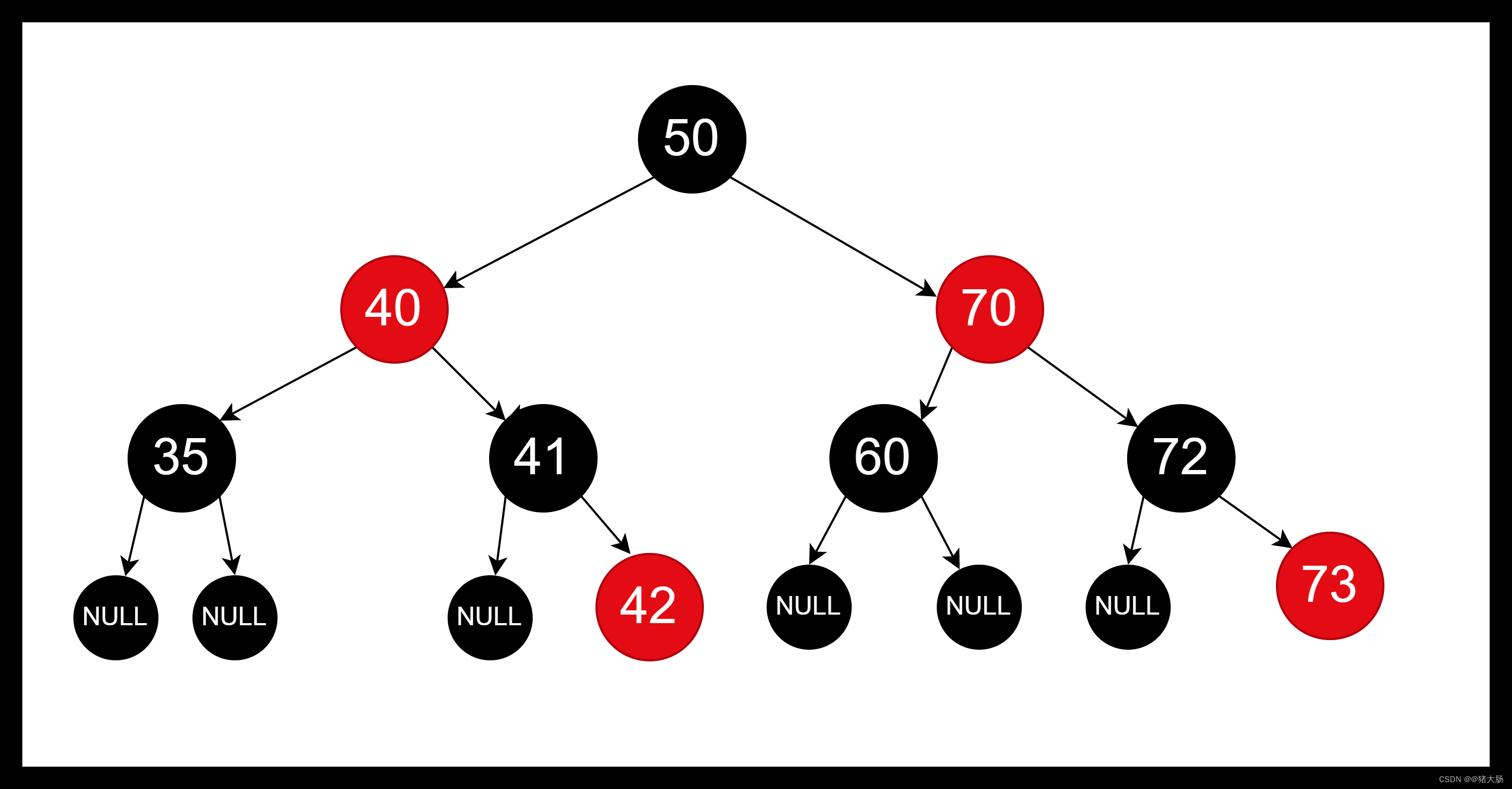
在HashMap源码中红黑树也是需要满足以上条件的，当我们在插入时可能会不满足以上特性，这时候就需要进行位置的调整了，如变色、左旋、右旋等操作来保持红黑树的特性。HashMap中红黑树每次插入节点都是红色节点，如果是插入节点是黑色的，则不满足特性。
如：不满足特性5，不同路径的黑色节点数量不一致。

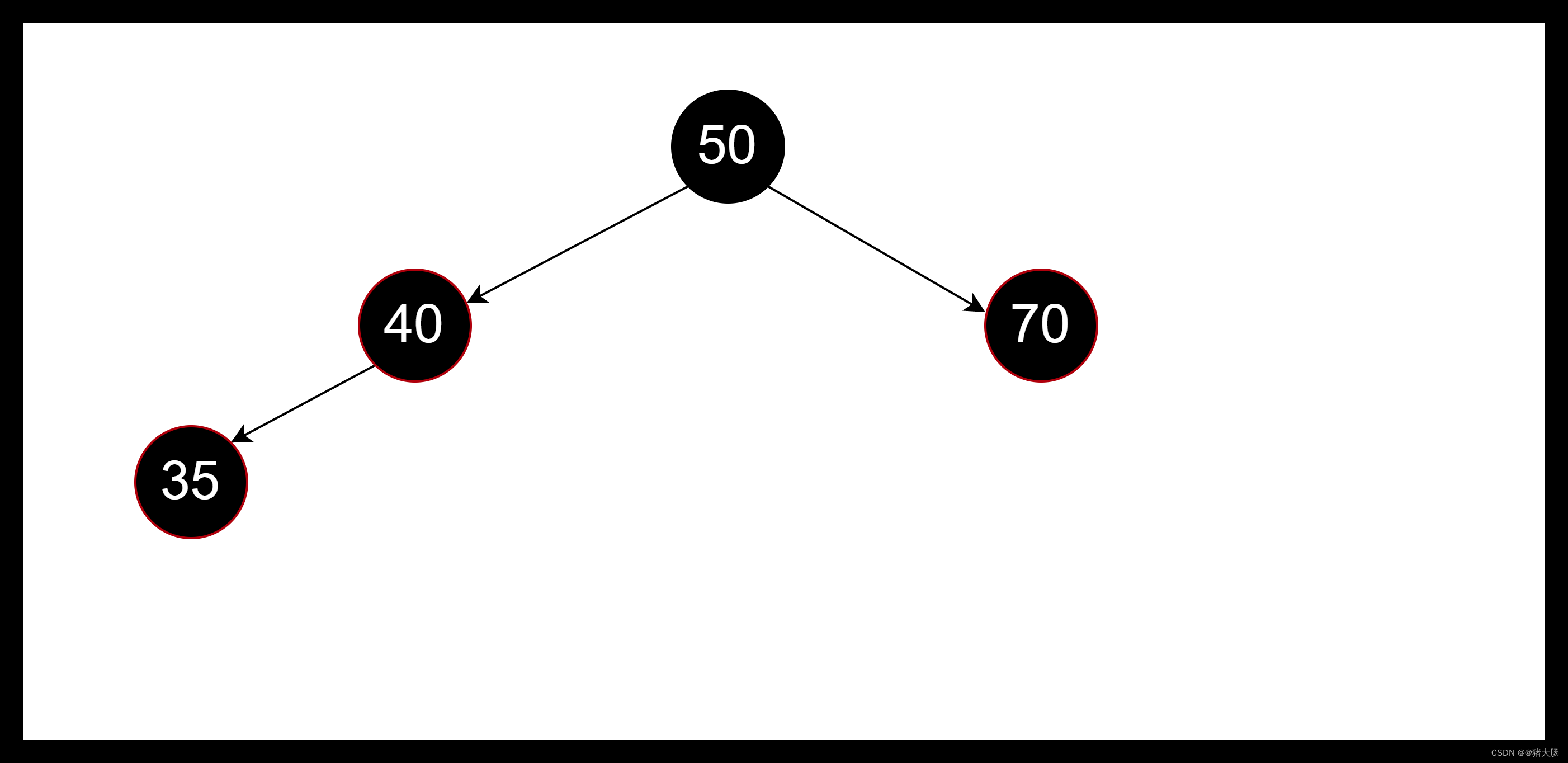
变色平衡

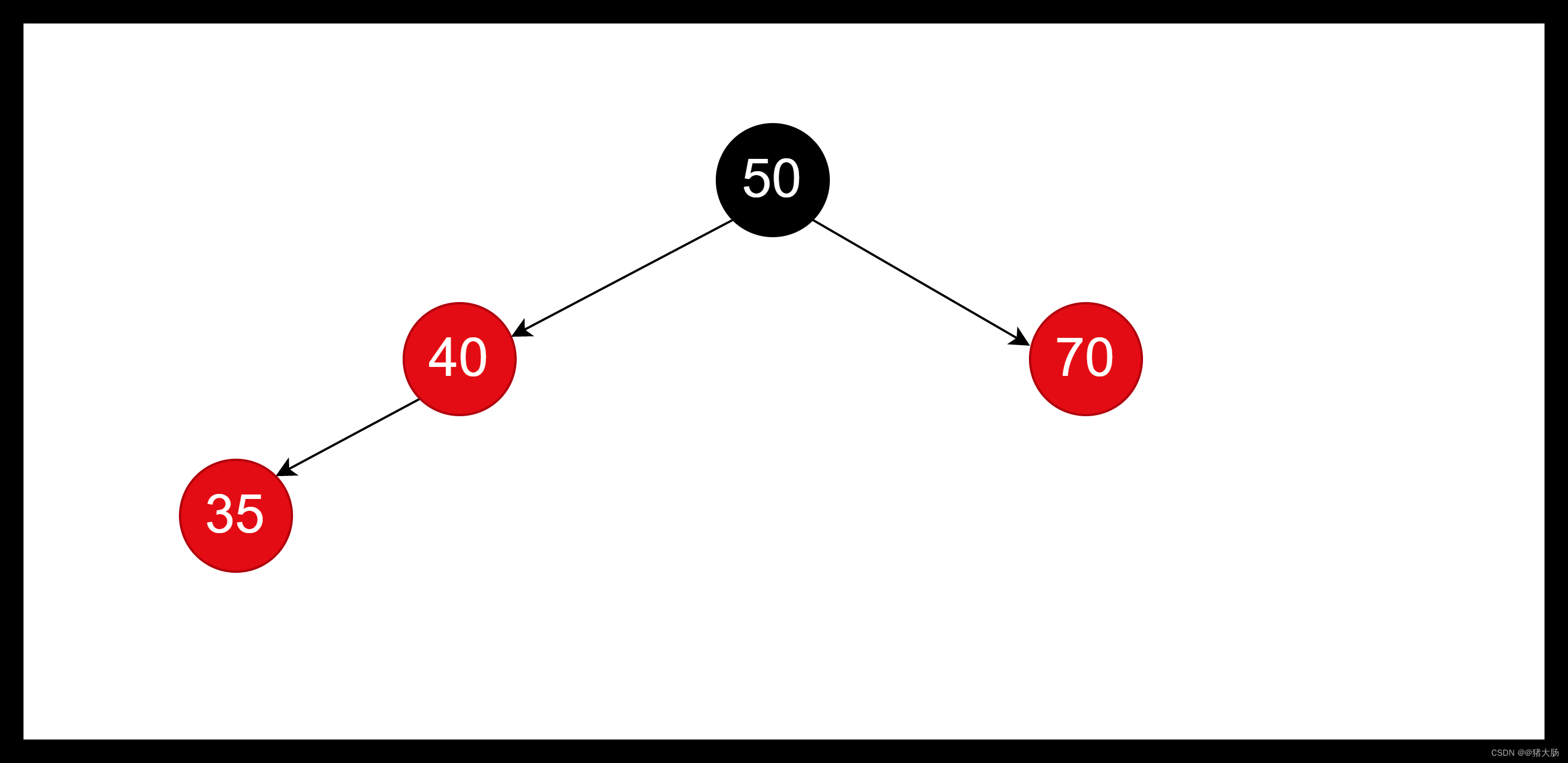
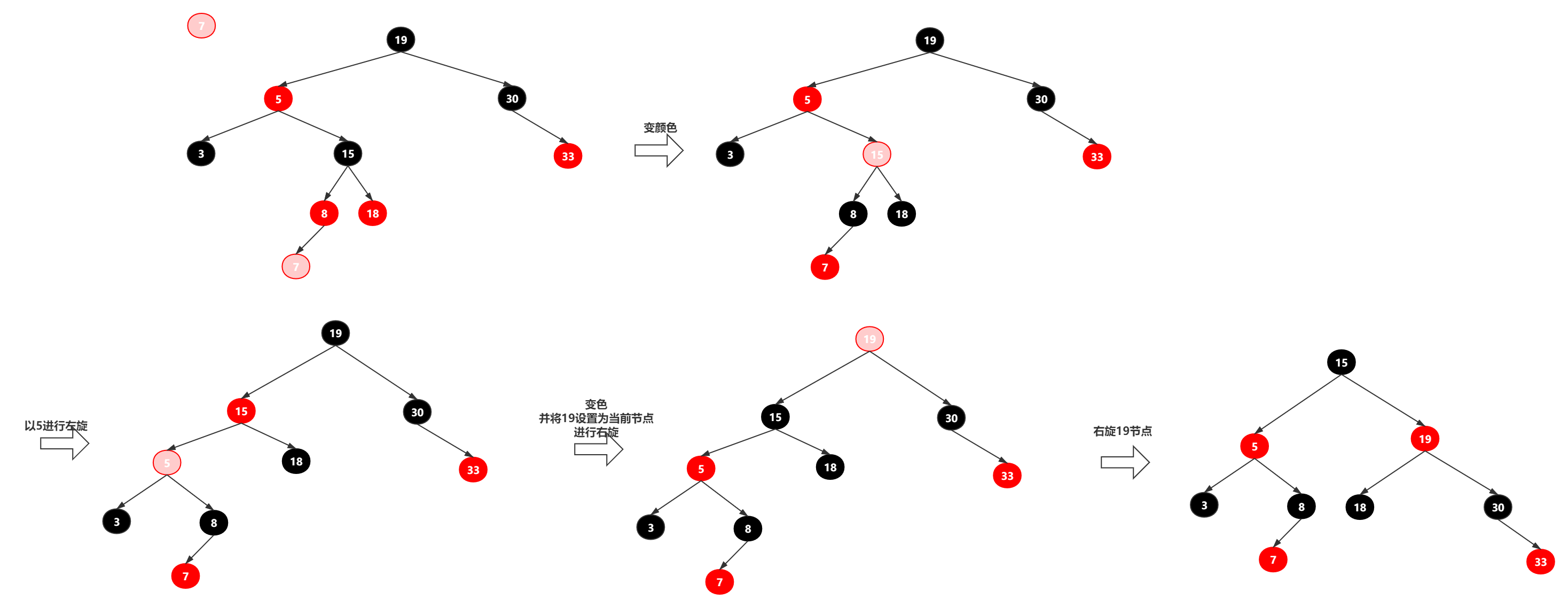
以上结构不符合红黑树特性，插入节点为红色，且父亲节点也为红色，这时需要调整树形结构。我们可以知道在插入红色节点35之前，红黑树肯定是平衡的（不平衡则会进行平衡调节），由于插入节点的父亲是红色，可以判断其爷爷节点50肯定是黑色的，这时候我们判断叔叔节点70是红色的，如果父亲节点跟叔叔节点都是红色的，此时对父亲节点和叔叔节点进行变色调整，由黑色调整为红色，爷爷节点需要从黑色变为空色，但由于爷爷节点是根节点，必须为黑色，所以在变红色后，需要判断是否根节点，如果是根节点则变为黑色，此时红黑S树就平衡了。如果爷爷节点不是根节点，此时就还是红色，有可能爷爷的父亲节点存在红色的情况，所以我们需要将爷爷节点作为插入节点，重复进行平衡操作，直接平衡。

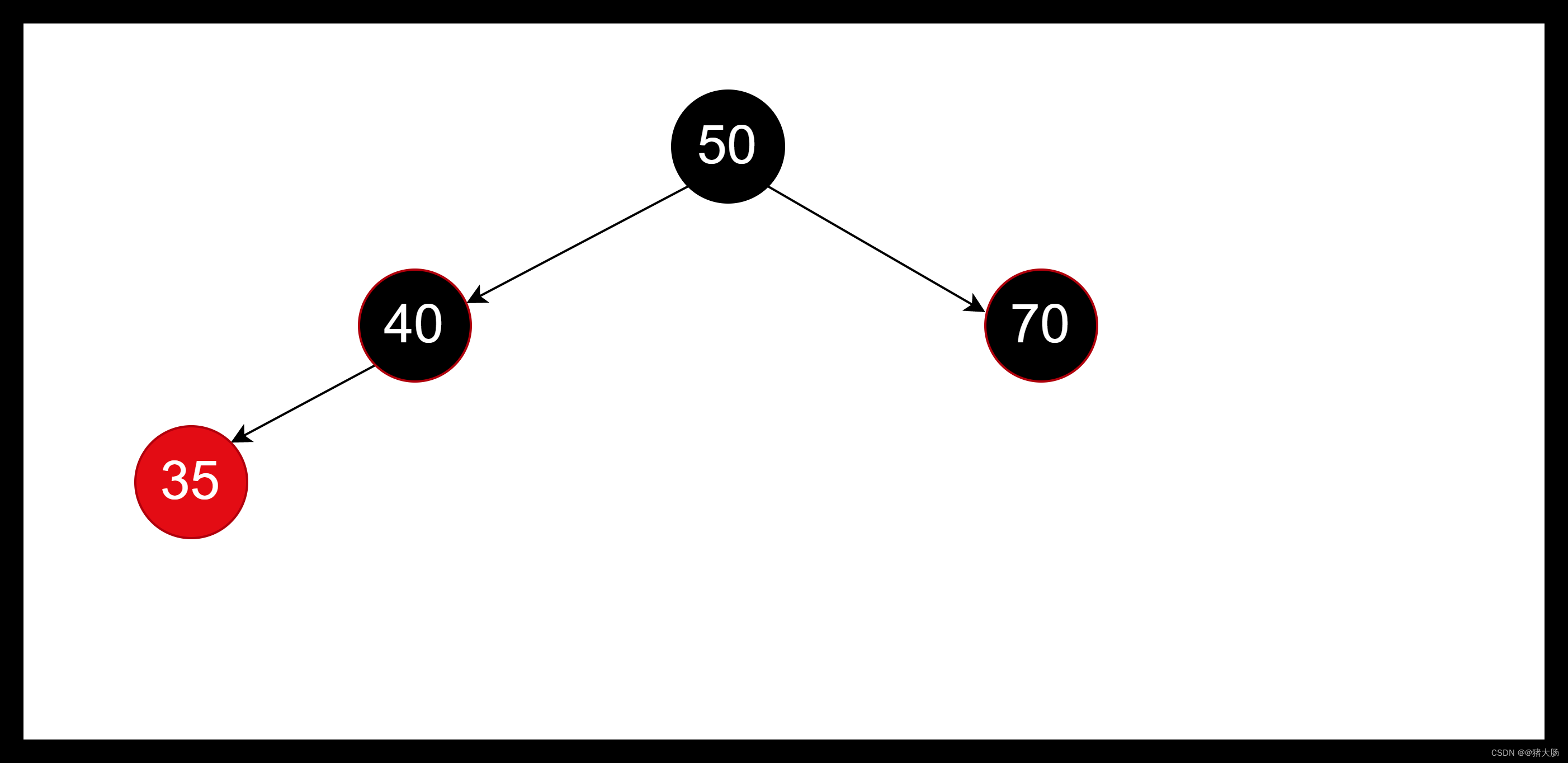
右旋平衡

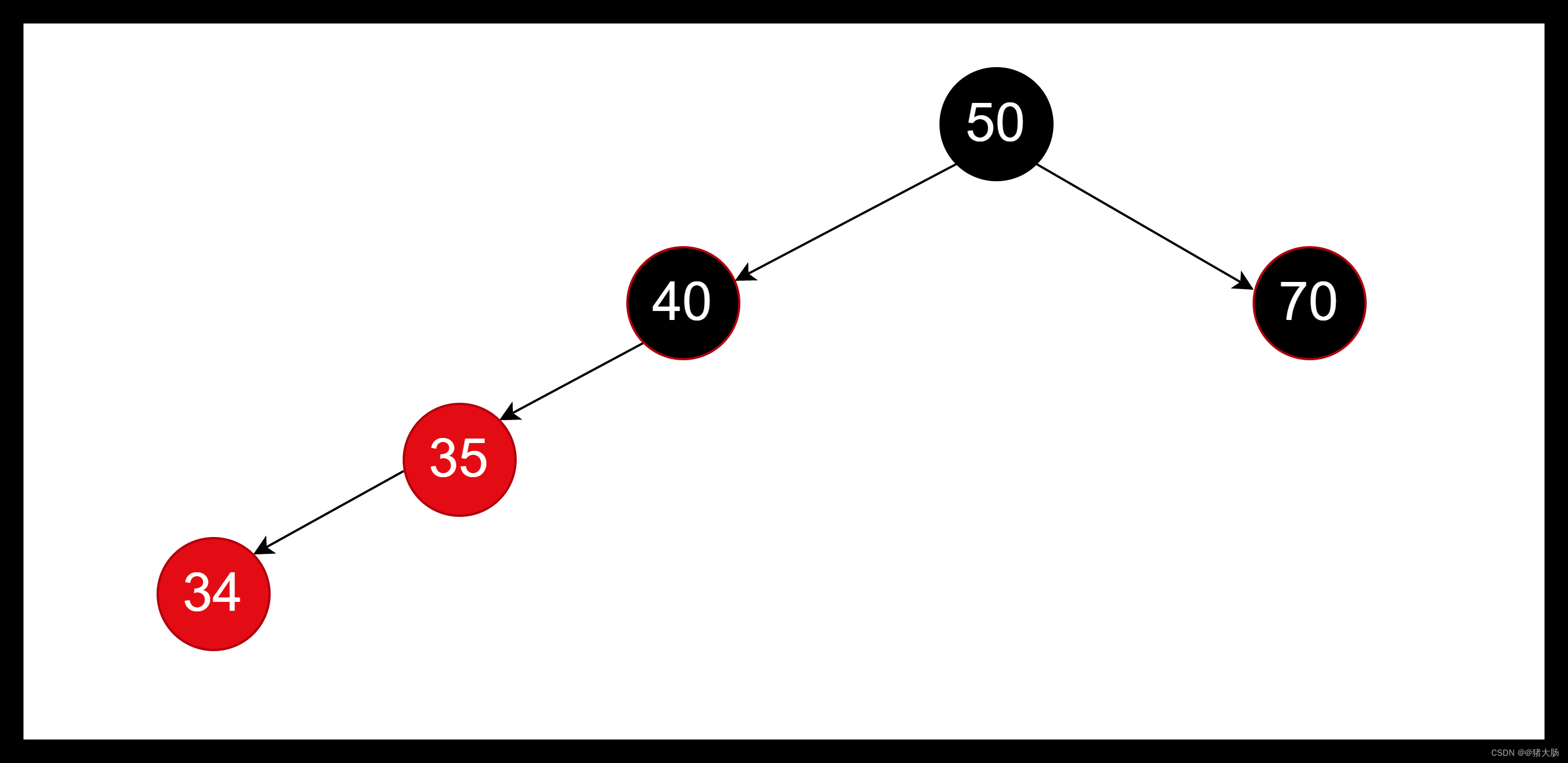
插入红色节点34时，由于其父亲也是红色，不满足红黑树特性。这时候由于其叔叔节点为空，非红色节点，所以不能直接通过变色解决平衡问题。由于插入节点34在父节点35的左边，父亲节点35在爷爷节点40左右，这时候我们可以以爷爷节点40作为旋转点进行右旋。

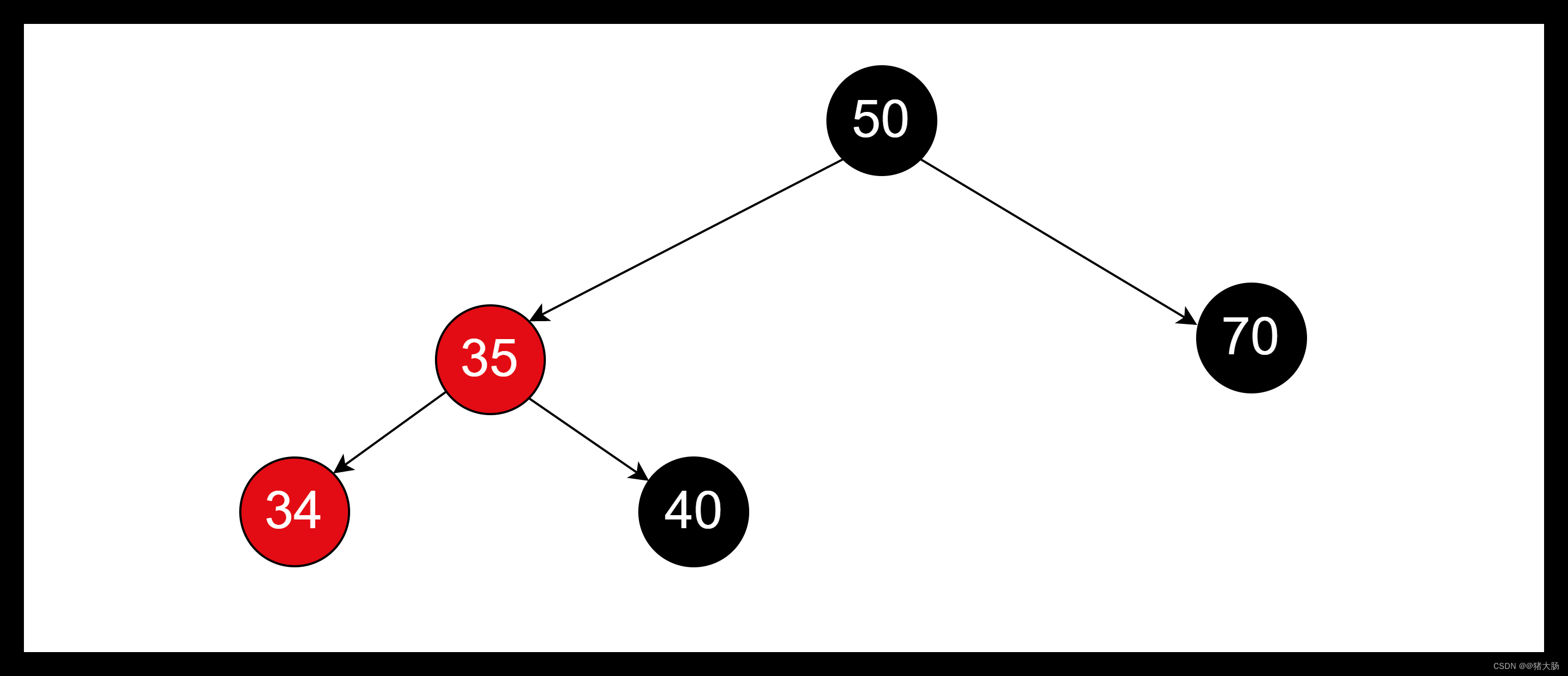
1. 将父节点35的父亲设置为太爷爷节点50
2. 判断爷爷节点40是太爷爷节点50的左边还是右边，如果是左边，则将太爷爷50的左边设置为父亲节点35，右边则设置右边为父亲节点35。
3. 将父亲节点35的右边设置为爷爷节点
4. 将爷爷节点40的父亲设置为父亲夜店35
5. 将爷爷节点40的左边设置为父亲节点35的右边，图中由于父亲节点35的右边是一个NULL节点，所以爷爷节点40的左边也是一个NULL节点。

通过以上步骤，我们发现树形结构还是不平衡，根节点到每个叶子节点黑色数量不是一致的。所以我们还需要调整父亲节点35的颜色为黑色，爷爷节点40颜色为红色，这样达到平衡效果。

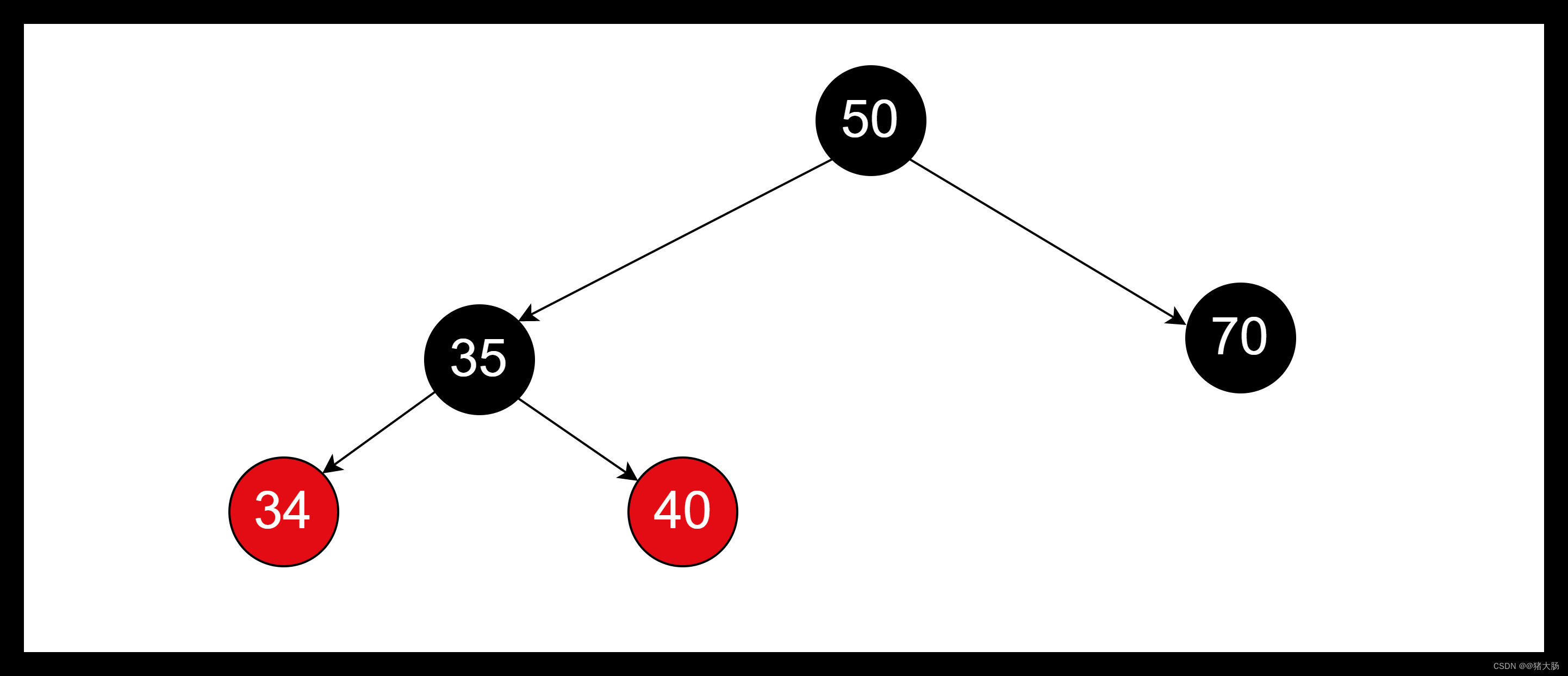
左旋平衡

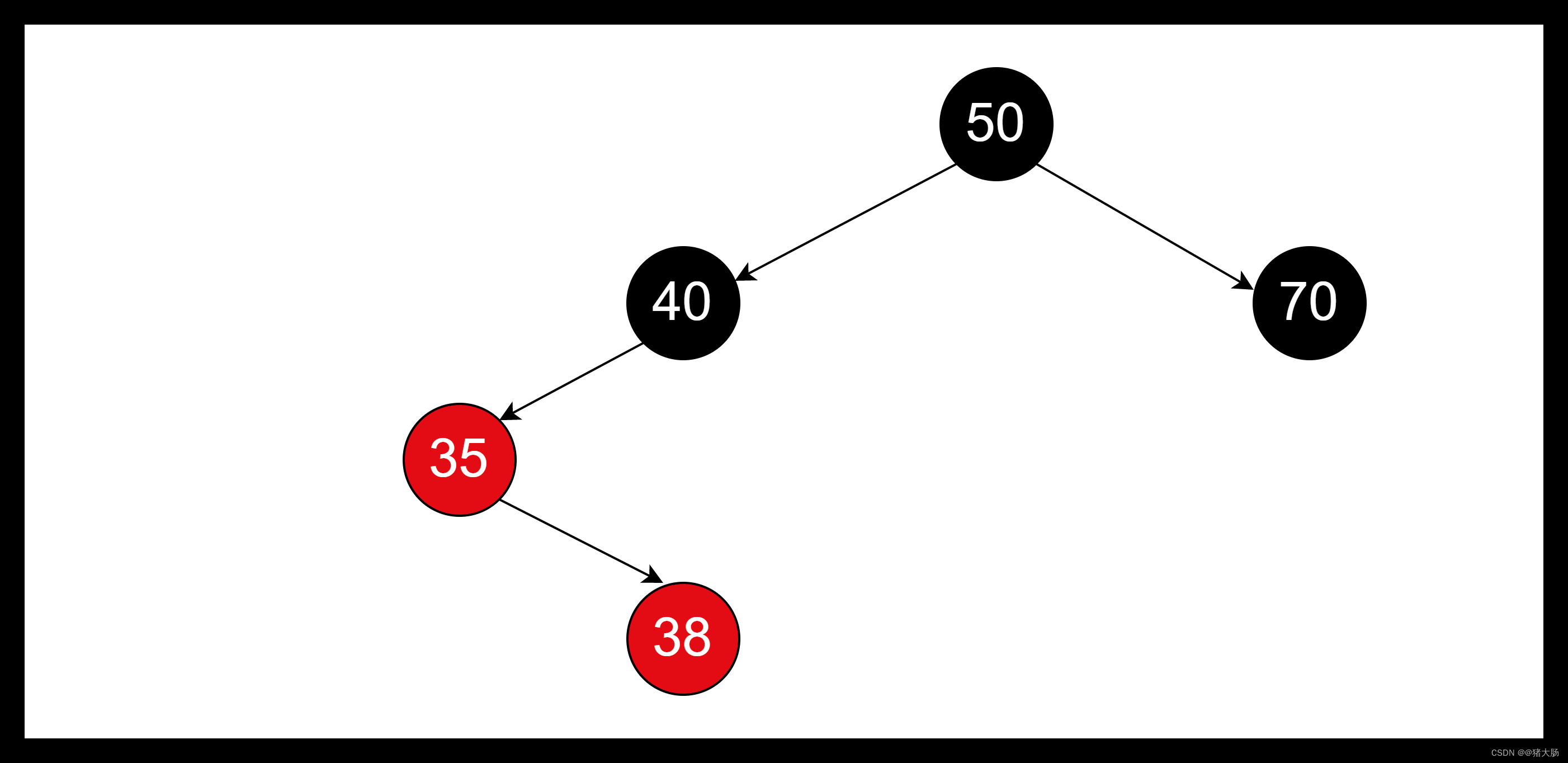
上图中存在两个连续红色的子父节点，不满足红黑色特性，需要通过平衡处理。

1. 判断其叔叔节点是否存在且为红色，如果不满足条件，则无法直接通过变色解决平衡问题。
2. 判断子节点34在父节点35的左边还是右边，如果在右边，则以父亲节点35作为旋转节点进行左旋。

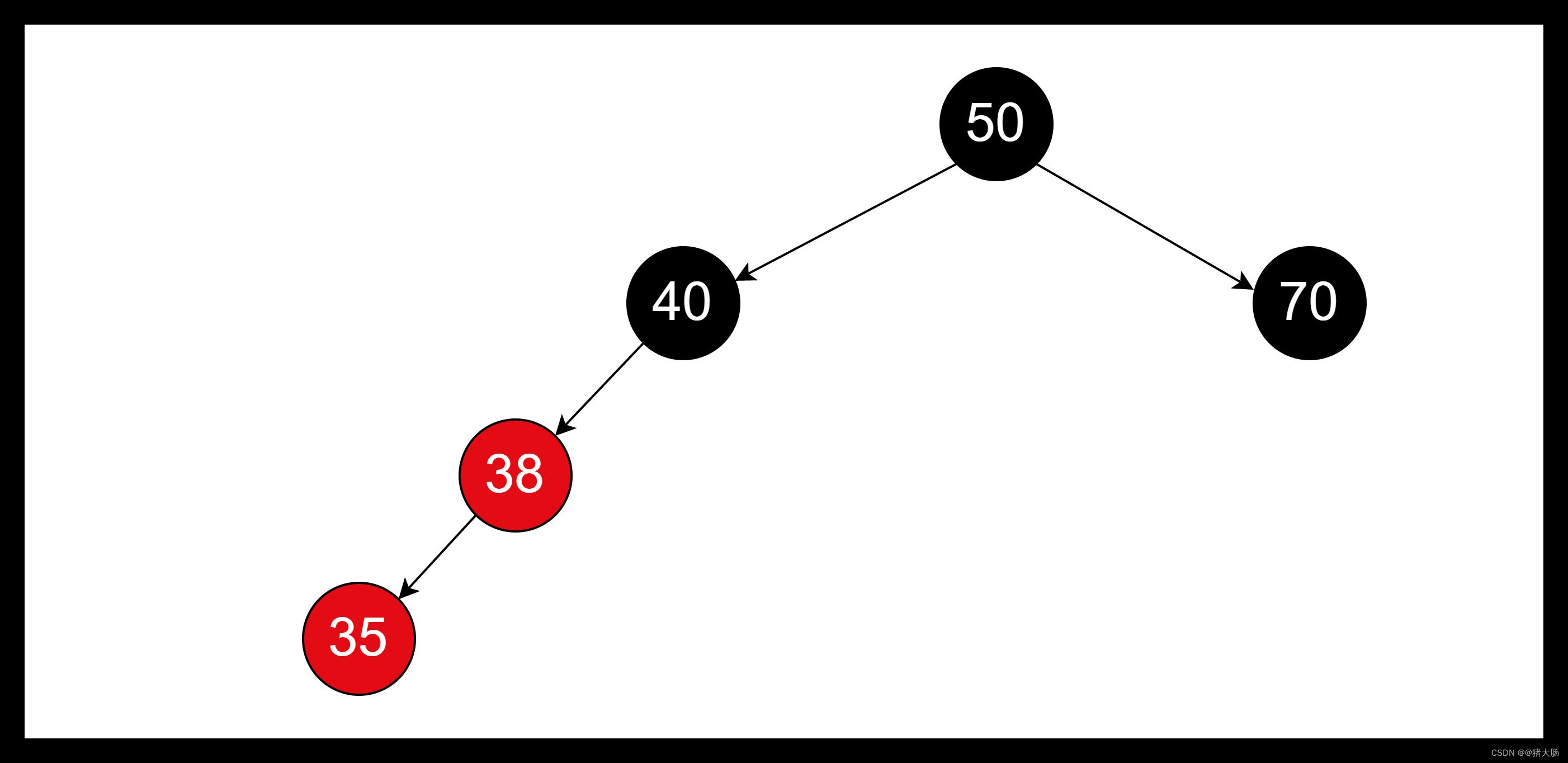
1. 将插入节点38的父亲指向爷爷节点40。
2. 将父亲节点35的父亲指向插入节点38。
3. 将父亲节点35的右边指向插入节点38的左边节点，这里由于插入节点的左边节点为NULL，所以父亲节点35的右边节点也会为NULL。
4. 判断父亲节点35位于爷爷节点的左边还是右边，并将对应的指向插入节点38。

由以上步骤，可以发现此时的树形结构跟我们右旋时所遇到的树形情况一样，这时候再将父亲节点35作为插入节点进行平衡，这里参考本文章的右旋平衡章节。

正文

通过红黑树的特性，我们了解其原理，现在看看HashMap中的平衡是如何进行代码实现的。

红黑树平衡方法：balanceInsertion

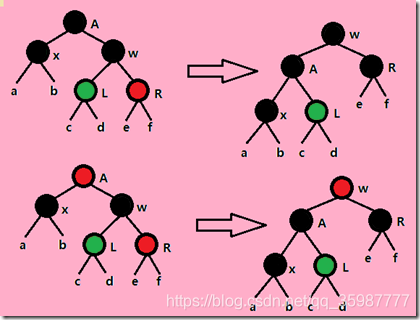
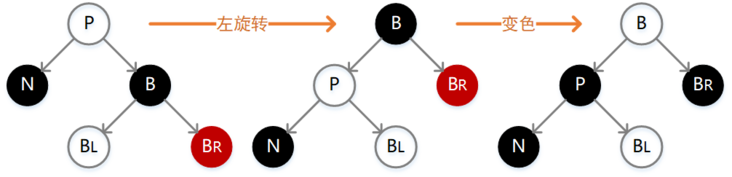
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {x.red = true;//X为插入节点，将其颜色设置为红色//xp为插入节点的父亲//xpp为插入节点的爷爷//xppl、xxpl为其叔叔节点for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {//如果插入节点的父亲为null，证明是其跟节点，此时设置为黑色即可if ((xp = x.parent) == null) {x.red = false;return x;}//如果父亲节点为黑色或者爷爷节点为空，此时证明，父亲节点为根节点。根节点又是黑色，所以插入一个红色节点不会破坏平衡else if (!xp.red || (xpp = xp.parent) == null)return root;if (xp == (xppl = xpp.left)) {//如果父亲节点是爷爷节点的左边时//获取位于右边的叔叔节点，如果叔叔节点不为空且是红色节点。if ((xppr = xpp.right) != null && xppr.red) {//此时进行变色，将父亲跟叔叔节点变为黑色，爷爷节点变为黑色xppr.red = false;xp.red = false;xpp.red = true;//将爷爷节点设置为插入节点，因为爷爷节点变成了红色，可能会破坏平衡，所以需要重新走一边平衡流程x = xpp;}else {//进入这边条件，则证明其右边的叔叔节点为空//判断插入节点是否是父节点的右边if (x == xp.right) {//这种情况跟本文“左旋平衡”中图示情况一致//以父亲作为旋转节点进行左旋，左旋之后此时的树还不是平衡状态，此时还是存在两个连续的红色节点root = rotateLeft(root, x = xp);//重新定义父亲节点，并给爷爷节点赋值xpp = (xp = x.parent) == null ? null : xp.parent;}if (xp != null) {//将父亲节点设置为黑色xp.red = false;if (xpp != null) {//将爷爷节点设置为红色，并进行右旋，此时红黑树就平衡了。xpp.red = true;root = rotateRight(root, xpp);}}}}else {//进入这里，证明父亲节点是爷爷节点的右边。这里的操作跟上面条件里面是操作是反过来的。//判断是否存在红色的叔叔节点if (xppl != null && xppl.red) {//将父亲节点、叔叔节点设置为黑色，将爷爷节点设置为红色，此时有可能会破坏平衡，需要将爷爷节点作为插入节点，继续走平衡流程xppl.red = false;xp.red = false;xpp.red = true;x = xpp;}else {//如果插入节点为父亲节点的左边if (x == xp.left) {//先进行右旋root = rotateRight(root, x = xp);//重新定义父亲节点，并给爷爷节点赋值xpp = (xp = x.parent) == null ? null : xp.parent;}if (xp != null) {//将父亲节点设置为黑色xp.red = false;if (xpp != null) {//将爷爷节点设置为红色，以爷爷节点作为旋转节点进行左旋xpp.red = true;root = rotateLeft(root, xpp);}}}}}}

rotateLeft方法，左旋见方法2详解

rotateRight方法，右旋见方法3详解

红黑树左旋方法：rotateLeft

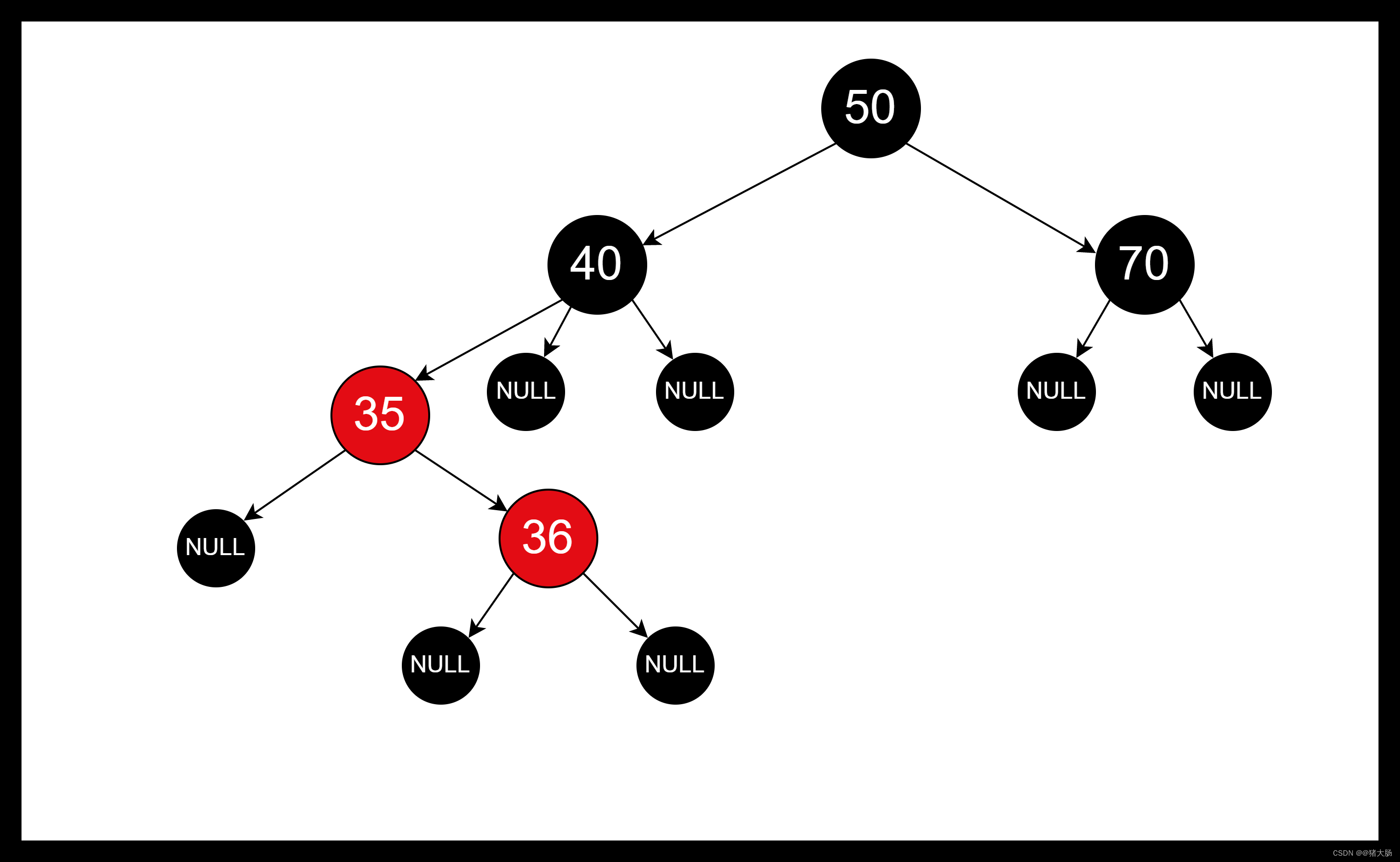
上图中的旋转节点为：节点35

        static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,TreeNode<K,V> p) {TreeNode<K,V> r, pp, rl;//r为旋转节点的右边节点  简称：旋转右节点//pp为旋转节点的父亲节点  简称：旋转父节点//rl旋转右节点的左边节点  简称：旋右左节点//判断旋转节点和旋转右节点不为null，并对旋转右节点进行赋值if (p != null && (r = p.right) != null) {//判断旋右左节点不为空，并将旋转节点的右边设置为旋右的左节点，并对旋右左节点rl进行赋值if ((rl = p.right = r.left) != null)//将旋右左节点的父亲设置为旋转节点rl.parent = p;//旋转右节点的父亲设置为其爷爷节点，并判断其爷爷节点是否为空if ((pp = r.parent = p.parent) == null)//为空则证明所处位置为根节点，将其设置为黑色(root = r).red = false;//判断旋转节点是在其父亲节点左边还是右边else if (pp.left == p)//将旋转节点父亲的左边设置为旋转右节点pp.left = r;else//将旋转节点父亲的右边设置为旋转右节点pp.right = r;//将旋转右节点的左边设置为旋转节点r.left = p;//将旋转节点的父亲设置为旋转右节点p.parent = r;}return root;}

红黑树右旋方法：rotateRight

右旋跟左旋是对应反着来的。

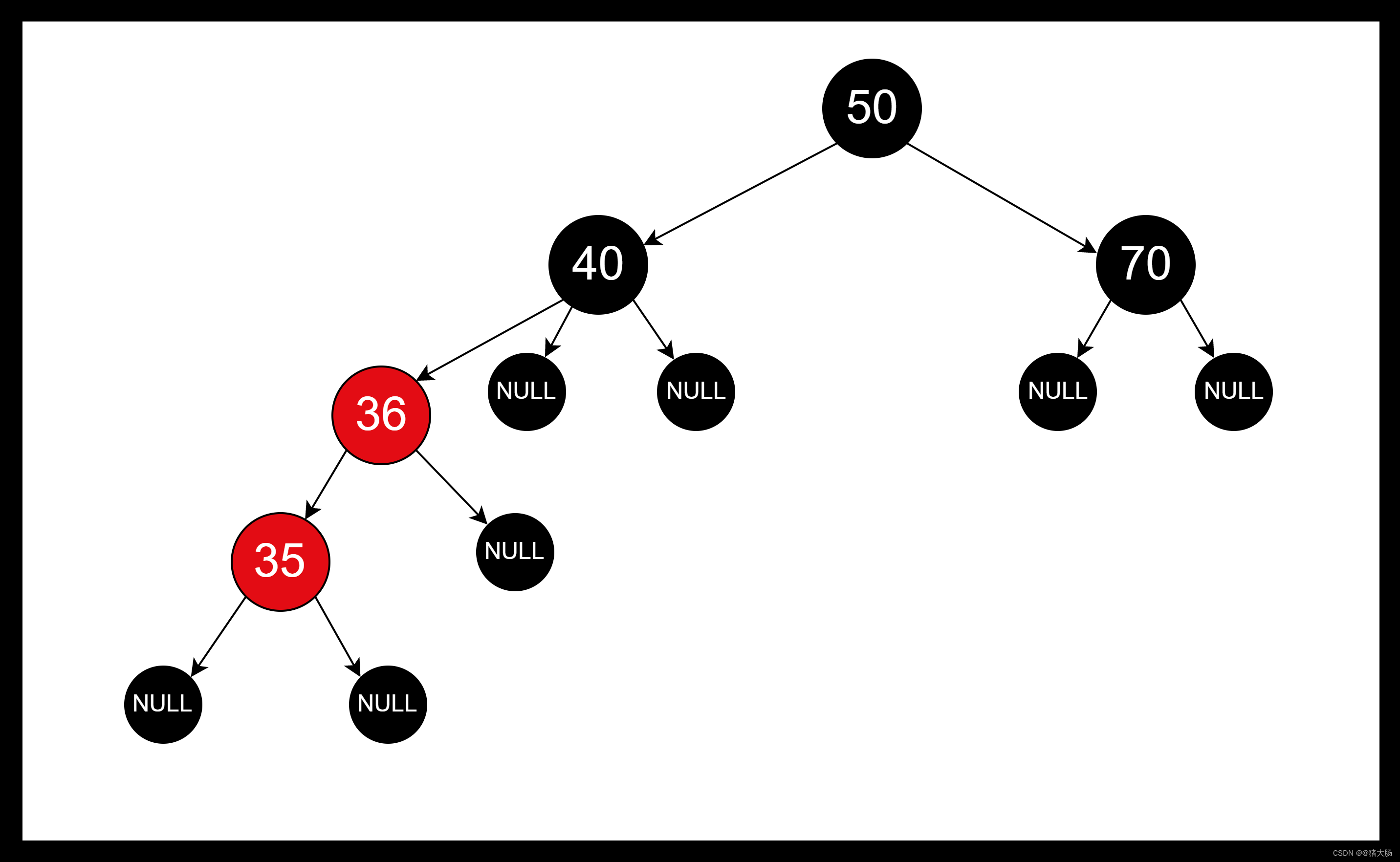
上图中的旋转节点为：节点40

static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,TreeNode<K,V> p) {TreeNode<K,V> l, pp, lr;//l为旋转节点的右边节点  简称：旋转左节点//pp为旋转节点的父亲节点  简称：旋转父节点//lr旋转右节点的右边节点  简称：旋左右节点//判断旋转节点和旋转左节点不为null，并对旋转左节点进行赋值if (p != null && (l = p.left) != null) {//判断旋左左节点不为空，并将旋转节点的左边设置为旋左的右节点，并对旋左右节点lr进行赋值if ((lr = p.left = l.right) != null)//将旋左右节点的父亲设置为旋转节点lr.parent = p;//旋转左节点的父亲设置为其爷爷节点，并判断其爷爷节点是否为空if ((pp = l.parent = p.parent) == null)//为空则证明所处位置为根节点，将其设置为黑色(root = l).red = false;else if (pp.right == p)//将旋转节点父亲的右边设置为旋转左节点pp.right = l;else//将旋转节点父亲的右边设置为旋转右节点pp.left = l;//将旋转左节点的右边设置为旋转节点l.right = p;//将旋转节点的父亲设置为旋转左节点p.parent = l;}return root;}

红黑树添加方法：putTreeVal

上面讲解了红黑树的平衡操作，现在进入红黑树的添加节点方法中。

        final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) {Class<?> kc = null;boolean searched = false;//获取其根节点TreeNode<K,V> root = (parent != null) ? root() : this;for (TreeNode<K,V> p = root;;) {//p:根节点//dir：-1代表左边节点方向 1代表右边节点方向//hash：插入节点的key hash值//key：插入节点的key值//pk：当前所在节点的key值int dir, ph; K pk;//判断插入节点key的hash值与当前节点比较大小，确定走向if ((ph = p.hash) > h)dir = -1;else if (ph < h)dir = 1;//判断当前节点的key是否相等，相等则查到了位置else if ((pk = p.key) == k || (k != null && k.equals(pk)))return p;//有可能存入的key实现了比较器，所以这里会尝试获取比较器来重新计算下一节点树的方向else if ((kc == null &&(kc = comparableClassFor(k)) == null) ||(dir = compareComparables(kc, k, pk)) == 0) {if (!searched) {TreeNode<K,V> q, ch;//标记为已经查找过了searched = true;//尝试从根节点的左节点或右节点进行查询，查询到该节点时，则返回该节点if (((ch = p.left) != null &&(q = ch.find(h, k, kc)) != null) ||((ch = p.right) != null &&(q = ch.find(h, k, kc)) != null))return q;}dir = tieBreakOrder(k, pk);}TreeNode<K,V> xp = p;//判断此时的方向是往哪边查找if ((p = (dir <= 0) ? p.left : p.right) == null) {//获取当前节点的下个节点值Node<K,V> xpn = xp.next;//如果不存在该相同的key信息，则创建新的节点，TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);//判断新插入节点放在左边还是右边if (dir <= 0)xp.left = x;elsexp.right = x;//当前节点的链表下个节点指向插入节点xp.next = x;//将插入节点的红黑树父节点，及其链表的上个节点指向当前节点。x.parent = x.prev = xp;//如果当前节点原先的链表下个节点不为空，则将其链表的上个节点指向新插入的节点。if (xpn != null)((TreeNode<K,V>)xpn).prev = x;//将ROOT节点的位置放到数组的第一个位置中moveRootToFront(tab, balanceInsertion(root, x));return null;}}}

到最后这块的代码涉及了链表的赋值，有读者可能有疑问，明明是红黑树怎么又对链表进行操作了？
HashMap1.8引入了红黑树，当链表节点个人>=8个时，会转为红黑树。当节点个数<=6个时，会转为链表。所以我们在操作红黑树的插入操作时，需要记录节点的上个节点，及其下个节点的指向，以便后续转为链表。

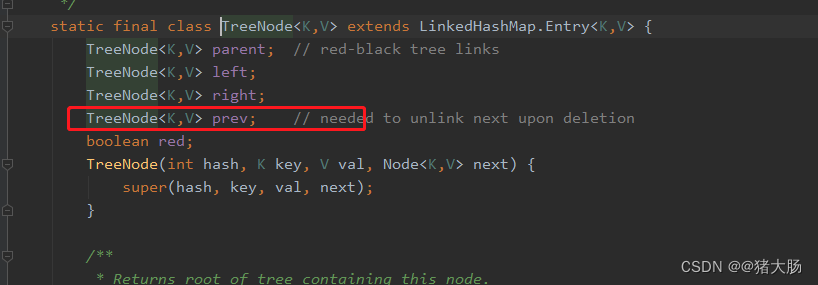
我们可以看到红黑树节点都有prev属性，而TreeNode继承了Node，所以也有了next属性。

红黑树查询方法：find

 final TreeNode<K,V> find(int h, Object k, Class<?> kc) {//将红黑树所在的当前节点赋值给pTreeNode<K,V> p = this;do {int ph, dir; K pk;TreeNode<K,V> pl = p.left, pr = p.right, q;//比较当前节点的hash值大小，决定查找方向if ((ph = p.hash) > h)p = pl;else if (ph < h)p = pr;//能走到这里证明hash值是一样的，如果key值一样，则是查找到了else if ((pk = p.key) == k || (k != null && k.equals(pk)))return p;//能走到这里证明hash值是一样的（hash冲突情况），如果左边节点为null,则赋值为右边，从右边进行查询，否则从左边查询else if (pl == null)p = pr;else if (pr == null)p = pl;//走到这里，证明还没办法确定走向，所以尝试获取key是否实现Comparable，并重新计算出其方向else if ((kc != null ||(kc = comparableClassFor(k)) != null) &&(dir = compareComparables(kc, k, pk)) != 0)p = (dir < 0) ? pl : pr;//递归，从右边节点进行查找，如果查不到则从左边进行查找else if ((q = pr.find(h, k, kc)) != null)return q;elsep = pl;} while (p != null);//找不到返回nullreturn null;}

红黑树删除方法：removeTreeNode

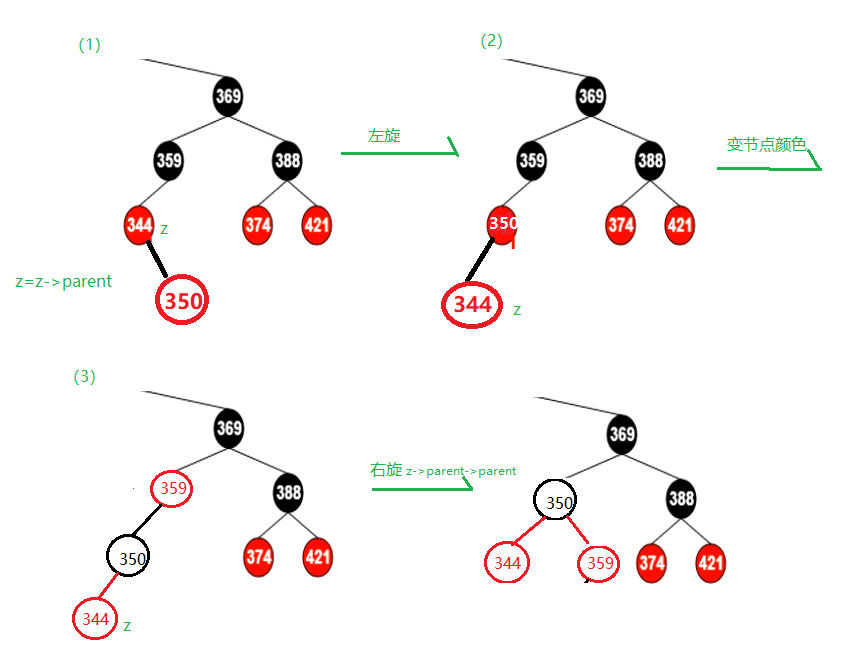
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,boolean movable) {int n;if (tab == null || (n = tab.length) == 0)return;//计算出所在的数组下标int index = (n - 1) & hash;//获取当前下标中的第一个值，也就是跟节点TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;//获取当前移除节点的下个节点，及其上个节点的指向值TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;//移除节点上个节点为空，则证明其排在第一位，需要将数组下标中的第一个节点重新赋值if (pred == null)tab[index] = first = succ;else//将上个节点的next指向移除节点的下个节点pred.next = succ;//下个节点不为空，则将下个节点的prev 指向移除节点的prev节点。if (succ != null)succ.prev = pred;if (first == null)return;//如果第一个节点的父节点有值，则获取当前红黑树的根节点if (root.parent != null)root = root.root();//如果根节点不存在 ，节点树为0//movable默认为true&&根节点的右边为空，节点数小于3//根节点的左节点为空，节点数小于3//左节点的左节点为空时，节点数小于等于6if (root == null|| (movable&& (root.right == null|| (rl = root.left) == null|| rl.left == null))) {//链表化，因为前面对链表节点完成了删除操作，故在这里完成之后直接返回，即可完成节点的删除tab[index] = first.untreeify(map);  // too smallreturn;}//p为删除节点//pl为删除节点的左节点//pr为删除节点的右节点//replacement 为删除节点的替换节点TreeNode<K,V> p = this, pl = left, pr = right, replacement;if (pl != null && pr != null) {//这里的目的是获取删除节点的右边中最小值来替换当前被删除节点，这样才能保证树形特性。也可以查询删除节点的左边中的最大值节点来替换TreeNode<K,V> s = pr, sl;while ((sl = s.left) != null) // find successors = sl;//获取待替换节点的颜色C,将待替换节点颜色与删除节点保持一致，将删除节点颜色替换为待替换节点颜色。这里就是将待替换节点与删除节点进行替换工作boolean c = s.red; s.red = p.red; p.red = c; // swap colors//获取待替换节点的右节点TreeNode<K,V> sr = s.right;//获取删除节点的父节点TreeNode<K,V> pp = p.parent;//如果待替换节点的父节点为删除节点的右边if (s == pr) { // p was s's direct parent//交换两个节点的位置，父节点变子节点，子节点变父节点p.parent = s;s.right = p;}else {//这里整块逻辑就是将删除节点与待替换节点进行互换，但是删除节点的左边节点，其父亲节点还未改变//获取待替换节点的父节点TreeNode<K,V> sp = s.parent;//将删除节点的父节点指向待替换节点的父节点，这里将删除节点的位置替换到待替换节点中if ((p.parent = sp) != null) {if (s == sp.left)sp.left = p;elsesp.right = p;}//将删除节点的右边节点，其父节点替换为待替换节点if ((s.right = pr) != null)pr.parent = s;}//将删除节点的左节点设置为空p.left = null;//将删除节点右边设置为待替换节点的右节点，并将替换节点的右节点，其父亲替换为删除节点if ((p.right = sr) != null)sr.parent = p;//待替换节点的左节点设置为删除节点的左节点，并且将该左节点的父节点设置为待替换节点if ((s.left = pl) != null)pl.parent = s;//待替换节点的父节点设置为删除节点的父节点，如果为空则设置待替换节点为根节点，否则将删除节点的父节点，其对应的左节点或右节点进行替换。if ((s.parent = pp) == null)root = s;else if (p == pp.left)pp.left = s;elsepp.right = s;//设置待移除的节点，这里主要判断删除节点替换位置后，是否是最后一个节点，如果是则后面将其删除，不是则移除节点设置为其右边的节点，后面再把移除的右边节点赋值给替换后的删除节点，达到删除的效果if (sr != null)replacement = sr;elsereplacement = p;}//走到这里证明删除节点的右边为Null,此时其左边节点作为替换节点，否则为将其右边节点作为替换节点else if (pl != null)replacement = pl;else if (pr != null)replacement = pr;else//到这里，证明删除节点没有子节点，所以替换节点设置为本身replacement = p;//由于替换节点是根删除节点相邻，所以将替换节点顶替其删除节点，这样删除节点就从树中被移除了，再将其属性都置为nullif (replacement != p) {TreeNode<K,V> pp = replacement.parent = p.parent;if (pp == null)root = replacement;else if (p == pp.left)pp.left = replacement;elsepp.right = replacement;p.left = p.right = p.parent = null;}//如果删除节点是红色的，替换者肯定是黑色的，所以不需要进行平衡操作，否则需要进行平衡TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);//到这里证明删除节点处于最后一个节点时if (replacement == p) {  // detach//将删除节点从树中移除TreeNode<K,V> pp = p.parent;p.parent = null;if (pp != null) {if (p == pp.left)pp.left = null;else if (p == pp.right)pp.right = null;}}//保持根节点处于 所在数组index位置中的第一个节点if (movable)moveRootToFront(tab, r);}

总结

为了保持红黑树的特性，在插入或者删除时，可能破坏其平衡结构，所以通过变色、左旋、右旋等方式来保持红黑树的平衡。

红黑树特性：

• 根节点必须是黑色节点。
• 结点是红色或黑色。
• 所有叶子都是黑色。（叶子是Null节点）
• 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色节点）
• 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。