红黑树定义
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
红黑树是一种特化的AVL树(平衡二叉树),都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目。(来源百度百科)
结构特点

特性
是一种 自平衡 的二叉树,所谓的自平衡是指在插入和删除的过程中,红黑树会采取一定的策略对树的组织形式进行调整,以尽可能的减少树的高度,从而节省查找的时间。
红黑树的特性如下:
结点是红色或黑色
根结点始终是黑色
叶子结点(NIL 结点)都是黑色
红色结点的两个直接孩子结点都是黑色(即从叶子到根的所有路径上不存在两个连续的红色结点)
从任一结点到每个叶子的所有简单路径都包含相同数目的黑色结点
以上性质保证了红黑树在满足平衡二叉树特征的前提下,还可以做到 从根到叶子的最长路径最多不会超过最短路径的两倍 ,这主要是考虑两个极端的情况,由性质 4 和 5 我们可以知道在一棵红黑树上从根到叶子的最短路径全部由黑色结点构成,而最长结点则由红黑结点交错构成(始终按照一红一黑的顺序组织),又因为最短路径和最长路径的黑色结点数目是一致的,所以最长路径上的结点数是最短路径的两倍。
自平衡策略
对于一棵红黑树的操作最基本的无外乎增删改查,其中查和改都不会改变树的结构,所以与普通平衡二叉树操作无异。剩下的就是增删操作,插入和删除都会破坏树的结构,不过借助一定的平衡策略能够让树重新满足定义。平衡策略可以简单概括为三种: 左旋转 、 右旋转 ,以及 变色 。在插入或删除结点之后,只要我们沿着结点到根的路径上执行这三种操作,就可以最终让树重新满足定义。
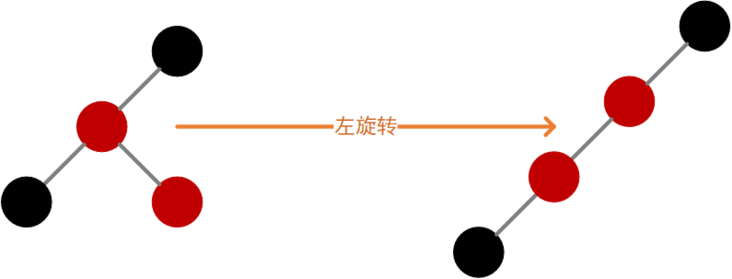
- 左旋转
对于当前结点而言,如果右子结点为红色,左子结点为黑色,则执行左旋转,如下图:
- 右旋转
对于当前结点而言,如果左子、左孙子结点均为红色,则执行右旋转,如下图:

- 变色
对于当前结点而言,如果左、右子结点均为红色,则执行变色,如下图:

插入操作
红黑树作为平衡二叉树的一种,同样需要借助于查找操作定位插入点,不过红黑树约定新插入的结点一律为红色,这主要也是为了简化树的自平衡过程。对于一棵空树而言,插入结点为红色会增加一次变色操作,但是对于其余的情况,如果插入的结点是一个黑色结点,那么必然会破坏性质 5,而插入一个红色结点有可能会破坏性质 4,但是此时我们可以通过简单的策略对树进行调整以重新满足定义。
约定 X 为插入的结点,P 为 X 的父结点,G 为 X 的祖父结点,U 为 X 的叔叔结点。
- 1.新插入结点 X 是根结点
此时新插入结点为红色,违背性质 2,只需将其变为黑色即可
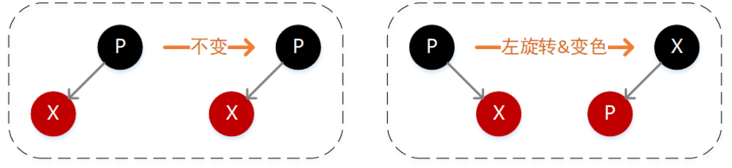
- 2.新插入结点 X 的父结点 P 是黑色
此时需要依据新插入结点 X 值相对于父结点 P 的大小分为两种情况,如果小于则将 X 简单插入到 P 的左子位置即可(下图左),如果 X 的值大于 P,则需要将 X 插入到 P 的右子结点位置,然后执行一次左旋转即可(下图右)。
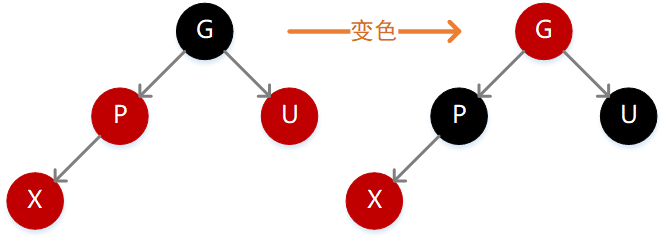
- 3.父结点 P 为红色,同时存在叔叔结点 U 也为红色
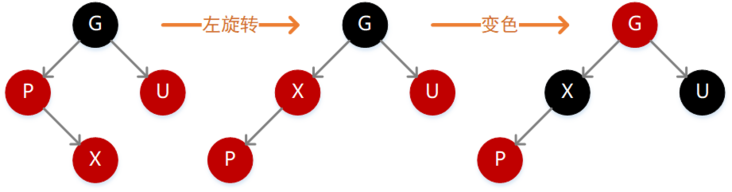
因为 P 为红色,按照性质 4 则 G 必定为黑色,如果 X 的值小于 P,则需要在 P 的左子位置插入(如下图),插入后不满足性质 4,此时只需要执行一次变色操作,将 P、G、U 的颜色反转一下即可,因为 G 变为红色,所以路径长度减 1,但是因为 P 和 U 都变为了黑色,所以路径长度又加 1,最终长度不变,但此时 G 变为了红色,所以需要继续向上递归。
如果 X 的值大于 P,则需要在 P 的右子位置插入(如下图),插入后不满足性质 4,此时需要先执行左旋转变为上面这种情况,继续变色即可。
- 4.父结点 P 为红色,同时叔叔结点 U 为黑色或不存在
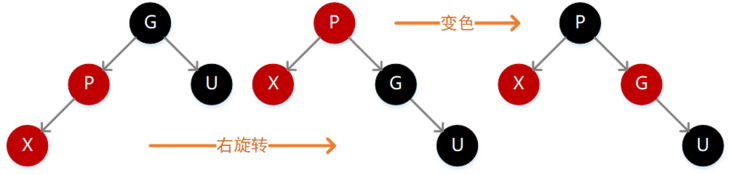
因为 P 为红色,按照性质 4 则 G 必定为黑色,如果 X 的值小于 P,则需要在 P 的左子位置插入(如下图),插入后不满足性质 4,此时需要先执行一次右旋转,旋转之后仍然违背性质 4,同时左子树的高度减 1,这个时候需要再执行一次变色操作即可满足定义。
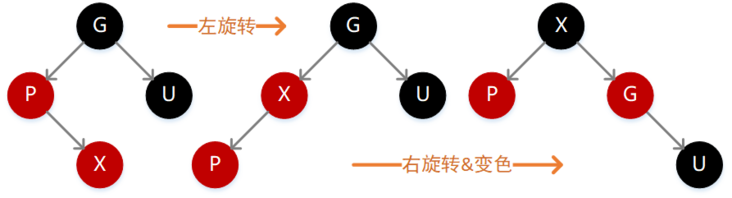
如果 X 的值大于 P,则需要在 P 的右子位置插入(如下图),插入后不满足性质 4,此时我们需要执行一次左旋转,然后就转换成了上面这种情况,继续右旋转、变色即可。
删除操作
红黑树作为平衡二叉树的一种,同样需要借助于查找操作定位删除点,在执行删除之前我们需要判断待删除结点有几个孩子结点,如果是 2 个的话我们需要从结点的左子树中寻找值最大的结点,或者从右子树中寻找值最小的结点,并用结点值替换掉待删除结点(只要目标结点值从树上消失即可,不要纠结具体删除的是哪个结点)。这两个结点有一个共性,即最多只有一个孩子结点(因为已经是自己所处范围内的最大和最小了),此时就将需求转变成删除只有一个孩子结点的结点,相对要简单了许多。
约定 X 为待删除的结点,P 为 X 的父结点,S 为 X 的孩子结点,B 为 X 的兄弟结点,BL 为 B 的左孩子结点,BR 为 B 的右孩子结点。
如果待删除结点 X 是一个红色结点,则直接删除即可,不会违反定义。
如果待删除结点 X 是一个黑色结点,且其孩子结点 S 是红色的,那么只需要将 X 替换成 S,同时将 S 由红变黑即可。
如果需要删除的结点 X 是黑色的,同时它的孩子结点 S 也是黑色的,这种情况需要进一步分场景讨论。
对于第三种情况我们首先将 X 替换成 S,并重命名其为 N,N 沿用 X 对于长辈和晚辈的称呼,需要清楚这里实际删除的是 X 结点,并且删除之后通过 N 的路径长度减 1。
- 1.N 是新的根
这种情况比较简单,不需要再做任何调整。
- 2.N 的父结点、兄弟结点 B,以及 B 的孩子结点均为黑色
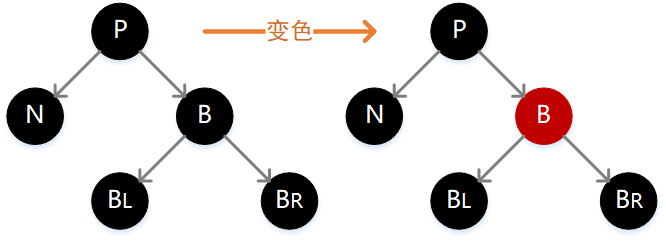
如下图,此时只需要将 B 变为红色即可,这样所有通过 B 的路径减 1,与所有通过 N 的路径正好一致,但是此时通过 P 的路径都减少了 1 个长度,所以需要向上递归对结点 P 继续判定。
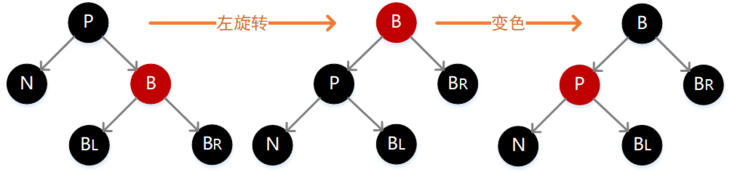
- 3.N 的兄弟结点 B 为红色,其余结点均为黑色
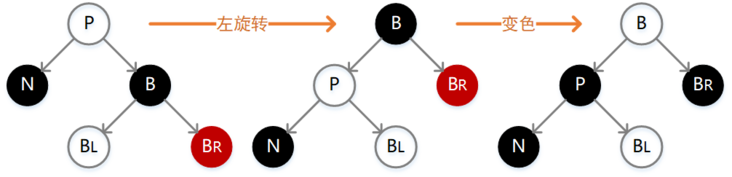
如下图,此时需要执行一次左旋转,然后将 P 和 B 的颜色互换。调整前后各个结点的路径没有变化,但是因为之前经过 N 的路径长度少了一个单位,所以此时仍然不满足定义,需要按照后面的场景继续调整。
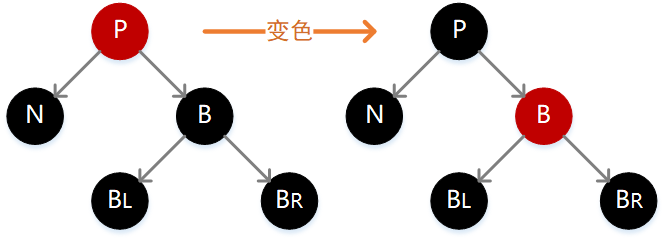
- 4.N 的父结点 P 为红色,兄弟结点 B,以及 B 的孩子结点均为黑色
如下图,此时我们只需要简单互换 P 和 B 的颜色,这种情况下对于不通过 N 的结点路径没有影响,但是却让通过 N 的结点路径加 1,正好弥补之前删除操作所带来的损失。
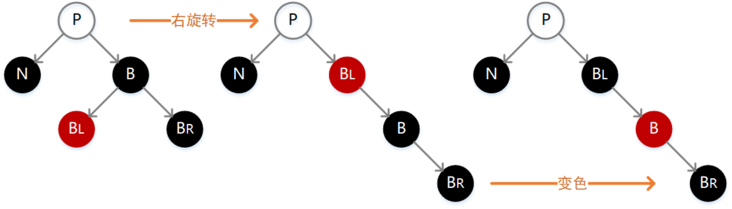
- 5.N 的兄弟结点 B 为黑色,B 的左孩子为红色,B 的右孩子为黑色
如下图,此时我们需要先执行一次右旋转操作,然后互换 B 与 BL 的颜色,操作之后通过所有结点的路径长度并没有发生变化,却让 N 有了一个新的黑色兄弟结点,并且该兄弟结点的右孩子为红色,从而可以按照接下去介绍的一种场景继续调整。
注:白色结点表示该结点既可以是黑色也可以是红色,后续图示亦是如此。
- 6.N 的兄弟结点 B 为黑色,B 的右孩子为红色
如下图,此时我们需要先执行一次左旋转,并互换 P 和 B 的颜色,同时将 B 的右孩子结点变为黑色。变更之后,除 N 外其余结点的路径长度未发生变化,但是经过 N 的路径上却增加了一个黑色结点,这刚好弥补之前删除操作所带来的损失。