介绍红黑树之前可以先了解一下二叉搜索树和AVL树，毕竟红黑树是为了弥补二叉搜索树的不足而诞生的嘛

一、红黑树的性质

• 性质1：每个节点要么是黑色，要么是红色
• 性质2：根节点是黑色
• 性质3：每个叶子节点（NIL）是黑色
• 性质4：每个红色节点的两个子节点一定都是黑色。不能有两个红色节点相连
• 性质5：任意一节点到每个叶子节点的路径都包含数量相同的黑结点。俗称：黑高！
• 性质5.1：如果一个节点存在黑子节点，那么该结点肯定有两个子节点

二、红黑树的3种变化策略？（为满足红黑树性质）

1. 改变颜色

结点的颜色由红变黑或由黑变红

2. 左旋

动图演示

静态图演示

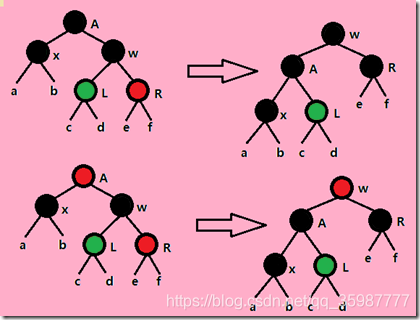
3. 右旋

动态图演示

静态图演示

三、红黑树的插入

注意：

插入节点，必须为红色，理由很简单，红色在父节点（如果存在）为黑色节点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。
但如果插入结点是黑色，那么插入位置所在的子树黑色结点总是多1，必须做自平衡。

在开始每个情景的讲解前，我们还是先来约定下:

情景1：红黑树为空树

最简单的一种情景，直接把插入结点作为根结点就行
注意：根据红黑树性质2：根节点是黑色。还需要把插入结点设为黑色

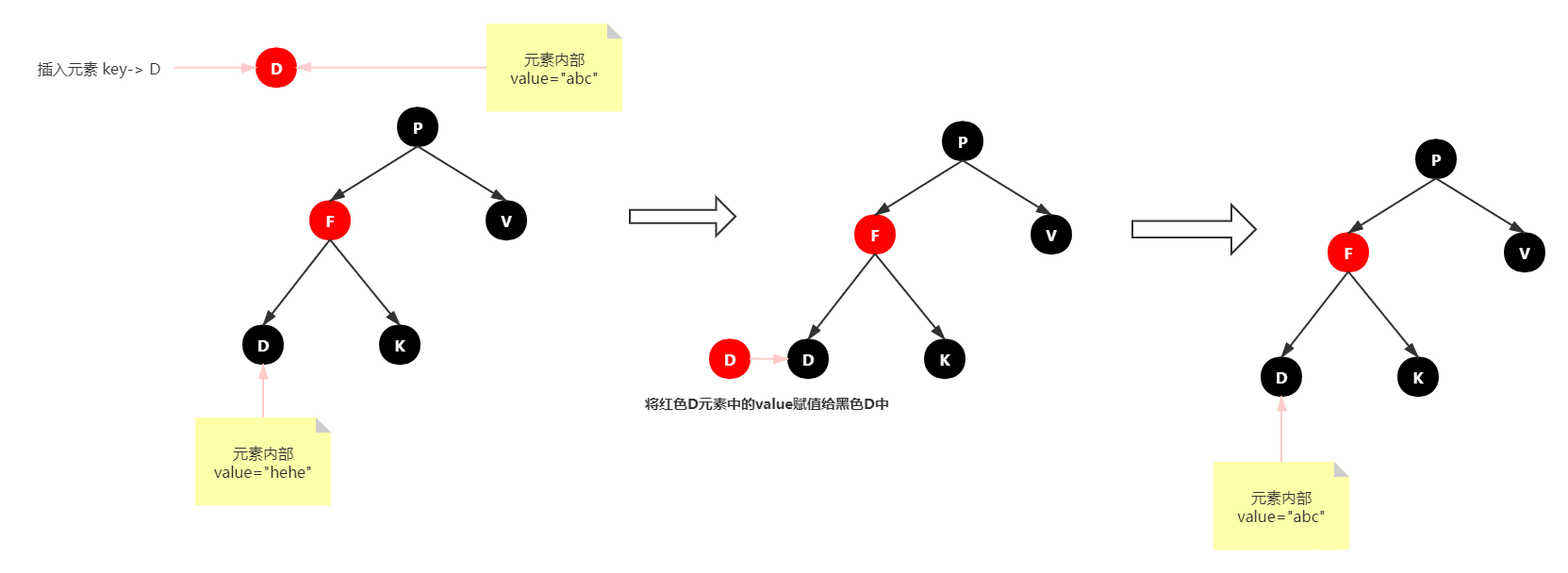
情景2：插入节点的key已经存在

更新当前节点的值，为插入节点的值

情景3：插入节点的父节点为黑色

由于插入的结点是红色的，并不会影响红黑树的平衡，直接插入即可，无需做自平衡

情景4：插入节点的父节点为红色

根据红黑树的性质2：根结点是黑色。如果插入节点的父结点为红结点，那么该父结点不可能为根结点，所以插入结点总是存在祖父结点。后续的旋转操作肯定需要祖父结点的参与

情景4.1：叔叔节点存在，并且为红色（父-叔 双红）

依据红黑树性质4可知，红色节点不能相连 ==> 祖父结点肯定为黑结点；
因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是：黑红红。显然最简单的处理方式是把其改为：红黑红
处理：
1.将P和U节点改为黑色
2.将PP改为红色
3.将PP设置为当前节点，进行后续处理

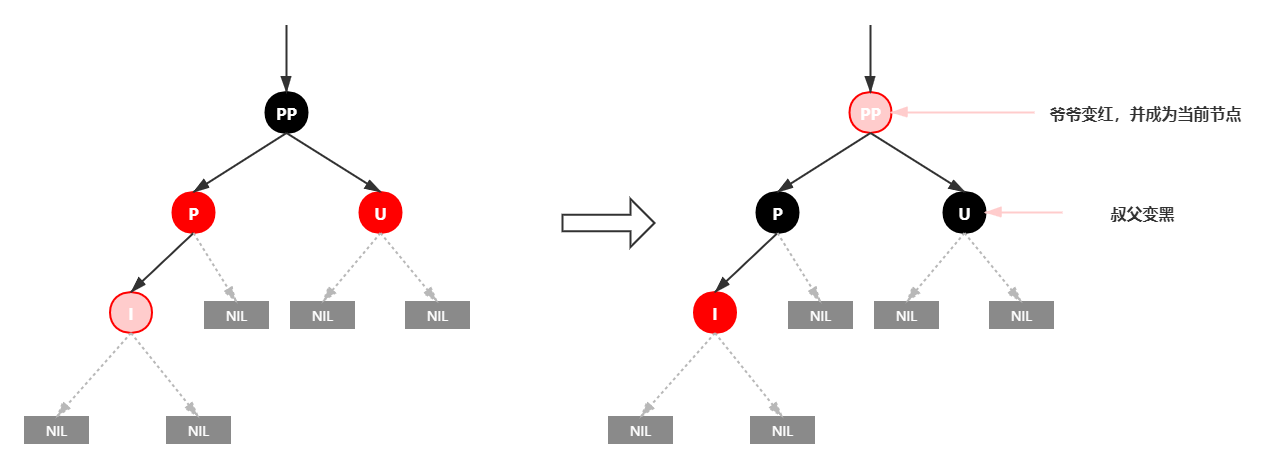
可以看到，我们把PP结点设为红色了，如果PP的父结点是黑色，那么无需再做任何处理；
但如果PP的父结点是红色，则违反红黑树性质了。所以需要将PP设置为当前节点，继续做插入操作自平衡处理，直到平衡为止

情景4.2：叔叔节点不存在，或者为黑色，父节点为爷爷节点的左子树

情景4.2.1：插入节点为其父节点的左子节点（LL情况）

处理：
1.变颜色：将P设置为黑色，将PP设置为红色
2.对PP节点进行右旋

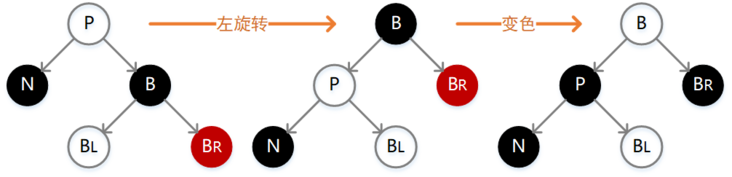
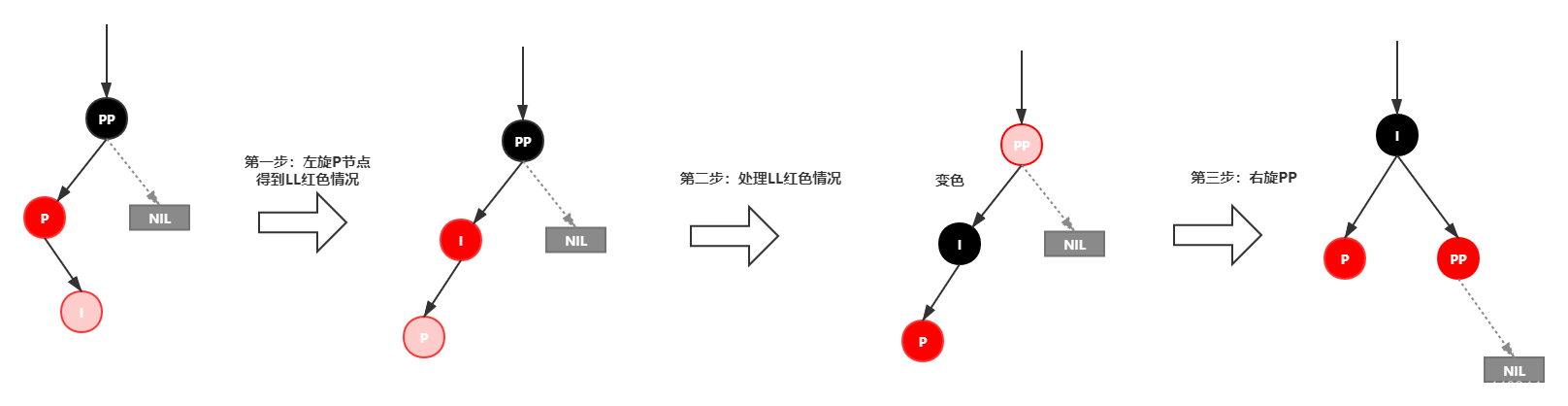
情景4.2.2：插入节点为其父节点的右子节点（LR情况）

处理：
1.对P进行左旋
2.将P设置为当前节点，得到LL红色情况
3.按照LL红色情况处理（1.变颜色 2.右旋PP）

情景4.3：叔叔节点不存在，或者为黑色，父节点为爷爷节点的右子树

情景4.3.1：插入节点为其父节点的右子节点（RR情况）

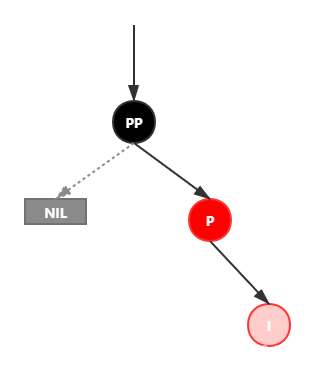
处理：
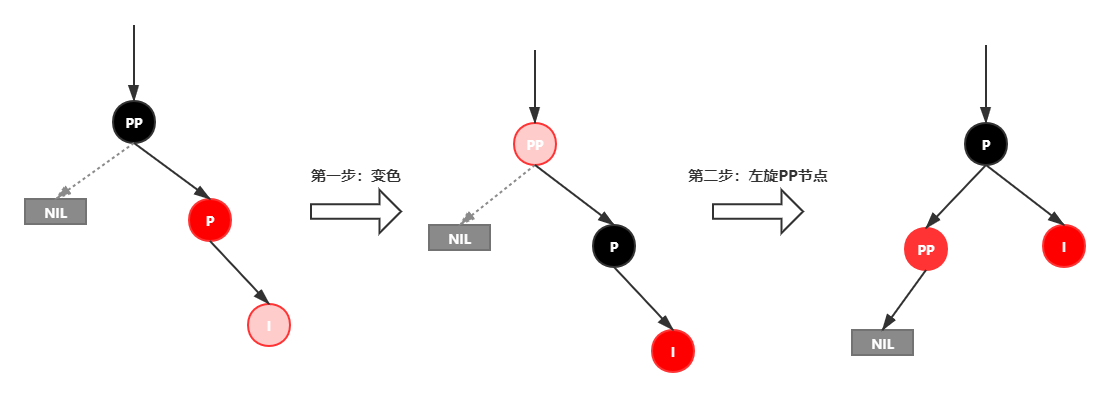
1.变颜色：将P设置为黑色，将PP设置为红色
2.对PP节点进行左旋

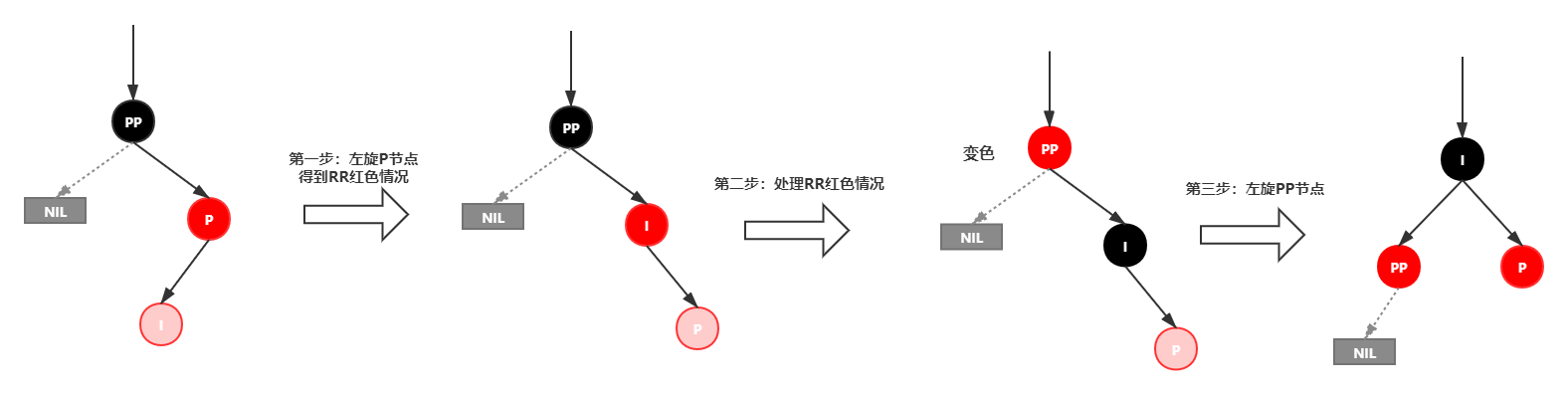
情景4.3.2：插入节点为其父节点的左子节点（RL情况）

处理：
1.对P进行右旋
2.将P设置为当前节点，得到RR红色情况
3.按照RR红色情况处理（1.变颜色 2.左旋PP）

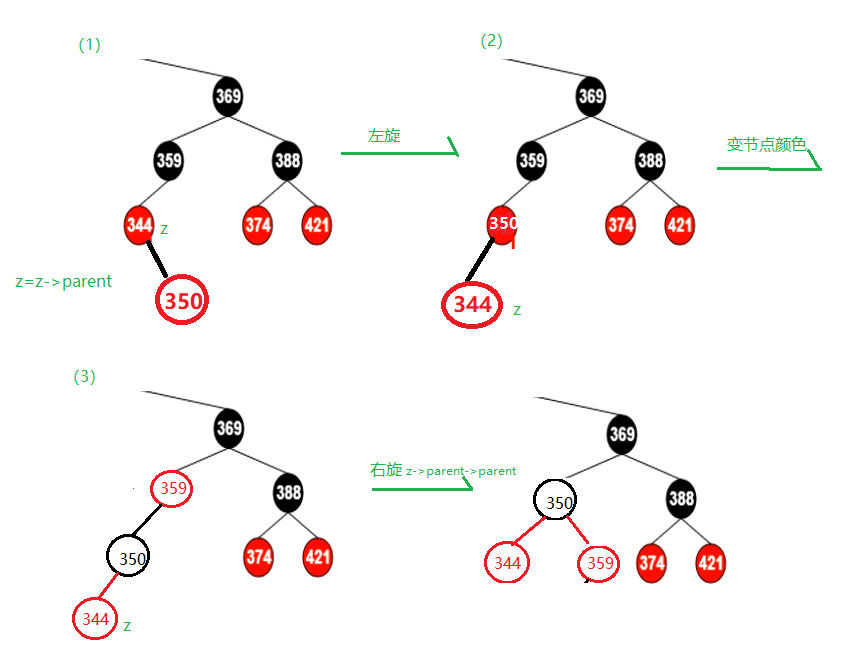
四、红黑树插入案例分析

把7插进红黑树

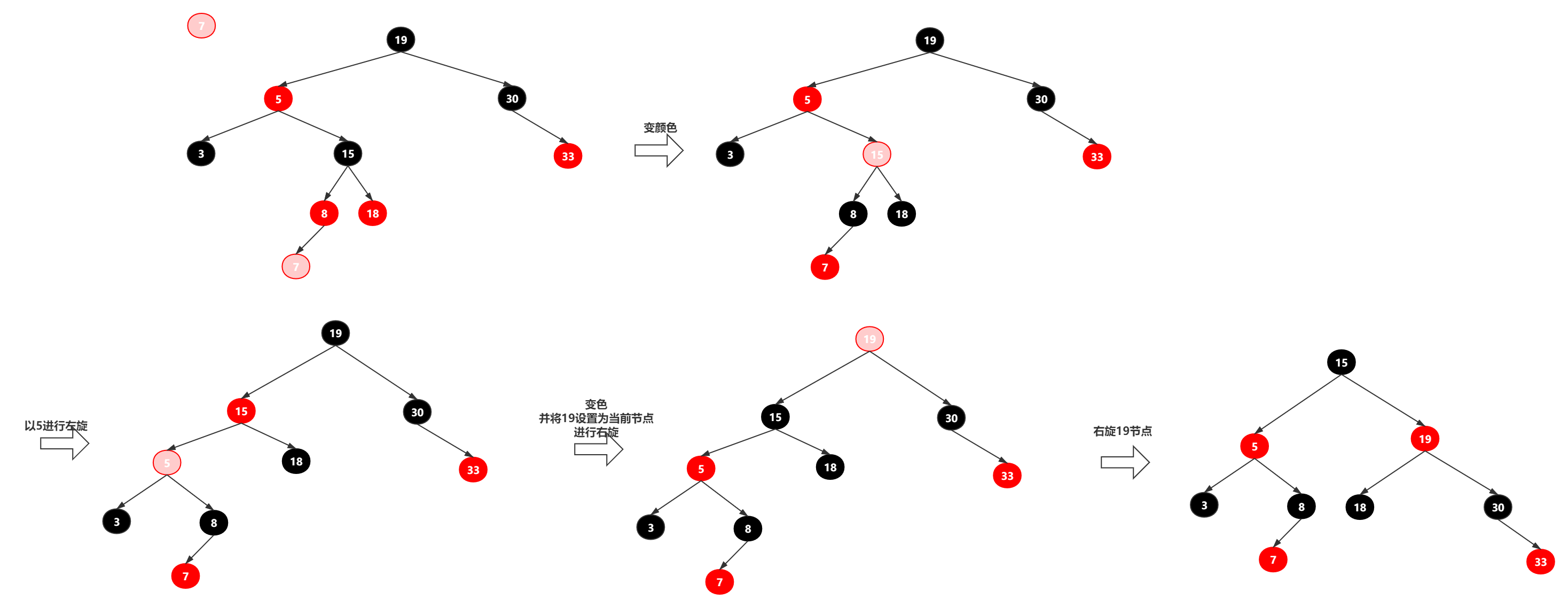
介绍了红黑树的理论，接下来就是手撕代码了
手写红黑树