红黑树原理及java实现

红黑树

在这里插入图片描述

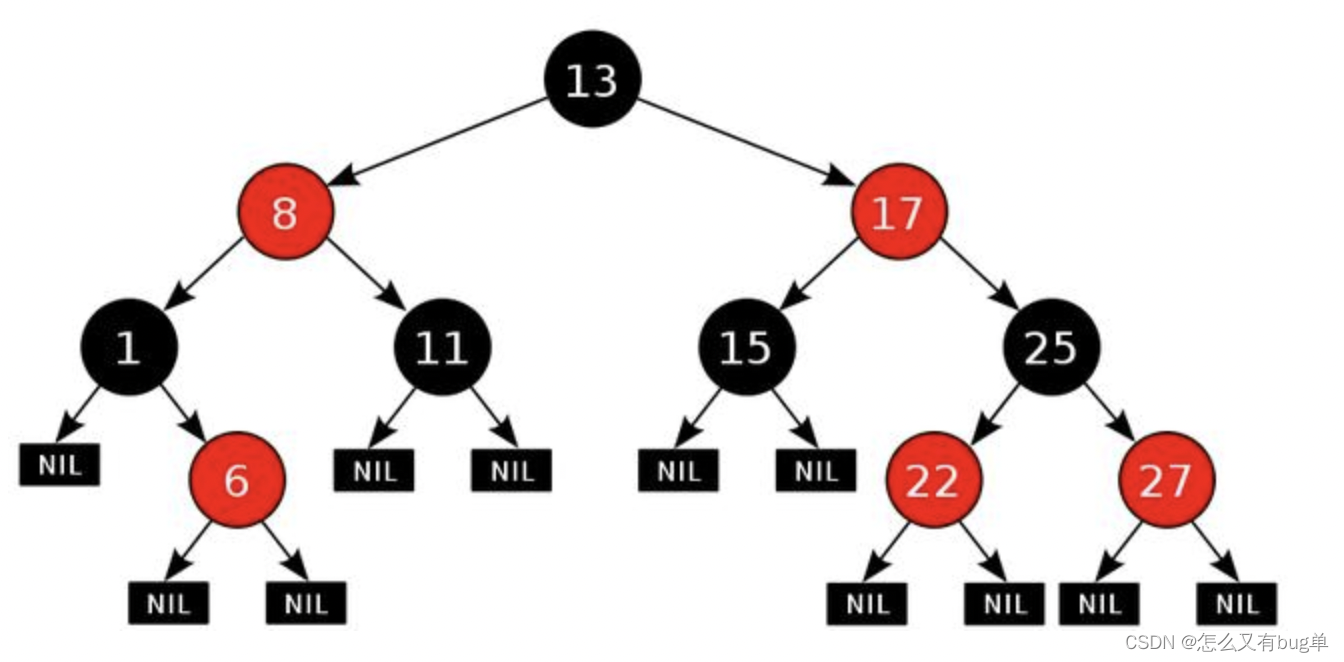
红黑树规则特点：

节点分为红色或者黑色；
根节点必为黑色；
叶子节点都为黑色，且为null；
连接红色节点的两个子节点都为黑色（红黑树不会出现相邻的红色节点）；
从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点；
新加入到红黑树的节点为红色节点；

红黑树的基本操作是添加、删除和旋转。在对红黑树进行添加或删除后，会用到旋转方法。

红黑树的查找, 添加, 删除都是O(logn)

红黑树常见用途:

1.Linux非实时任务调度中的应用

Linux 的稳定内核版本在 2． 6． 24 之后，使用了新的调度程序 CFS，所有非实时可运行进程都以虚拟运行时间为 key 值挂在一棵红黑树上，以完成更公平高效地调度所有任务。CFS 弃用 active /expired 数组和动态计算优先级，不再跟踪任务的睡眠时间和区别是否交互任务，并且在调度中采用基于时间计算键值的红黑树来选取下一个任务，根据所有任务占用 CPU 时间的状态来确定调度任务优先级。 [3]

2.Linux虚拟内存中的应用

32 位 Linux 内核虚拟地址空间划分 0 － 3G 为用户空间，3 － 4G 为内核空间，因此每个进程可以使用 4GB的虚拟空间。同时，Linux 定义了虚拟存储区域( VMA) 以便于更好表示进程所使用的虚拟空间，每个 VMA是某个进程的一段连续虚拟空间，其中的单元具有相同的特征，所有的虚拟区域按照地址排序由指针链接为一个链表。当发生缺页中断时搜索 VMA 到指定区域时，则需要频繁操作，因此选用了红黑树以减少查找时间。 [3]

3.检测树的平衡性上的应用

红黑树是一种自平衡二叉搜索树，它的每个结点都被“着色”为红色或者黑色，这些结点的颜色被用来检测树的平衡性。红黑树作为嵌入式数据库中的索引机制，可以获得更好的性能，对于SQLite数据库，可以采用红黑树实现索引机制的优化。 [6]

4. Java 的集合框架 (HashMap、TreeMap、TreeSet)

5. Nginx 的 Timer 管理

用红黑树管理timer,因为红黑树是有序的,可以很快的得到距离当前最小的定时器.

6. IO多路复用epoll的实现采用红黑树组织管理sockfd，以支持快速的增删改查.

7. C++的STL中，map和set是用红黑树实现的

以下是红黑树的具体实现:

1. 基本定义:

public class RBTree<T extends Comparable<T>> {private RBTNode<T> mRoot;    // 根结点private static final boolean RED   = false;private static final boolean BLACK = true;public class RBTNode<T extends Comparable<T>> {boolean color;        // 颜色T key;                // 关键字(键值)RBTNode<T> left;    // 左孩子RBTNode<T> right;    // 右孩子RBTNode<T> parent;    // 父结点public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {this.key = key;this.color = color;this.parent = parent;this.left = left;this.right = right;}}
}
...

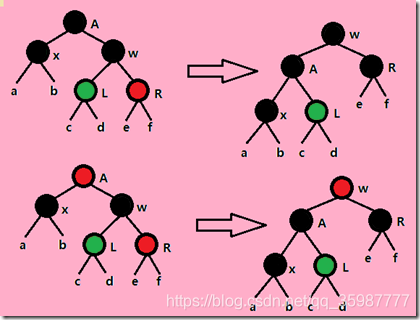
2. 左旋:

在这里插入图片描述

/* * 对红黑树的节点(x)进行左旋转** 左旋示意图(对节点x进行左旋)：*      px                              px*     /                               /*    x                               y                *   /  \      --(左旋)-.           / \                #*  lx   y                          x  ry     *     /   \                       /  \*    ly   ry                     lx  ly  ***/
private void leftRotate(RBTNode<T> x) {// 设置x的右孩子为yRBTNode<T> y = x.right;// 将 “y的左孩子” 设为 “x的右孩子”；// 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”x.right = y.left;if (y.left != null)y.left.parent = x;// 将 “x的父亲” 设为 “y的父亲”y.parent = x.parent;if (x.parent == null) {this.mRoot = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点} else {if (x.parent.left == x)x.parent.left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”elsex.parent.right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”}// 将 “x” 设为 “y的左孩子”y.left = x;// 将 “x的父节点” 设为 “y”x.parent = y;
}

3. 右旋:

在这里插入图片描述

/* * 对红黑树的节点(y)进行右旋转** 右旋示意图(对节点y进行左旋)：*            py                               py*           /                                /*          y                                x                  *         /  \      --(右旋)-.            /  \                     #*        x   ry                           lx   y  *       / \                                   / \                   #*      lx  rx                                rx  ry* */
private void rightRotate(RBTNode<T> y) {// 设置x是当前节点的左孩子。RBTNode<T> x = y.left;// 将 “x的右孩子” 设为 “y的左孩子”；// 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”y.left = x.right;if (x.right != null)x.right.parent = y;// 将 “y的父亲” 设为 “x的父亲”x.parent = y.parent;if (y.parent == null) {this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点} else {if (y == y.parent.right)y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”elsey.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”}// 将 “y” 设为 “x的右孩子”x.right = y;// 将 “y的父节点” 设为 “x”y.parent = x;
}

4. 添加

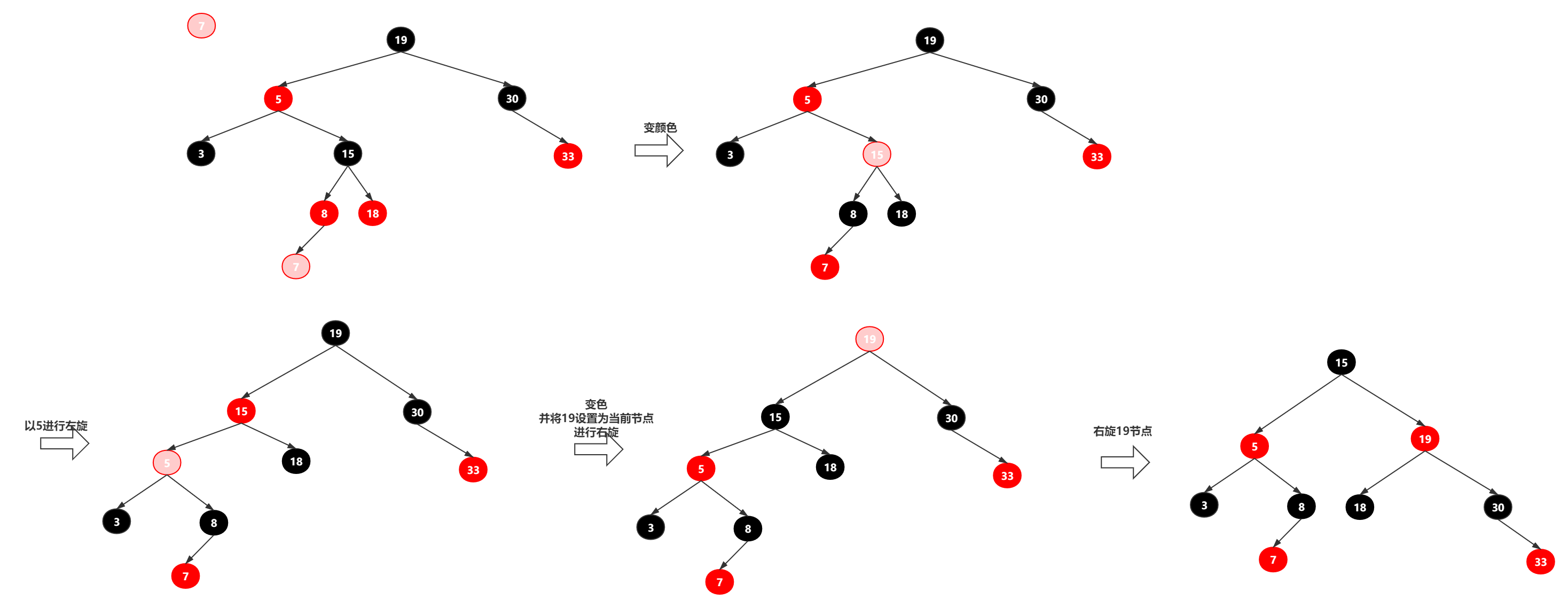
将一个节点插入到红黑树中，需要执行哪些步骤呢？首先，将红黑树当作一颗二叉查找树，将节点插入；然后，将节点着色为红色；最后，通过"旋转和重新着色"等一系列操作来修正该树，使之重新成为一颗红黑树。详细描述如下：
第一步: 将红黑树当作一颗二叉查找树，将节点插入。
红黑树本身就是一颗二叉查找树，将节点插入后，该树仍然是一颗二叉查找树。也就意味着，树的键值仍然是有序的。此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。这也就意味着，任何的旋转和重新着色操作，都不会改变它仍然是一颗二叉查找树的事实。
好吧？那接下来，我们就来想方设法的旋转以及重新着色，使这颗树重新成为红黑树！

第二步：将插入的节点着色为"红色"。
为什么着色成红色，而不是黑色呢？为什么呢？在回答之前，我们需要重新温习一下红黑树的特性：
(1) 每个节点或者是黑色，或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]
(4) 如果一个节点是红色的，则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
将插入的节点着色为红色，不会违背"特性(5)"！少违背一条特性，就意味着我们需要处理的情况越少。接下来，就要努力的让这棵树满足其它性质即可；满足了的话，它就又是一颗红黑树了。o(∩∩)o…哈哈

第三步: 通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。
第二步中，将插入节点着色为"红色"之后，不会违背"特性(5)"。那它到底会违背哪些特性呢？
对于"特性(1)"，显然不会违背了。因为我们已经将它涂成红色了。
对于"特性(2)"，显然也不会违背。在第一步中，我们是将红黑树当作二叉查找树，然后执行的插入操作。而根据二叉查找数的特点，插入操作不会改变根节点。所以，根节点仍然是黑色。
对于"特性(3)"，显然不会违背了。这里的叶子节点是指的空叶子节点，插入非空节点并不会对它们造成影响。
对于"特性(4)"，是有可能违背的！
那接下来，想办法使之"满足特性(4)"，就可以将树重新构造成红黑树了。

/* * 将结点插入到红黑树中** 参数说明：*     node 插入的结点        // 对应《算法导论》中的node*/
private void insert(RBTNode<T> node) {int cmp;RBTNode<T> y = null;RBTNode<T> x = this.mRoot;// 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。while (x != null) {y = x;cmp = node.key.compareTo(x.key);if (cmp < 0)x = x.left;elsex = x.right;}node.parent = y;if (y!=null) {cmp = node.key.compareTo(y.key);if (cmp < 0)y.left = node;elsey.right = node;} else {this.mRoot = node;}// 2. 设置节点的颜色为红色node.color = RED;// 3. 将它重新修正为一颗二叉查找树insertFixUp(node);
}/* * 新建结点(key)，并将其插入到红黑树中** 参数说明：*     key 插入结点的键值*/
public void insert(T key) {RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);// 如果新建结点失败，则返回。if (node != null)insert(node);
}

内部接口 – insert(node)的作用是将"node"节点插入到红黑树中。
外部接口 – insert(key)的作用是将"key"添加到红黑树中。

添加修正操作的实现代码:

/** 红黑树插入修正函数** 在向红黑树中插入节点之后(失去平衡)，再调用该函数；* 目的是将它重新塑造成一颗红黑树。** 参数说明：*     node 插入的结点        // 对应《算法导论》中的z*/
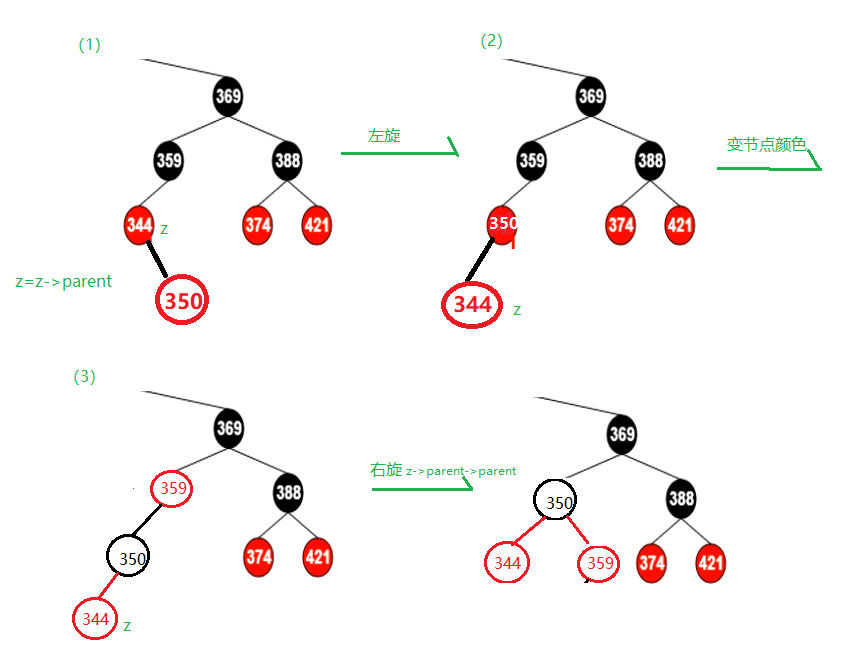
private void insertFixUp(RBTNode<T> node) {RBTNode<T> parent, gparent;// 若“父节点存在，并且父节点的颜色是红色”while (((parent = parentOf(node))!=null) && isRed(parent)) {gparent = parentOf(parent);//若“父节点”是“祖父节点的左孩子”if (parent == gparent.left) {// Case 1条件：叔叔节点是红色RBTNode<T> uncle = gparent.right;if ((uncle!=null) && isRed(uncle)) {setBlack(uncle);setBlack(parent);setRed(gparent);node = gparent;continue;}// Case 2条件：叔叔是黑色，且当前节点是右孩子if (parent.right == node) {RBTNode<T> tmp;leftRotate(parent);tmp = parent;parent = node;node = tmp;}// Case 3条件：叔叔是黑色，且当前节点是左孩子。setBlack(parent);setRed(gparent);rightRotate(gparent);} else {    //若“z的父节点”是“z的祖父节点的右孩子”// Case 1条件：叔叔节点是红色RBTNode<T> uncle = gparent.left;if ((uncle!=null) && isRed(uncle)) {setBlack(uncle);setBlack(parent);setRed(gparent);node = gparent;continue;}// Case 2条件：叔叔是黑色，且当前节点是左孩子if (parent.left == node) {RBTNode<T> tmp;rightRotate(parent);tmp = parent;parent = node;node = tmp;}// Case 3条件：叔叔是黑色，且当前节点是右孩子。setBlack(parent);setRed(gparent);leftRotate(gparent);}}// 将根节点设为黑色setBlack(this.mRoot);
}

5. 删除

将红黑树内的某一个节点删除。需要执行的操作依次是：首先，将红黑树当作一颗二叉查找树，将该节点从二叉查找树中删除；然后，通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。详细描述如下：
第一步：将红黑树当作一颗二叉查找树，将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况：
① 被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么，先找出它的后继节点；然后把“它的后继节点的内容”复制给“该节点的内容”；之后，删除“它的后继节点”。在这里，后继节点相当于替身，在将后继节点的内容复制给"被删除节点"之后，再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了，下面就考虑后继节点。在"被删除节点"有两个非空子节点的情况下，它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空，就意味着"该节点的后继节点"要么没有儿子，要么只有一个儿子。若没有儿子，则按"情况① "进行处理；若只有一个儿子，则按"情况② "进行处理。

第二步：通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。
因为"第一步"中删除节点之后，可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树，使之重新成为一棵红黑树。

/* * 删除结点(node)，并返回被删除的结点** 参数说明：*     node 删除的结点*/
private void remove(RBTNode<T> node) {RBTNode<T> child, parent;boolean color;// 被删除节点的"左右孩子都不为空"的情况。if ( (node.left!=null) && (node.right!=null) ) {// 被删节点的后继节点。(称为"取代节点")// 用它来取代"被删节点"的位置，然后再将"被删节点"去掉。RBTNode<T> replace = node;// 获取后继节点replace = replace.right;while (replace.left != null)replace = replace.left;// "node节点"不是根节点(只有根节点不存在父节点)if (parentOf(node)!=null) {if (parentOf(node).left == node)parentOf(node).left = replace;elseparentOf(node).right = replace;} else {// "node节点"是根节点，更新根节点。this.mRoot = replace;}// child是"取代节点"的右孩子，也是需要"调整的节点"。// "取代节点"肯定不存在左孩子！因为它是一个后继节点。child = replace.right;parent = parentOf(replace);// 保存"取代节点"的颜色color = colorOf(replace);// "被删除节点"是"它的后继节点的父节点"if (parent == node) {parent = replace;} else {// child不为空if (child!=null)setParent(child, parent);parent.left = child;replace.right = node.right;setParent(node.right, replace);}replace.parent = node.parent;replace.color = node.color;replace.left = node.left;node.left.parent = replace;if (color == BLACK)removeFixUp(child, parent);node = null;return ;}if (node.left !=null) {child = node.left;} else {child = node.right;}parent = node.parent;// 保存"取代节点"的颜色color = node.color;if (child!=null)child.parent = parent;// "node节点"不是根节点if (parent!=null) {if (parent.left == node)parent.left = child;elseparent.right = child;} else {this.mRoot = child;}if (color == BLACK)removeFixUp(child, parent);node = null;
}/* * 删除结点(z)，并返回被删除的结点** 参数说明：*     tree 红黑树的根结点*     z 删除的结点*/
public void remove(T key) {RBTNode<T> node; if ((node = search(mRoot, key)) != null)remove(node);
}

内部接口 – remove(node)的作用是将"node"节点插入到红黑树中。
外部接口 – remove(key)删除红黑树中键值为key的节点。

删除修正操作的实现代码(Java语言)

/** 红黑树删除修正函数** 在从红黑树中删除插入节点之后(红黑树失去平衡)，再调用该函数；* 目的是将它重新塑造成一颗红黑树。** 参数说明：*     node 待修正的节点*/
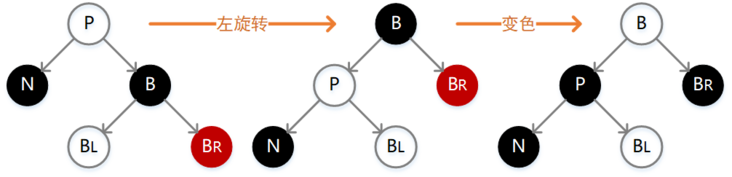
private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {RBTNode<T> other;while ((node==null || isBlack(node)) && (node != this.mRoot)) {if (parent.left == node) {other = parent.right;if (isRed(other)) {// Case 1: x的兄弟w是红色的  setBlack(other);setRed(parent);leftRotate(parent);other = parent.right;}if ((other.left==null || isBlack(other.left)) &&(other.right==null || isBlack(other.right))) {// Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的  setRed(other);node = parent;parent = parentOf(node);} else {if (other.right==null || isBlack(other.right)) {// Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。  setBlack(other.left);setRed(other);rightRotate(other);other = parent.right;}// Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。setColor(other, colorOf(parent));setBlack(parent);setBlack(other.right);leftRotate(parent);node = this.mRoot;break;}} else {other = parent.left;if (isRed(other)) {// Case 1: x的兄弟w是红色的  setBlack(other);setRed(parent);rightRotate(parent);other = parent.left;}if ((other.left==null || isBlack(other.left)) &&(other.right==null || isBlack(other.right))) {// Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的  setRed(other);node = parent;parent = parentOf(node);} else {if (other.left==null || isBlack(other.left)) {// Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。  setBlack(other.right);setRed(other);leftRotate(other);other = parent.left;}// Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。setColor(other, colorOf(parent));setBlack(parent);setBlack(other.left);rightRotate(parent);node = this.mRoot;break;}}}if (node!=null)setBlack(node);
}

6. 详细代码:


public class RBTree<T extends Comparable<T>> {private RBTNode<T> mRoot;    // 根结点private static final boolean RED   = false;private static final boolean BLACK = true;public class RBTNode<T extends Comparable<T>> {boolean color;        // 颜色T key;                // 关键字(键值)RBTNode<T> left;    // 左孩子RBTNode<T> right;    // 右孩子RBTNode<T> parent;    // 父结点public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {this.key = key;this.color = color;this.parent = parent;this.left = left;this.right = right;}public T getKey() {return key;}public String toString() {return ""+key+(this.color==RED?"(R)":"B");}}public RBTree() {mRoot=null;}private RBTNode<T> parentOf(RBTNode<T> node) {return node!=null ? node.parent : null;}private boolean colorOf(RBTNode<T> node) {return node!=null ? node.color : BLACK;}private boolean isRed(RBTNode<T> node) {return ((node!=null)&&(node.color==RED)) ? true : false;}private boolean isBlack(RBTNode<T> node) {return !isRed(node);}private void setBlack(RBTNode<T> node) {if (node!=null)node.color = BLACK;}private void setRed(RBTNode<T> node) {if (node!=null)node.color = RED;}private void setParent(RBTNode<T> node, RBTNode<T> parent) {if (node!=null)node.parent = parent;}private void setColor(RBTNode<T> node, boolean color) {if (node!=null)node.color = color;}/** 前序遍历"红黑树"*/private void preOrder(RBTNode<T> tree) {if(tree != null) {System.out.print(tree.key+" ");preOrder(tree.left);preOrder(tree.right);}}public void preOrder() {preOrder(mRoot);}/** 中序遍历"红黑树"*/private void inOrder(RBTNode<T> tree) {if(tree != null) {inOrder(tree.left);System.out.print(tree.key+" ");inOrder(tree.right);}}public void inOrder() {inOrder(mRoot);}/** 后序遍历"红黑树"*/private void postOrder(RBTNode<T> tree) {if(tree != null){postOrder(tree.left);postOrder(tree.right);System.out.print(tree.key+" ");}}public void postOrder() {postOrder(mRoot);}/** (递归实现)查找"红黑树x"中键值为key的节点*/private RBTNode<T> search(RBTNode<T> x, T key) {if (x==null)return x;int cmp = key.compareTo(x.key);if (cmp < 0)return search(x.left, key);else if (cmp > 0)return search(x.right, key);elsereturn x;}public RBTNode<T> search(T key) {return search(mRoot, key);}/** (非递归实现)查找"红黑树x"中键值为key的节点*/private RBTNode<T> iterativeSearch(RBTNode<T> x, T key) {while (x!=null) {int cmp = key.compareTo(x.key);if (cmp < 0)x = x.left;else if (cmp > 0)x = x.right;elsereturn x;}return x;}public RBTNode<T> iterativeSearch(T key) {return iterativeSearch(mRoot, key);}/** 查找最小结点：返回tree为根结点的红黑树的最小结点。*/private RBTNode<T> minimum(RBTNode<T> tree) {if (tree == null)return null;while(tree.left != null)tree = tree.left;return tree;}public T minimum() {RBTNode<T> p = minimum(mRoot);if (p != null)return p.key;return null;}/** 查找最大结点：返回tree为根结点的红黑树的最大结点。*/private RBTNode<T> maximum(RBTNode<T> tree) {if (tree == null)return null;while(tree.right != null)tree = tree.right;return tree;}public T maximum() {RBTNode<T> p = maximum(mRoot);if (p != null)return p.key;return null;}/** 找结点(x)的后继结点。即，查找"红黑树中数据值大于该结点"的"最小结点"。*/public RBTNode<T> successor(RBTNode<T> x) {// 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。if (x.right != null)return minimum(x.right);// 如果x没有右孩子。则x有以下两种可能：// (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。// (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。RBTNode<T> y = x.parent;while ((y!=null) && (x==y.right)) {x = y;y = y.parent;}return y;}/** 找结点(x)的前驱结点。即，查找"红黑树中数据值小于该结点"的"最大结点"。*/public RBTNode<T> predecessor(RBTNode<T> x) {// 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。if (x.left != null)return maximum(x.left);// 如果x没有左孩子。则x有以下两种可能：// (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。// (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。RBTNode<T> y = x.parent;while ((y!=null) && (x==y.left)) {x = y;y = y.parent;}return y;}/** 对红黑树的节点(x)进行左旋转** 左旋示意图(对节点x进行左旋)：*      px                              px*     /                               /*    x                               y*   /  \      --(左旋)-.           / \                #*  lx   y                          x  ry*     /   \                       /  \*    ly   ry                     lx  ly***/private void leftRotate(RBTNode<T> x) {// 设置x的右孩子为yRBTNode<T> y = x.right;// 将 “y的左孩子” 设为 “x的右孩子”；// 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”x.right = y.left;if (y.left != null)y.left.parent = x;// 将 “x的父亲” 设为 “y的父亲”y.parent = x.parent;if (x.parent == null) {this.mRoot = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点} else {if (x.parent.left == x)x.parent.left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”elsex.parent.right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”}// 将 “x” 设为 “y的左孩子”y.left = x;// 将 “x的父节点” 设为 “y”x.parent = y;}/** 对红黑树的节点(y)进行右旋转** 右旋示意图(对节点y进行左旋)：*            py                               py*           /                                /*          y                                x*         /  \      --(右旋)-.            /  \                     #*        x   ry                           lx   y*       / \                                   / \                   #*      lx  rx                                rx  ry**/private void rightRotate(RBTNode<T> y) {// 设置x是当前节点的左孩子。RBTNode<T> x = y.left;// 将 “x的右孩子” 设为 “y的左孩子”；// 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”y.left = x.right;if (x.right != null)x.right.parent = y;// 将 “y的父亲” 设为 “x的父亲”x.parent = y.parent;if (y.parent == null) {this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点} else {if (y == y.parent.right)y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”elsey.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”}// 将 “y” 设为 “x的右孩子”x.right = y;// 将 “y的父节点” 设为 “x”y.parent = x;}/** 红黑树插入修正函数** 在向红黑树中插入节点之后(失去平衡)，再调用该函数；* 目的是将它重新塑造成一颗红黑树。** 参数说明：*     node 插入的结点        // 对应《算法导论》中的z*/private void insertFixUp(RBTNode<T> node) {RBTNode<T> parent, gparent;// 若“父节点存在，并且父节点的颜色是红色”while (((parent = parentOf(node))!=null) && isRed(parent)) {gparent = parentOf(parent);//若“父节点”是“祖父节点的左孩子”if (parent == gparent.left) {// Case 1条件：叔叔节点是红色RBTNode<T> uncle = gparent.right;if ((uncle!=null) && isRed(uncle)) {setBlack(uncle);setBlack(parent);setRed(gparent);node = gparent;continue;}// Case 2条件：叔叔是黑色，且当前节点是右孩子if (parent.right == node) {RBTNode<T> tmp;leftRotate(parent);tmp = parent;parent = node;node = tmp;}// Case 3条件：叔叔是黑色，且当前节点是左孩子。setBlack(parent);setRed(gparent);rightRotate(gparent);} else {    //若“z的父节点”是“z的祖父节点的右孩子”// Case 1条件：叔叔节点是红色RBTNode<T> uncle = gparent.left;if ((uncle!=null) && isRed(uncle)) {setBlack(uncle);setBlack(parent);setRed(gparent);node = gparent;continue;}// Case 2条件：叔叔是黑色，且当前节点是左孩子if (parent.left == node) {RBTNode<T> tmp;rightRotate(parent);tmp = parent;parent = node;node = tmp;}// Case 3条件：叔叔是黑色，且当前节点是右孩子。setBlack(parent);setRed(gparent);leftRotate(gparent);}}// 将根节点设为黑色setBlack(this.mRoot);}/** 将结点插入到红黑树中** 参数说明：*     node 插入的结点        // 对应《算法导论》中的node*/private void insert(RBTNode<T> node) {int cmp;RBTNode<T> y = null;RBTNode<T> x = this.mRoot;// 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。while (x != null) {y = x;cmp = node.key.compareTo(x.key);if (cmp < 0)x = x.left;elsex = x.right;}node.parent = y;if (y!=null) {cmp = node.key.compareTo(y.key);if (cmp < 0)y.left = node;elsey.right = node;} else {this.mRoot = node;}// 2. 设置节点的颜色为红色node.color = RED;// 3. 将它重新修正为一颗二叉查找树insertFixUp(node);}/** 新建结点(key)，并将其插入到红黑树中** 参数说明：*     key 插入结点的键值*/public void insert(T key) {RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);// 如果新建结点失败，则返回。if (node != null)insert(node);}/** 红黑树删除修正函数** 在从红黑树中删除插入节点之后(红黑树失去平衡)，再调用该函数；* 目的是将它重新塑造成一颗红黑树。** 参数说明：*     node 待修正的节点*/private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {RBTNode<T> other;while ((node==null || isBlack(node)) && (node != this.mRoot)) {if (parent.left == node) {other = parent.right;if (isRed(other)) {// Case 1: x的兄弟w是红色的setBlack(other);setRed(parent);leftRotate(parent);other = parent.right;}if ((other.left==null || isBlack(other.left)) &&(other.right==null || isBlack(other.right))) {// Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的setRed(other);node = parent;parent = parentOf(node);} else {if (other.right==null || isBlack(other.right)) {// Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。setBlack(other.left);setRed(other);rightRotate(other);other = parent.right;}// Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。setColor(other, colorOf(parent));setBlack(parent);setBlack(other.right);leftRotate(parent);node = this.mRoot;break;}} else {other = parent.left;if (isRed(other)) {// Case 1: x的兄弟w是红色的setBlack(other);setRed(parent);rightRotate(parent);other = parent.left;}if ((other.left==null || isBlack(other.left)) &&(other.right==null || isBlack(other.right))) {// Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的setRed(other);node = parent;parent = parentOf(node);} else {if (other.left==null || isBlack(other.left)) {// Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。setBlack(other.right);setRed(other);leftRotate(other);other = parent.left;}// Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。setColor(other, colorOf(parent));setBlack(parent);setBlack(other.left);rightRotate(parent);node = this.mRoot;break;}}}if (node!=null)setBlack(node);}/** 删除结点(node)，并返回被删除的结点** 参数说明：*     node 删除的结点*/private void remove(RBTNode<T> node) {RBTNode<T> child, parent;boolean color;// 被删除节点的"左右孩子都不为空"的情况。if ( (node.left!=null) && (node.right!=null) ) {// 被删节点的后继节点。(称为"取代节点")// 用它来取代"被删节点"的位置，然后再将"被删节点"去掉。RBTNode<T> replace = node;// 获取后继节点replace = replace.right;while (replace.left != null)replace = replace.left;// "node节点"不是根节点(只有根节点不存在父节点)if (parentOf(node)!=null) {if (parentOf(node).left == node)parentOf(node).left = replace;elseparentOf(node).right = replace;} else {// "node节点"是根节点，更新根节点。this.mRoot = replace;}// child是"取代节点"的右孩子，也是需要"调整的节点"。// "取代节点"肯定不存在左孩子！因为它是一个后继节点。child = replace.right;parent = parentOf(replace);// 保存"取代节点"的颜色color = colorOf(replace);// "被删除节点"是"它的后继节点的父节点"if (parent == node) {parent = replace;} else {// child不为空if (child!=null)setParent(child, parent);parent.left = child;replace.right = node.right;setParent(node.right, replace);}replace.parent = node.parent;replace.color = node.color;replace.left = node.left;node.left.parent = replace;if (color == BLACK)removeFixUp(child, parent);node = null;return ;}if (node.left !=null) {child = node.left;} else {child = node.right;}parent = node.parent;// 保存"取代节点"的颜色color = node.color;if (child!=null)child.parent = parent;// "node节点"不是根节点if (parent!=null) {if (parent.left == node)parent.left = child;elseparent.right = child;} else {this.mRoot = child;}if (color == BLACK)removeFixUp(child, parent);node = null;}/** 删除结点(z)，并返回被删除的结点** 参数说明：*     tree 红黑树的根结点*     z 删除的结点*/public void remove(T key) {RBTNode<T> node;if ((node = search(mRoot, key)) != null)remove(node);}/** 销毁红黑树*/private void destroy(RBTNode<T> tree) {if (tree==null)return ;if (tree.left != null)destroy(tree.left);if (tree.right != null)destroy(tree.right);tree=null;}public void clear() {destroy(mRoot);mRoot = null;}/** 打印"红黑树"** key        -- 节点的键值* direction  --  0，表示该节点是根节点;*               -1，表示该节点是它的父结点的左孩子;*                1，表示该节点是它的父结点的右孩子。*/private void print(RBTNode<T> tree, T key, int direction) {if(tree != null) {if(direction==0)    // tree是根节点System.out.printf("%2d(B) is root\n", tree.key);else                // tree是分支节点System.out.printf("%2d(%s) is %2d's %6s child\n", tree.key, isRed(tree)?"R":"B", key, direction==1?"right" : "left");print(tree.left, tree.key, -1);print(tree.right,tree.key,  1);}}public void print() {if (mRoot != null)print(mRoot, mRoot.key, 0);}
}