前言

在阅读HashMap源码的时候发现，java1.8的HashMap的链表实现增加了红黑树，当链表长度超过指定阈值8的时候回进行树化。
为了提高增删查的效率。
而红黑树又比较复杂，所以专门写一篇关于红黑树的文章。

概念

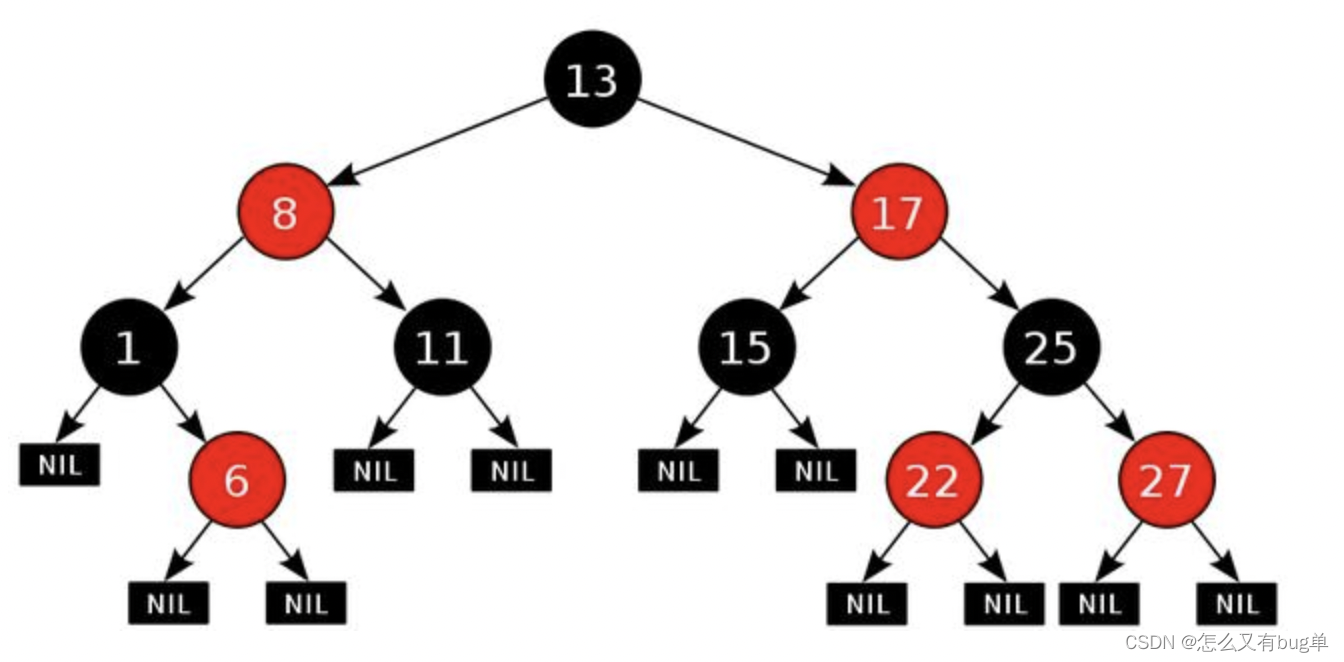
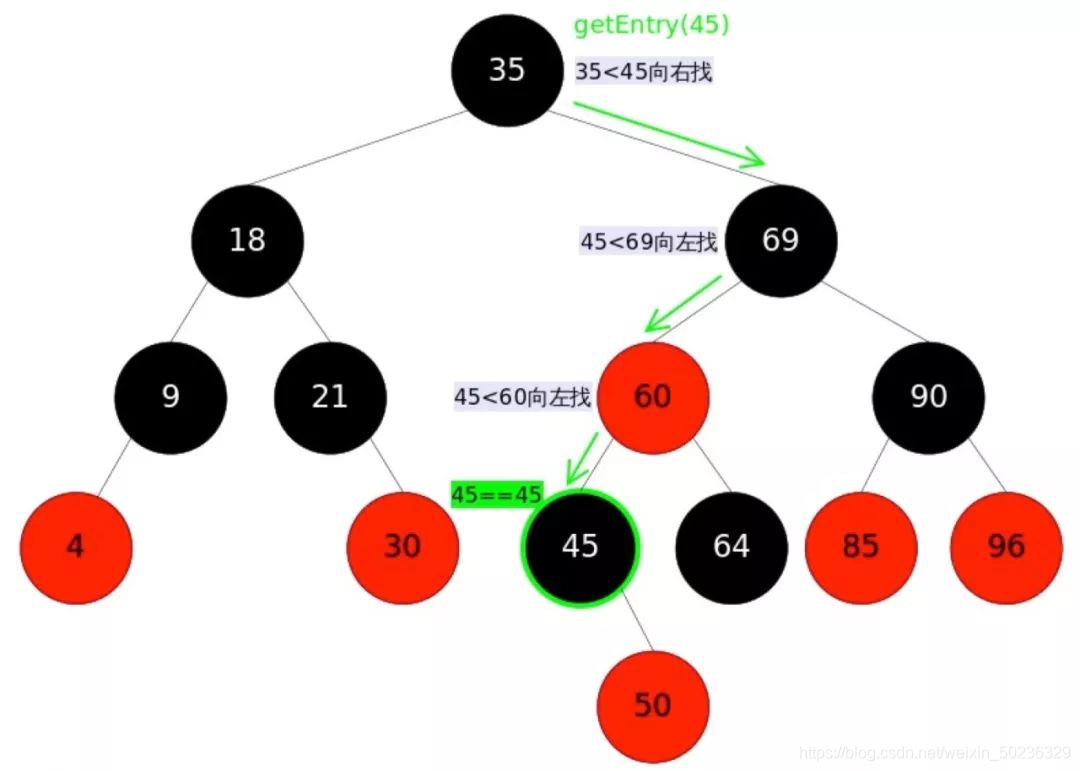
R-B Tree，全称是Red-Black Tree，又称为“红黑树”，是一种特殊的二叉查找树。红黑树的每个结点上都有存储位表示结点的颜色， 可以是红(Red)或黑(Black)。
了解一下百度给出的红黑树概念：
摘自百度：
      红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。
在了解红黑树之前，先了解一下AVL树： AVL树
红黑树的统计功能要好于AVL树，因为AVL是严格平衡的，红黑树是黑平衡的，维持平衡需要额外的操作。

应用

• C++的STL，map和set都是用红黑树实现的。

• 著名的linux进程调度Completely Fair Scheduler，用红黑树管理进程控制块。

• epoll在内核中的实现，用红黑树管理事件块。

• nginx用红黑树管理timer等。

• Java的TreeMap实现。

性质

红黑树不仅是自平衡二叉树还满足5个性质：
1）每个结点或红或黑
2）根结点是黑色
3）空叶子结点是黑色
4）如果一个结点是红色，那么它的子节点是黑色
5）从任意一个结点出发到空的叶子结点经过的黑结点个数相同
为了满足这五个性质，对于平衡二叉树的插入，删除就多增加了一些操作，
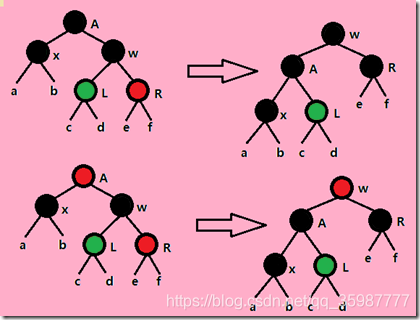
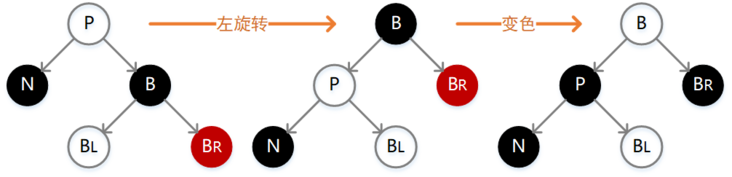
左旋，右旋，变色：

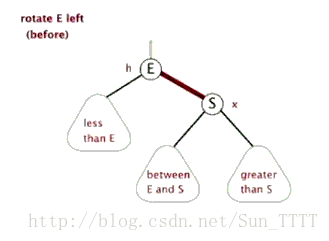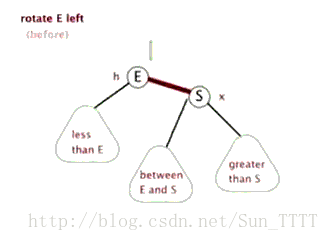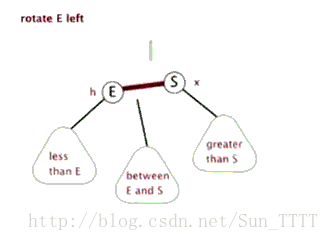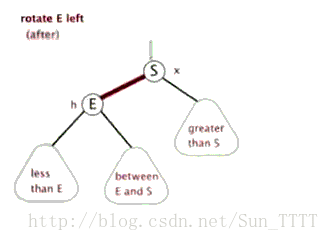
• 左旋
  以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，其左子结点保持不变
  如图：
  
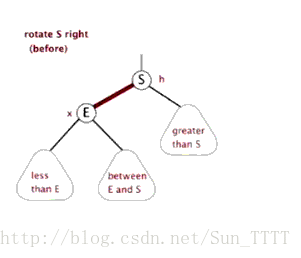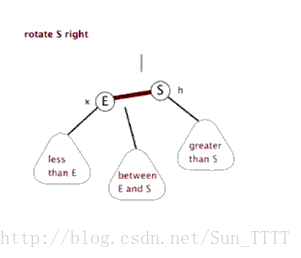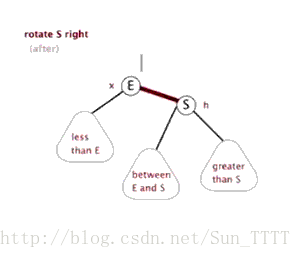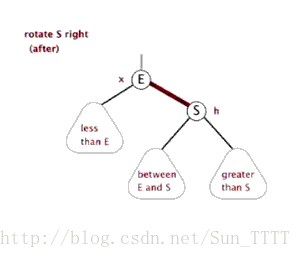
• 右旋
  以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，其右子结点保持不变。
  如图：
  

操作

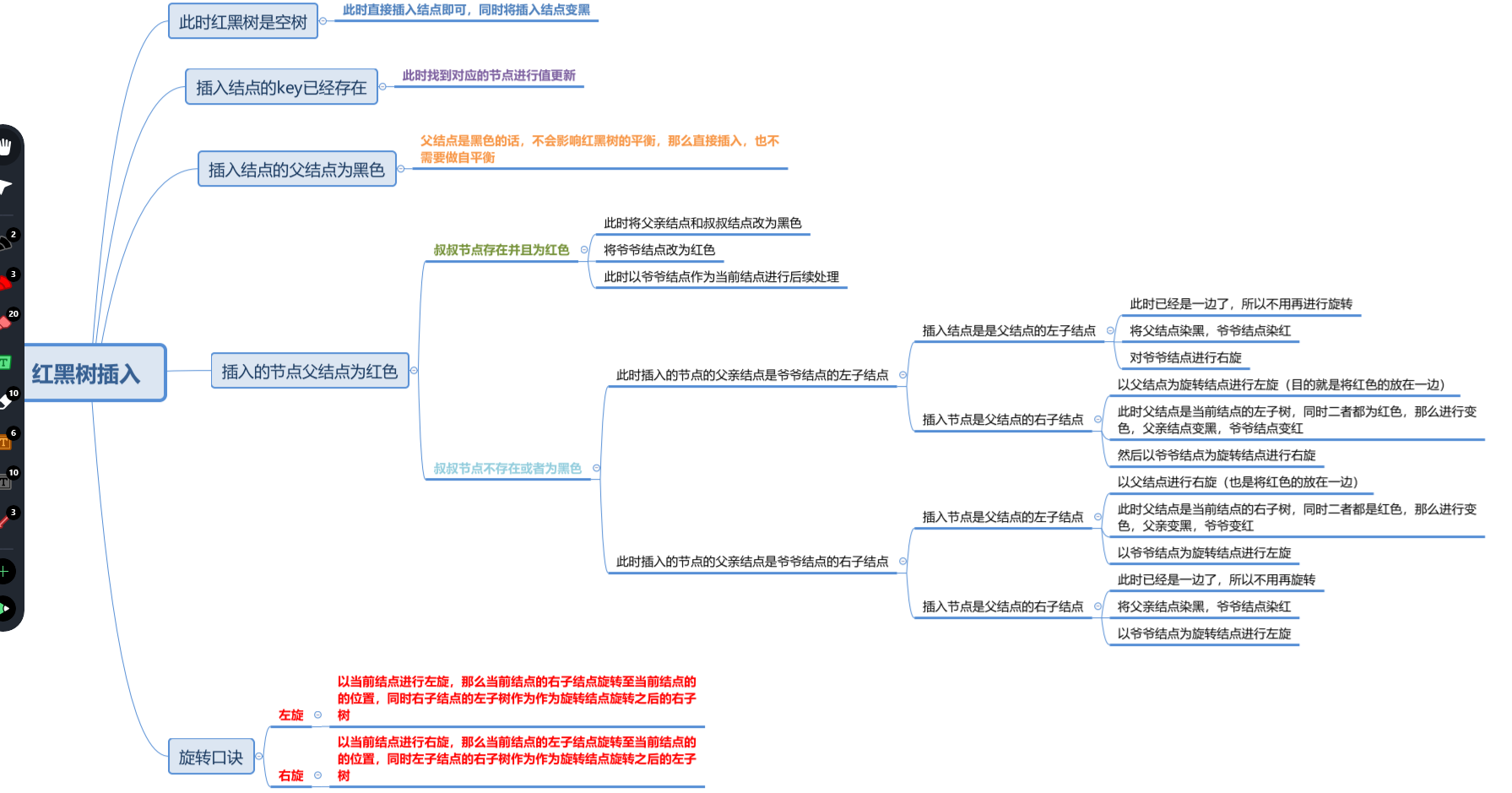
• 插入
  插入节点面临的情况：
  1.树为空，插入的结点为根结点
  直接将插入的结点变成黑色

  
  2.父亲结点为黑色结点
  不需要任何操作,直接插入89就可以了。
  
  3.父亲结点为红色结点的情况下：
  3.1 叔叔节点为黑色的情况（叔叔节点不存在即为黑色）
  3.1.1 父亲结点为右孩子，插入结点为左孩子
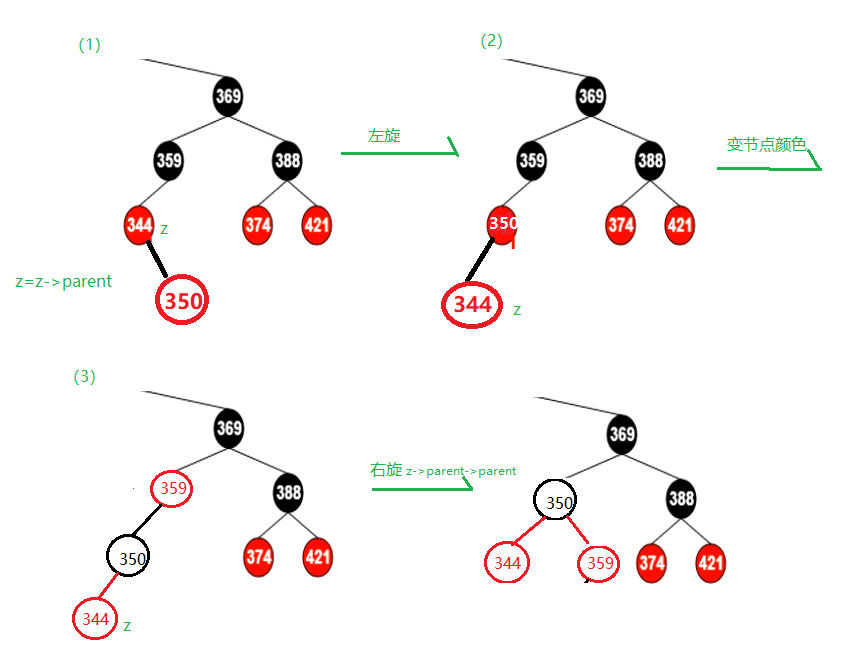
  针对父结点进行右旋，此时右旋后的情况必定是3.1.3的情况，然后按照3.1.3的情况处理;
  
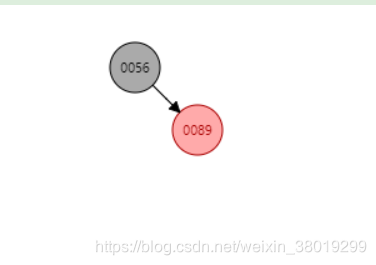
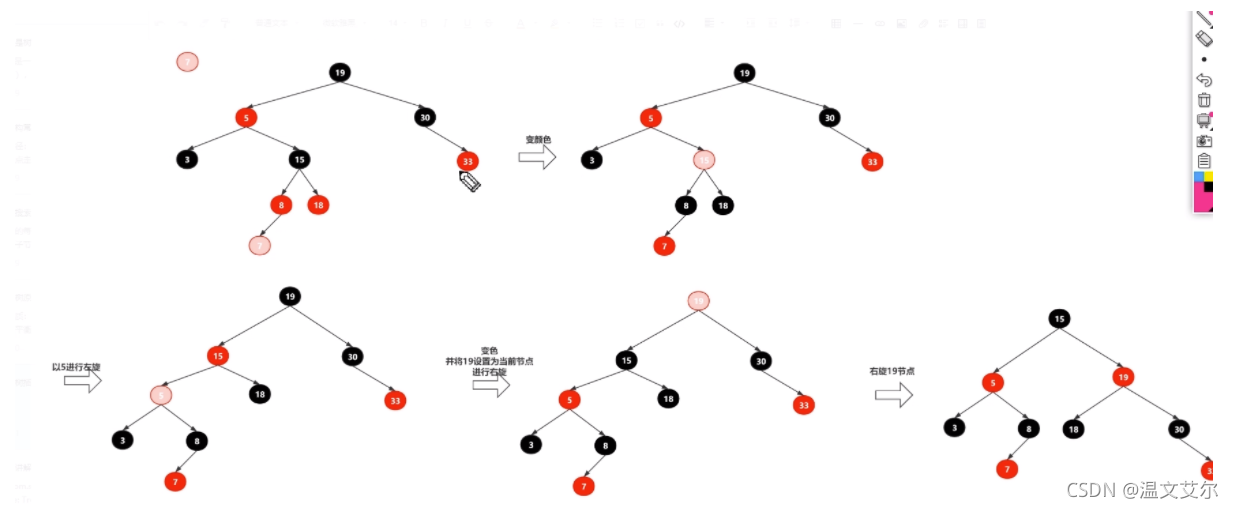
  如图插入80以后变成这样了，按照上面的结论，先将80和89以89结点进行右旋，右旋后80变89的父节点，89为80的右孩子结点，此时的情况就是3.1.3情况，进行操作，将80和56颜色互换，然后对56进行左旋。此时就是上图的样子了。
  3.1.2 父亲结点为左孩子，插入结点为右孩子
  针对父节点进行左旋，此时左旋后的情况为3.1.4情况，然后按照3.1.4进行操作。
  
  
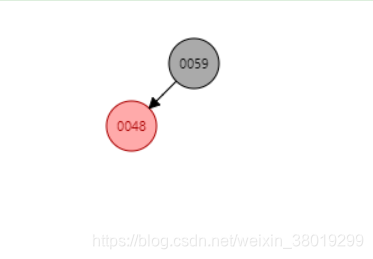
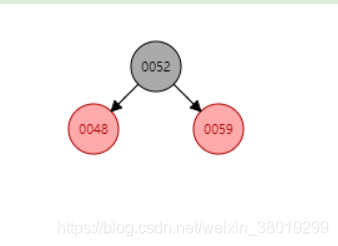
  插入52后，以父节点48左旋，左旋后，52和59互换颜色，再以59为结点右旋即可。

3.1.3 父亲结点为右孩子，插入结点也为右孩子
将父亲结点和爷爷结点的颜色互换，然后针对爷爷结点进行一次左旋


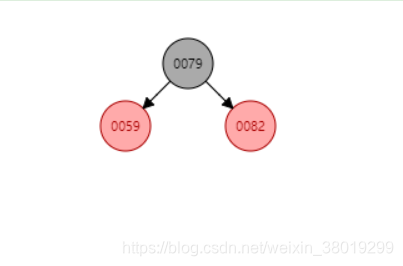
插入82后，59和79互换颜色，然后再进行左旋即可。
3.1.4 父亲结点为左孩子，插入结点也为左孩子
将父亲结点和爷爷结点的颜色互换，然后针对爷爷结点进行一次右旋
这种情况与3.1.1情况雷同。


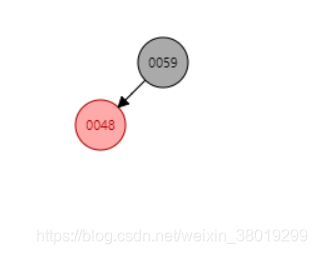
插入50以后，48和59颜色互换，然后对59进行左旋即可。
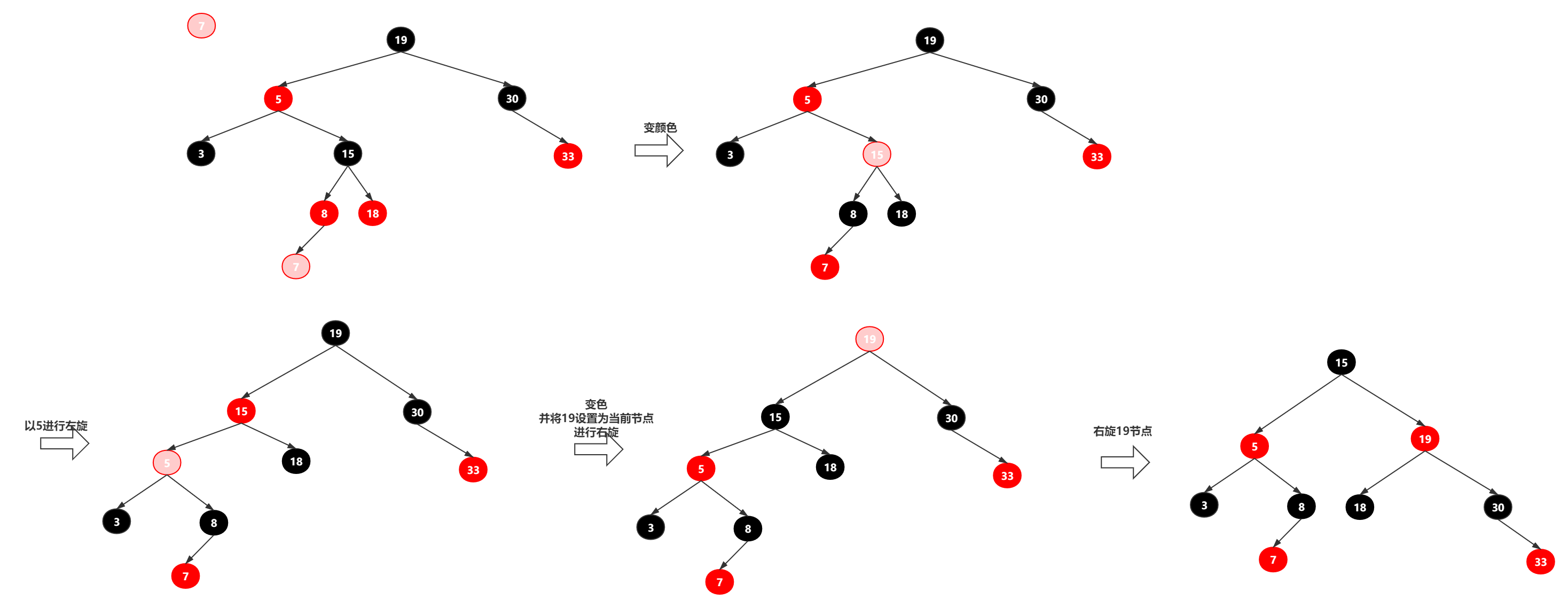
3.2 叔叔节点为红色的情况
将叔叔和父亲结点改为黑色，爷爷结点改为红色，然后又将爷爷节点当做插入点做此操作。

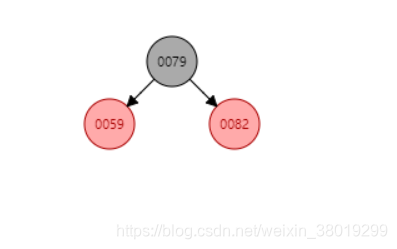
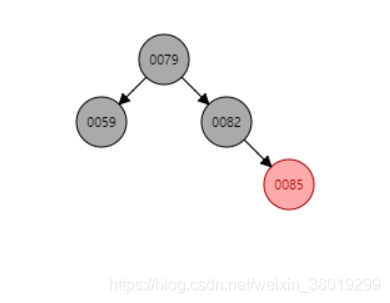
插入85后，将父亲和叔叔结点变为黑色，将爷爷节点变红，但发现爷爷节点为根节点，所以满足性质2，将根节点变为黑色即可。

• 删除
  删除同样在删除操作后要进行一些列变化使树仍然具有红黑树的性质。
  删除情况有三种：
  1.删除结点没有儿子的情况：

1）删除结点为红色
直接删除，不影响红黑树性质
2）删除结点为黑色，其兄弟结点没有儿子
将兄弟节点变成红色，将父亲节点变成黑色，保持性质5。
如图，删除96这个节点：

删除后

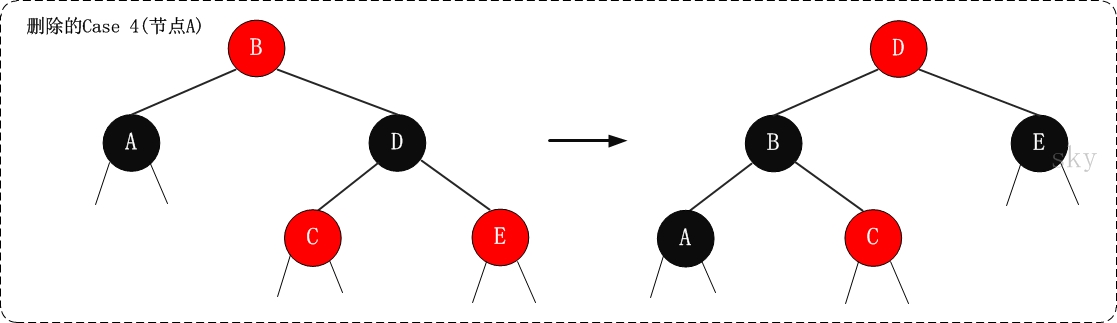
3）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子为右孩子和其父亲节点在同一边。
首先删除，当前节点83，然后把兄弟节点和父亲节点交换，在把父亲节点变黑，然后，把兄弟节点子节点变黑：
1.如果兄弟结点和兄弟结点的儿子都在右子树的话：对父亲结点进行左旋
2.如果兄弟结点和兄弟结点的儿子都在左子树的话：对父亲结点进行右旋
如图列出为第二种情况：

删除后

4）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子为左孩子
限于篇幅和时间问题，后面的各种情况就不一一作图说明了。
如果要想自己尝试，或者看这个过程请看 红黑树演示地址
5）删除结点为黑色，其兄弟结点有两个孩子，而且兄弟结点为红色
6）删除结点为黑色，其兄弟结点有两个孩子，而且兄弟结点为黑色
二.删除结点只有一个儿子的情况：
1）删除结点为黑色，其唯一的儿子结点为红色（必定是红色，要不然不符合红黑树的第5条性质）
2）删除结点为红色，其儿子结点只能为黑：红黑树中不存在这种情况，要不然无法满足红黑树第5条性质
三.删除结点有两个儿子的情况；
以上就是删除的三种情况。

总结

红黑树的情况比较复杂，但是不难理解，首先要理解平衡二叉树，对左右旋转要理解，熟悉红黑树的五个性质，不管是删除添加都要保持这5个性质同时其又是一个特殊的平衡二叉树。