红黑树简介
红黑树是一种自平衡的二叉查找树,它的统计性能要优于平衡二叉树,因此在很多地方都有应用,例如Java中的TreeMap,HashMap等数据结构都使用到了红黑树。红黑树对很多人来说熟悉而陌生,熟悉则是因为知道红黑树在很多场景中有使用,但又对其原理很陌生或者一知半解。今天就来剖析一下红黑树原理
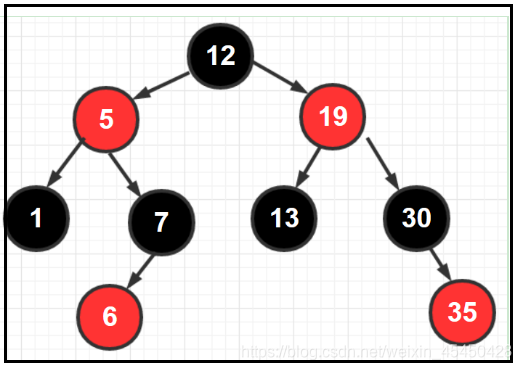
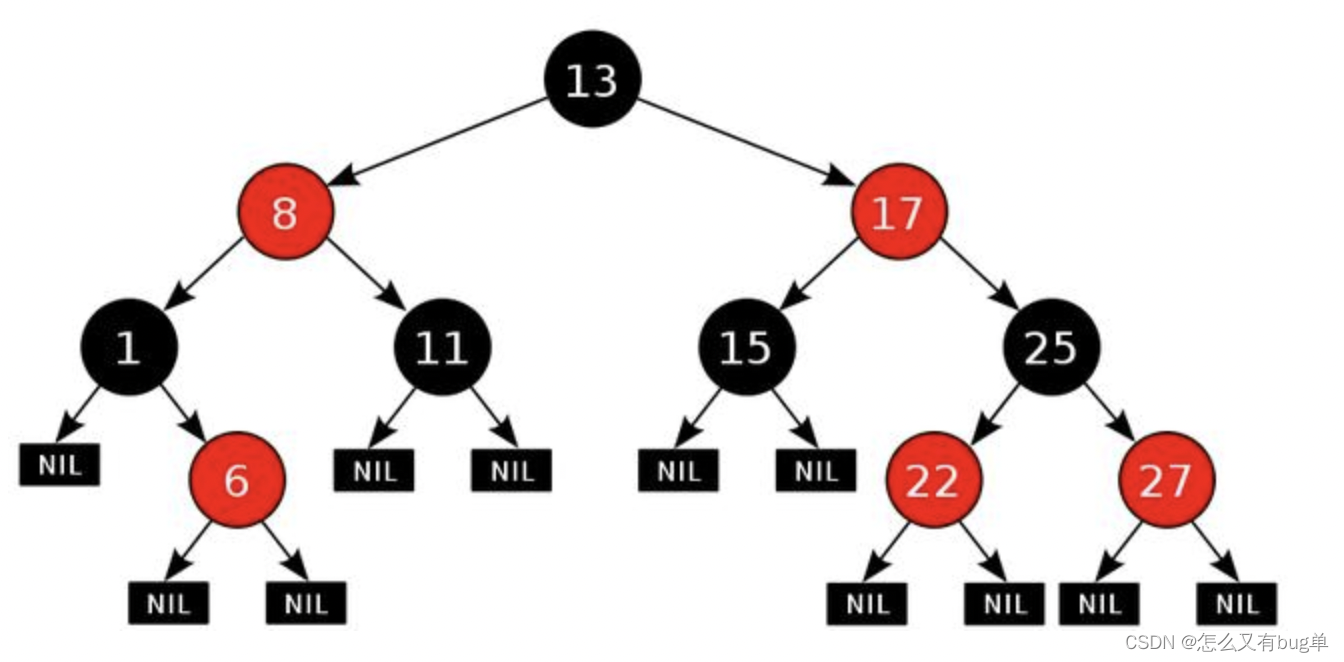
红黑树是一种二叉查找树,但是它在二叉查找树基础上增加了着色和相关的性质使得其相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。红黑树具备以下5个性质:
1.每个节点要么是黑色,要么是红色
2.根节点是黑色
3.每个叶子节点(NIL)是黑色
4.每个红色节点的子节点一定是黑色,不能有两个红色节点相连
5.任意一节点到每个叶子节点的路径包含的黑节点数量相同。俗称黑高
以上5个性质是硬性规定,记忆即可
红黑树的操作
插入节点
旋转
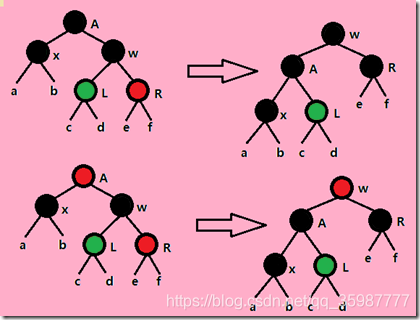
在讲插入节点之前,先普及一下树的旋转,如果学习过平衡树的程序员应该都会大概知道旋转的操作。旋转分为左旋和右旋,下面两个动图很形象的解释了左旋和右旋:
左旋:

左旋就是父节点退化成其右子节点的的左子节点,而原本的右子节点升级为父节点,一般有两个步骤:
1.当前节点E与其右子节点S的左子节点相连,作为当前节点E的右子节点
2.用当前节点E的右子节点替换E的位置,E变成S的左子节点
右旋:

右旋就是父节点退化成其左子节点的右子节点,而原本的左子节点升级为父节点,一般有两个步骤:
1.将当前节点S与其左子节点的右子节点相连,作为当前节点S的左子节点
2.用当前节点S的左子节点E替换S的位置,S变成E的右子节点
在插入新节点之前,需要明确两个共识:
1.插入新节点有可能会破坏原红黑树的平衡,因此需要对新的树进行调整变为红黑树;
2.插入的节点必须是红色,因为插入黑色节点必然会导致一条路径上黑色节点数量+1,破坏红黑树的黑色平衡
现在我们来分析一下插入节点后可能面临的几种情况:
- 如果树为空,插入新节点,需要将新增节点赋给根节点,并将节点变成黑色
- 如果新节点的父节点为黑色,则不需要进行任何平衡操作,因为新增的红色节点没有破坏红黑树的性质4,5
- 如果新节点的父节点为红色,父节点有可能是爷爷节点的左子节点和右子节点两种情况:
3.1. 父节点是爷爷节点的左子节点,有如下3中情形:
3.1.1. 叔叔节点也是红色(新节点是父节点的左还是右子节点不影响):
解决方案:将父节点和叔叔节点都变成黑色,爷爷节点变成红色,然后将爷爷节点当成新插入节点,继续同样的操作,直到当前节点变成根节点,然后将根节点变成黑色
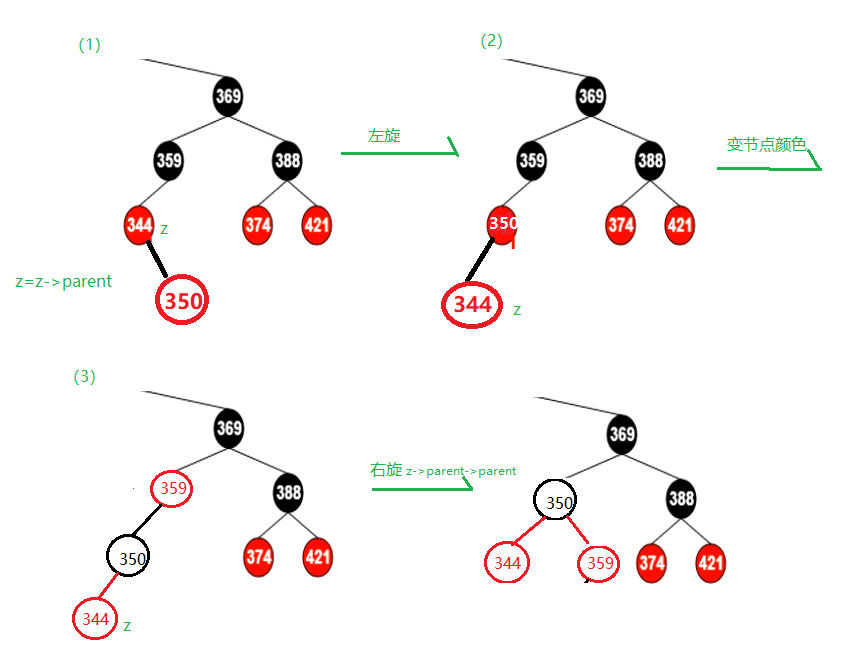
3.1.2.新增节点是父节点的左子节点,但叔叔节点是黑色(简称“左左”)
解决方案:将父节点变成黑色,爷爷节点变成红色,然后将爷爷节点右旋
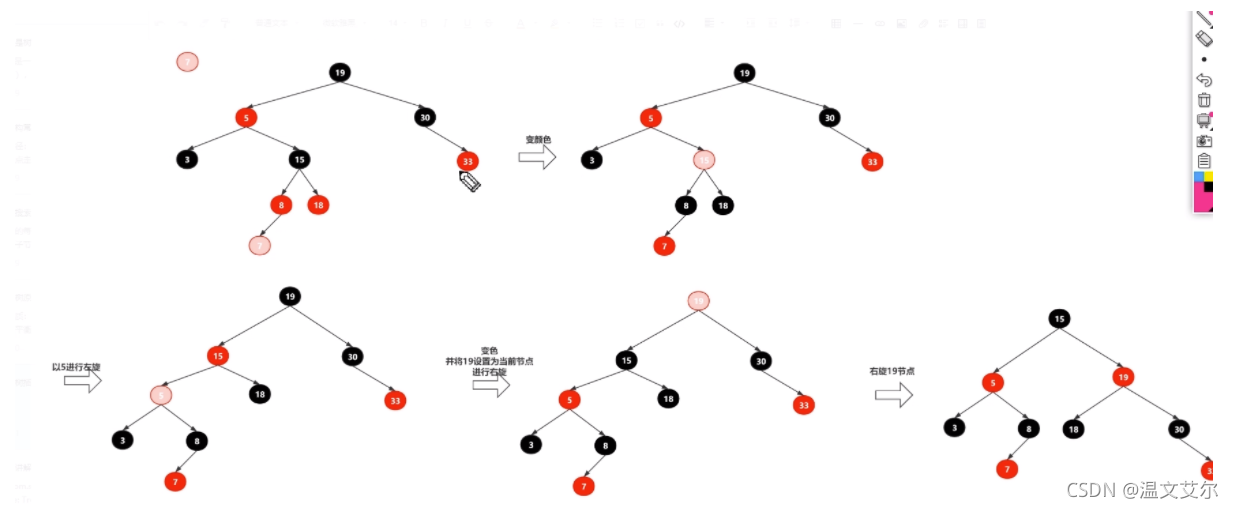
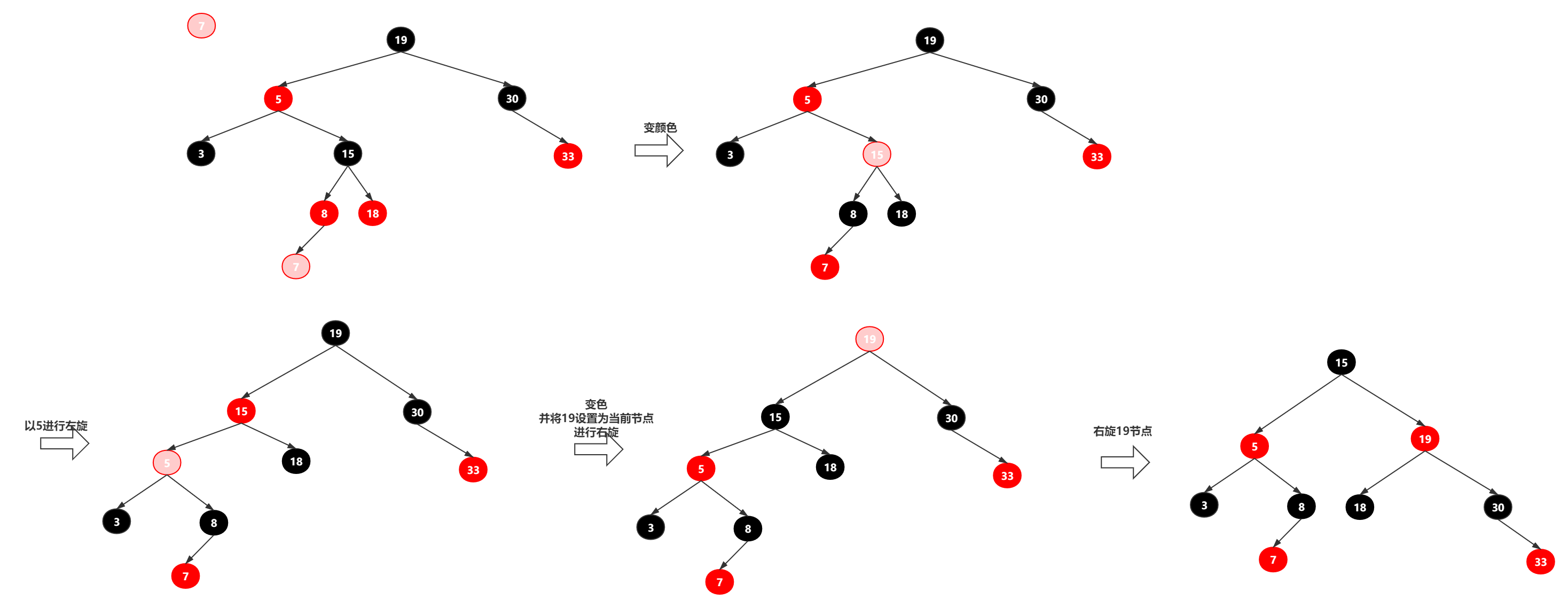
3.1.3.新增节点是父节点的右子节点,叔叔节点是黑色(简称“左右”)
解决方案:对父节点进行左旋,就变成了和3.1.2一样的树,按照3.1.2进行再处理
3.2.父节点是爷爷节点的右子节点,与上述一样也有3中情形:
3.2.1.叔叔节点是红色
解决方案与3.1.1一样
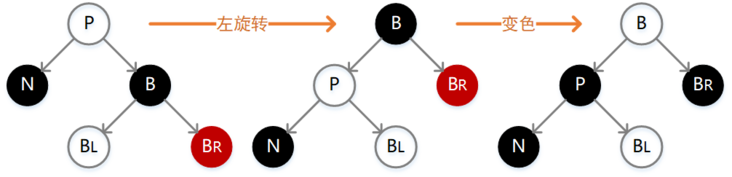
3.2.2.新增节点是父节点的右子节点,叔叔节点为黑色(简称“右右”)
解决方案:将父节点变为黑色,爷爷节点变为红色,然后将爷爷节点左旋
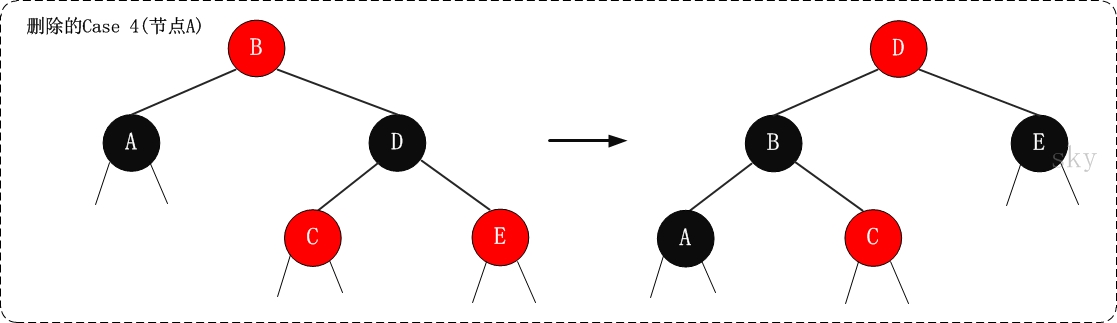
3.2.3.新增节点是父节点的左子节点,叔叔节点为黑色(简称“右左”)
解决方案:将父节点进行右旋,就变成了3.2.2一样的树,按照3.2.2进行再处理
代码处理
定义红黑树类RBTree:
public class RBTree<K extends Comparable<K>, V> {private static final boolean RED = false;private static final boolean BLACK = true;/*** 根节点引用*/private RBNode root;
}
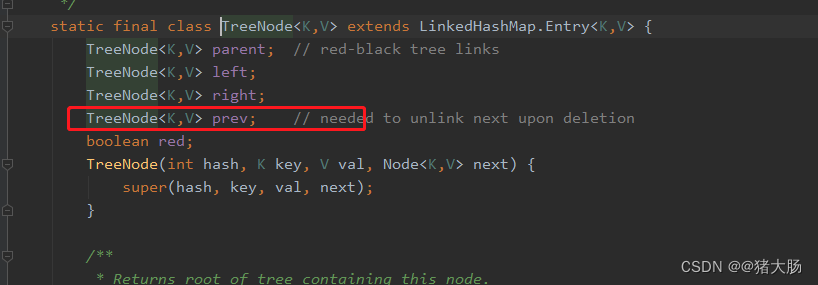
定义节点类RBNode,这里直接定义在RBTree中作为静态内部类
static class RBNode<K extends Comparable<K>, V> {K key;V value;RBNode left;RBNode right;RBNode parent;boolean color = BLACK;public void setValue(V value) {this.value = value;}public V getValue() {return value;}
}
左旋操作:
/*** 左旋* p.parent r.parent* 丨 丨* p --------> r* / \ / \* p.left r p y* / \ / \* x y p.left x* p:当前操作节点* 1.将p的右子节点更新为r的左子节点,r的左子节点的父节点更新为p* 2.r替换p的位置,即r的父节点更新为p的父节点,p的父节点的子节点更新为r* 3.r的左子节点更新为p,p的父节点更新为r* 如果当前节点为null,不操作** @param p*/
private void rotateLeft(RBNode p) {if (p != null) {RBNode r = p.right;// 1.1 将p的右子节点更新为r的左子节点p.right = r.left;// 1.2 r的左子节点的父节点更新为pif (r.left != null) {r.left.parent = p;}// 2.1 r的父节点更新为p的父节点r.parent = p.parent;// 2.2 p的父节点的子节点更新为rif (p.parent == null) {root = r;} else if (p.parent.left == p) {p.parent.left = r;} else {p.parent.right = r;}// 3 r的左子节点更新为p,p的父节点更新为rr.left = p;p.parent = r;}
}
右旋操作:
/*** 右旋* p.parent r.parent* 丨 丨* p --------> l* / \ / \* l p.right x p* / \ / \* x y y p.right* p:当前操作节点* 1.将p的左子节点更新为l的右子节点,l的右子节点的父节点更新为p* 2.l替换p的位置,即l的父节点更新为p的父节点,p的父节点更新为l* 3.l的右子节点更新为p,p的父节点更新为l* 如果当前节点为null,不操作* @param p*/
private void rotateRight(RBNode p) {if (p != null) {RBNode l = p.left;p.left = l.right;if (l.right != null) {l.right.parent = p;}l.parent = p.parent;if (p.parent == null) {root = l;} else if (p.parent.left == p) {p.parent.left = l;} else {p.parent.right = l;}l.right = p;p.parent = l;}
}
插入节点后的调整动作:
/*** 对插入新节点后的二叉树进行调整转成红黑树** @param x*/
private void fixAfterInsertion(RBNode x) {x.color = RED; // 新插入的节点必须为红色// 不需要任何调整的情况:新节点的父节点为黑色// 如果新节点就是root节点,只需变色即可// 最为简单的情况,暂不予考虑while (x != root && x.parent.color == RED) {if (x.parent == x.parent.parent.left) { // 新节点的父节点是祖父节点的左子节点RBNode y = x.parent.parent.right; // 叔叔节点if (colorOf(y) == RED) { // 叔叔节点也为红色// 将父节点和叔叔节点变为黑色,祖父节点变为红色,再把祖父节点当做新节点依次雷同操作,直到祖父节点为root或黑色setColor(x.parent, BLACK);setColor(y, BLACK);setColor(x.parent.parent, RED);x = x.parent.parent;} else { // 叔叔节点为黑色// 需要判断新节点是父节点的左子节点还是右子节点if (x == x.parent.right) { // 左右,先父节点左旋,之后与左左一致做法x = x.parent;rotateLeft(x);}// 左左setColor(x.parent, BLACK);setColor(x.parent.parent, RED);// 祖父节点右旋rotateRight(x.parent.parent);}} else { // 新节点的父节点是祖父节点的右子节点RBNode y = x.parent.parent.left;if (colorOf(y) == RED) {setColor(x.parent, BLACK);setColor(y, BLACK);setColor(x.parent.parent, RED);} else {if (x == x.parent.left) {x = x.parent;rotateRight(x);}setColor(x.parent, BLACK);setColor(x.parent.parent, RED);rotateLeft(x.parent.parent);}}}
}
插入新节点:
/*** 插入节点* @param node*/
public void insert(RBNode node) {if (node == null) {return;}if (root == null) { // 初始化rootroot = node;root.color = BLACK;return;}RBNode x = root;RBNode p = null;// p用来记录x的父节点int cmp;do {p = x;cmp = node.key.compareTo(x.key);// cmp > 0:新节点比当前节点大;cmp < 0:新节点比当前节点小;否则相等if (cmp < 0) {// 往当前结点的左子节点遍历x = x.left;} else if (cmp > 0){ // 往右子节点遍历x = x.right;} else {x.setValue(node.getValue());}} while (x != null);node.parent = p;if (cmp < 0) {p.left = node;}else {p.right = node;}// 插入新节点后,进行调整转成红黑树fixAfterInsertion(node);
}
以上只完成了红黑树新增节点的原理解释以及代码实现,删除节点操作会放在后面的文章中讲解。红黑树的源码可在JDK源码TreeMap中查看,当然如果想看有注释版的,也可以到我的github查看:https://github.com/ithushuai/tree