C++深度优先和广度优先的实现
- 前言
- 源码如下:
- 测试结果
- 深度优先(栈实现)和广度优先(队列实现)图解
前言
本篇文章为笔者的读书笔记,未经允许请勿转载。如果对你有帮助记得点个赞(●’◡’●)
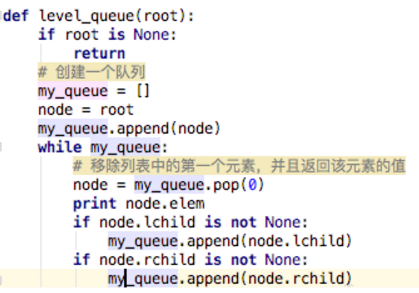
本文主要讲的深度优先算法和广度优先算法的区别,其中深度优先有两种实现方式,一种是递归法,另一种是非递归(栈实现),而广度优先就是队列的实现;
后面还会以图形表述栈实现和队列实现;且用到了图形库easyx;
源码如下:
main
#include <iostream>
#include<vector>
#include<windows.h>
#include"Draw.h"
#include"DFS.h"
#include"BFS.h"
#include"Search.h"
using namespace std;
vector<vector<int>> map =
{{0,0,1,0,1,0,1},{1,0,0,0,0,0,1},{1,0,1,1,1,0,0},{1,0,0,0,1,1,1},{0,0,1,0,0,0,1},{1,0,1,0,1,0,0},{1,0,1,1,1,0,1},
};
//检查数据的合法性
bool check(int x, int y)
{//所走的路径不能越界,也不能走到地图为1的地方。if ((y < 0 || x<0) || y >= map.size() ||x>=map[y].size() || map[y][x] == 1){return false;}return true;
}
//测试图形库是否能正常运行
void test()
{Draw draw(600, map);draw.updata();
}
//深度优先算法
void test1()
{DFS dfs(check);Draw draw(600, map);Pos start{ 0,0 };Pos end{ 1,6 };draw.level[end.y][end.x] = Draw::end;//设置终点位置draw.updata();const auto& path = dfs.recursive(start,end);//开始寻路,路径找完后用vector保存了for (const auto& e : path){draw.level[e.y][e.x] = Draw::visit;//路径设置为visit。注意x,y不要写反了draw.updata();Sleep(500);}
}
//广度优先算法
void test2()
{BFS bfs(check);Draw draw(600, map);Pos start{ 1,1 };Pos end{ 3,0 };draw.level[end.y][end.x] = Draw::end;draw.updata();const auto& path = bfs.queue(start, end);for (const auto& e : path){draw.level[e.y][e.x] = Draw::visit;draw.updata();Sleep(500);}}
int main()
{//test();//test1();//test2();system("pause");return 0;
}
Draw.h
#pragma once
#include<vector>
#include<easyx.h>
#include<string>
#include<iostream>//区别名
using vec2 = std::vector<std::vector<int>>;
//绘制地图的类
class Draw
{
public:Draw(int&& length, vec2& map) :length(length)
{this->level = map;this->size = length / level.size();initgraph(length, length, EW_SHOWCONSOLE);
}~Draw()
{closegraph();
}enum {road=0,//空地wall,//墙visit,//走过的路end,//终点};//绘制的地图。vec2 level;//游戏更新void updata()
{draw();test();
}
private:int length; //宽度和高度int size; //每个瓦片的大小//绘制地图void draw()
{BeginBatchDraw();//开始批量画图cleardevice();//把之前的先清除for (size_t i = 0; i < level.size(); i++){for (size_t j = 0; j < level[i].size(); j++){if (level[i][j] == road){setfillcolor(RGB(0xdd, 0xdd, 0xdd));//设置路的颜色}else if (level[i][j] == wall){setfillcolor(RGB(0x33, 0x33, 0xcc));}else if (level[i][j] == visit){setfillcolor(RGB(0x33, 0xcc, 0x33));}else if (level[i][j] == end){setfillcolor(RGB(0xff, 0x33, 0x33));}rect(j, i);//绘制瓦片,j代表x,i代表y。/*(0,0)----------▷ x的正方向||||▽ y的正方向图形库窗口的坐标*/} } EndBatchDraw();
} //绘制文本void test()
{system("cls");//清屏std::string str="";for (size_t i = 0; i < level.size(); i++){for (size_t j = 0; j < level[i].size(); j++){if (level[i][j] == road){str += " ";//设置路的标识符}else if (level[i][j] == wall){str += "+ ";//墙}else if (level[i][j] == visit){str += ". ";//走过的路}else if (level[i][j] == end){str += "= ";//终点}}str += '\n';}std::cout << str << std::endl;
} //绘制瓦片 void rect(int x, int y)
{fillrectangle(x * size, y * size, (x + 1) * size, (y + 1) * size);/* void fillrectangle(int left,int top,int right,int bottom); */}
};Search.h
#pragma once
#include<functional>
#include<vector>
struct Pos
{int x;int y;Pos(int x=0, int y=0) :x(x), y(y) {}
};
class Search
{
protected:using Function = std::function<bool(int, int)>;
public:Search(Function fn) :fn(fn) {}
protected://通过函数适配器调用外部规则,对数据进行判断;Function fn;//创建一个vector保存路径std::vector<Pos> path;//判断这条路是否走过bool isVisited(Pos pos){for (const auto& e : path){if (pos.x == e.x && pos.y == e.y){return true;}}return false;}//判断下次移动是否合法bool isValid(Pos pos){return fn(pos.x, pos.y) && !isVisited(pos);//fn调用外部规则check}
};
DFS.h
#pragma once
#include "Search.h"
//深度优先算法
class DFS : public Search
{
public:DFS(std::function<bool(int, int)> fn):Search(fn)//构造子类的时候,需要初始化父类。
{}/*start 起点坐标end 终点坐标*///递归法std::vector<Pos> recursive(Pos start, Pos end)
{this->end = end;path.push_back(start);_recursive(start);return path;
}//非递归法(栈实现)std::vector<Pos> stack(Pos start, Pos end)
{static Pos dir[4] = {{0,1},//y+1向下{1,0},//x+1向右{-1,0},//x-1向左{0,-1},//y-1向上};std::stack<Pos> st;st.push(start);while (!st.empty()){auto now = st.top();st.pop();for (size_t i = 0; i < 4; i++){//准备移动的路径Pos move(now.x + dir[i].x, now.y + dir[i].y);//判断是否能移动if (isValid(move)){st.push(move);path.push_back(move);//判断是否到达终点if (move.x == end.x && move.y == end.y){return path;}}}}return path;
}
private:bool is_end=false;//递归需要的标志位,默认位falsePos end; //保存终点坐标 void _recursive(Pos now)
{static Pos dir[4] = {{0,1},//y+1向下{1,0},//x+1向右{-1,0},//x-1向左{0,-1},//y-1向上};//判断是否到达终点if (now.x == end.x && now.y == end.y){is_end = true;//找到终点标志位置1return;}//循环遍历下右左上4个方向for (int i = 0; i < 4; i++){//准备移动的路径Pos move(now.x + dir[i].x, now.y + dir[i].y);//判断能否移动if (!is_end && isValid(move)){path.push_back(move);//保存走过的路径_recursive(move);}}
}
};
BFS.h
#pragma once
#include "Search.h"
class BFS :public Search
{
public:BFS(Function fn):Search(fn)
{
}std::vector<Pos> queue(Pos start, Pos end)
{static Pos dir[4] = {{0,1},//y+1向下{1,0},//x+1向右{-1,0},//x-1向左{0,-1},//y-1向上};std::queue<Pos> qu;qu.push(start);while (!qu.empty()){auto now = qu.front();qu.pop();for (size_t i = 0; i < 4; i++){Pos move(now.x + dir[i].x, now.y + dir[i].y);if (isValid(move)){qu.push(move);path.push_back(move);if (move.x == end.x && move.y == end.y){return path;}}}}return path;
}
};
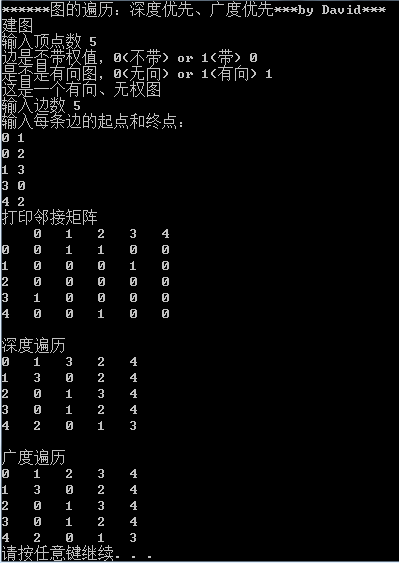
测试结果
递归实现:
深度优先(栈实现):
广度优先(队列实现)
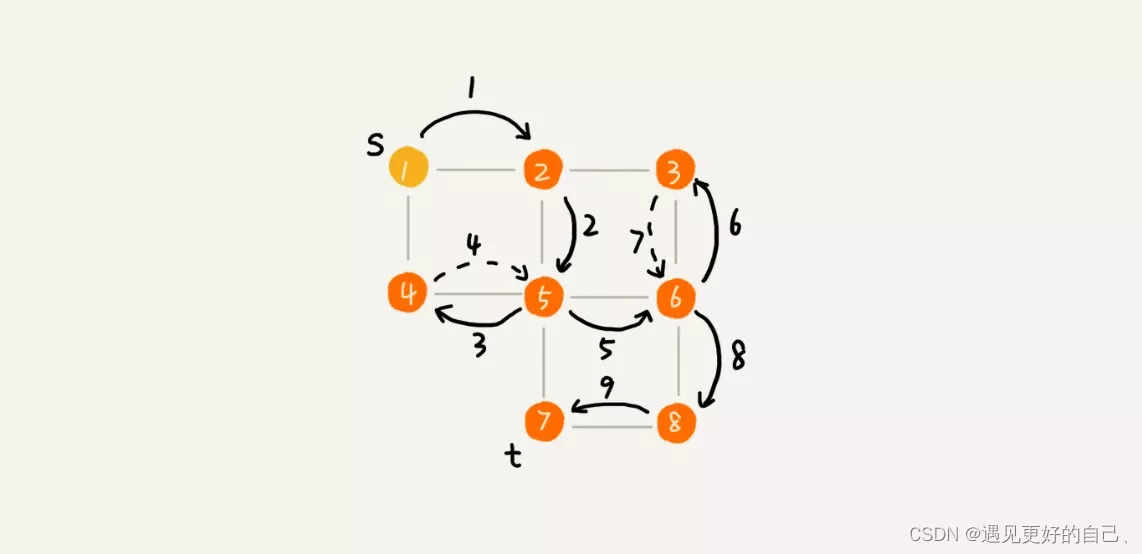
深度优先(栈实现)和广度优先(队列实现)图解
深度优先:
广度优先: