深度优先与广度优先的区别！

article/2025/9/17 4:48:15

从深度优先和广度优先两个角度解决同一个问题

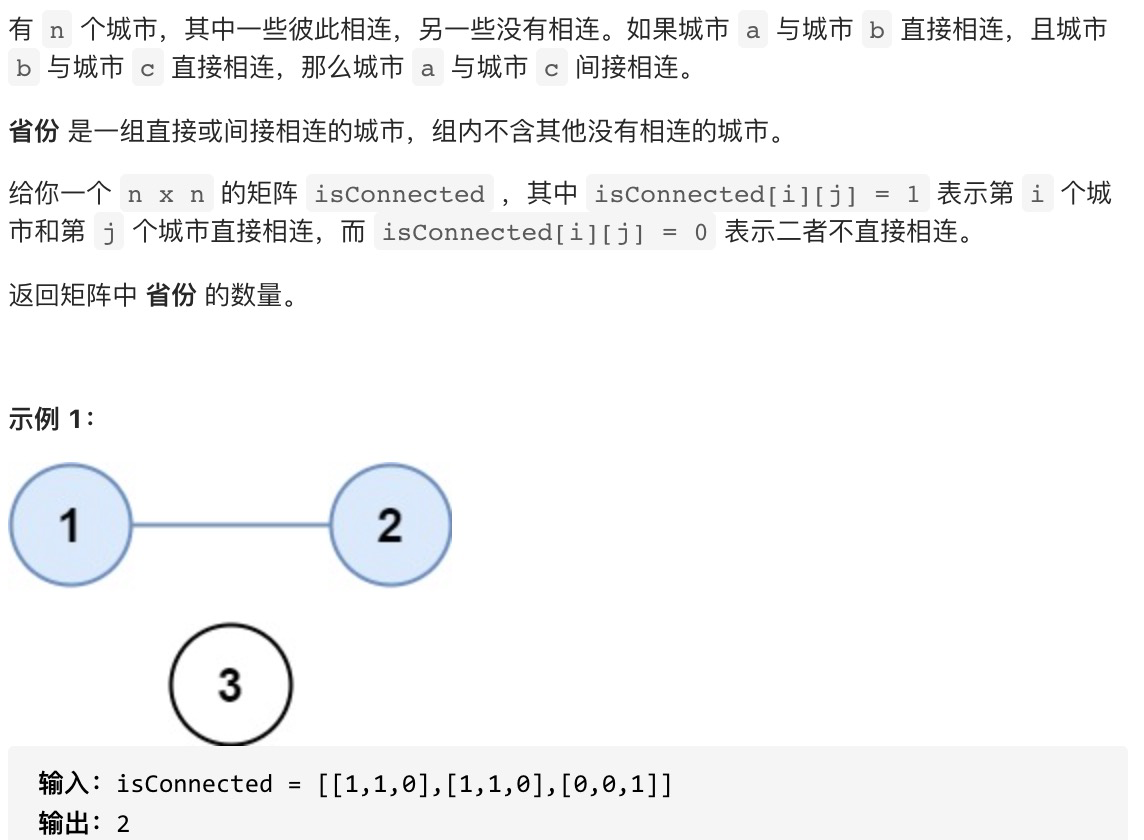
题目
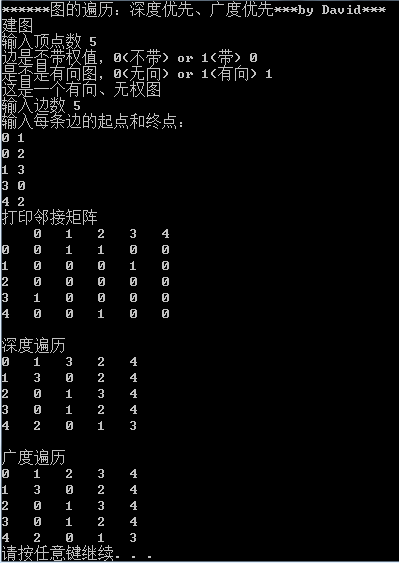
从一号顶点开始遍历这个图，使用深度优先搜索和广度优先搜索的2种遍历结果
在这里插入图片描述
深度优先遍历的主要思想就是，首先以一个未被访问过的顶点作为起始顶点，沿着当前顶点的边走到未访问过的顶点；当没有未访问过的顶点时，则回到上一个顶点，继续试探访问到末端，然后回溯，再沿着另一条进行同样的遍历，直到所有的顶点都被访问过为止。这一过程用二维数组E来存储，如下：
图的邻接矩阵法
上图二维数组中第i行第J列表示的就是顶点i到J是否有边，正无穷表示没有边，1表示有边，这里我们将自己到自己（即i等于j）设为0。我们将这种存储图的方法称为图的邻接矩阵存储法。我们发现这个二维数组是沿主对角线对称的，因为上面这个图是无向图，所谓无向图指的是图的边没有方向，例如边1-5表示1号顶点可以到5号顶点，5号顶点也可以到1号顶点。
下面上代码！

#include<stdio.h>
int book[101],sum,n,E[101][101];
void dfs(int cur)//cur是当前所在的顶点编号
{int i;printf("%d",cur);sum++;//每访问一个顶点，sum就加一if(sum==n) return ;//所有的顶点都已经访问过则直接退出for(i=1;i<=n;i++)//从1号顶点到n号顶点依次尝试，看哪些顶点与当前顶点cur有边相连{//判断当前顶点cur到顶点i是否有边，并判断顶点i是否已经访问过if(E[cur][i]==1&&book[i]==0){book[i]=1;//标记顶点i已经访问过dfs(i);//从顶点i再出发继续遍历}}return；
}
int main()
{int i,j,m,a,b;scanf("$d %d",&n,&m);//初始化二维数组for(i=1;i<=n;i++)for(j=1;j<=n;j++)if(i==j) E[i][j]=0;else E[i][j]=9999999;//我们这里假设9999999为正无穷//读入顶点之间的边for(i=1;i<=m;i++){scanf("%d %d",&a,&b);E[a][b]=1;E[b][a]=1;//这里是无向图}//从一号顶点出发book[1]=1;//标记1号顶点已访问dfs(1);//从一号顶点开始遍历getchar();getchar();return 0;
}

在上面的代码中变量cur存储的是当前正在遍历的顶点，二维数组E存储
的就是图的边（邻接矩阵），数组book用来记录哪些顶点已经访问过，变量sum用来记录已经访问过多少的顶点，变量n存储的图的顶点的总个数。
可以输入以下数据进行验证：
5 5
1 2
1 3
1 5
2 4
3 5
运行结果是：
1 2 4 3 5

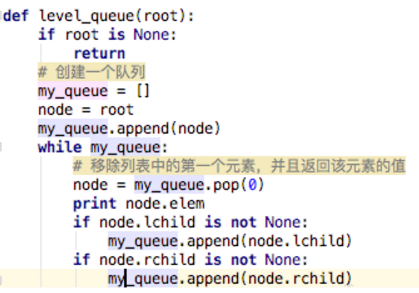
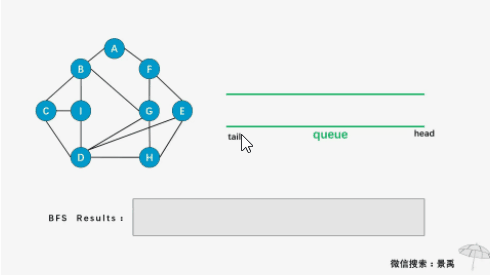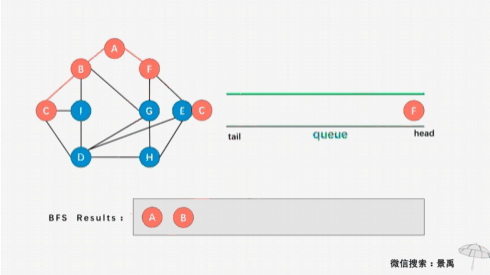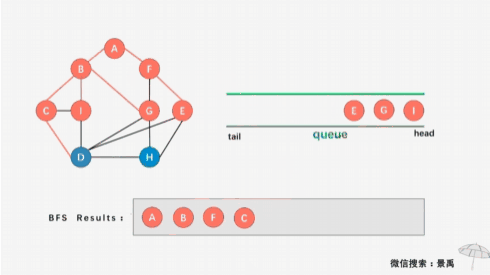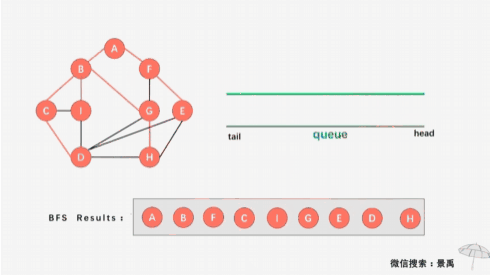
广度优先遍历的主要思想是首先以一个未被访问过的顶点作为起始点，访问其所有相邻的顶点，然后对每个相邻的顶点，再访问它们相邻的未被访问过的顶点，直到所有顶点都被访问过，遍历结束。
比如从1号顶点为起点，将1号放入队列中，然后将与1号顶点相邻的未被访问过的顶点即2号、3号和5号顶点依次再放入队列中，如下图：
在这里插入图片描述
接下来再将2号顶点相邻的未被访问过的顶点与4号顶点放入到队列中，到此所有顶点都被访问过，遍历结束。如下图：

#include<stdio.h>
int main()
{	int i,j,m,n,a,b,cur book[101]={0},E[101][101];int que[10001],head,tail;sccanf("%d %d",&n,&m);//初始化二维矩阵for (i=1;i<=n;i++)for(j=1;j<=n;j++)if(i==j) E[i][j]=0;else E[i][j]=9999999999;//读入顶点之间的边for(i=1;i<=m;i++){scanf("%d %d",&a,&b);E[a][b]=1;E[a][b]=1;}//队列初始化head=1;tail=1;//从1号顶点出发，将1号顶点加入队列que[tail]=1;tail++;book[1]=1;//标记1号顶点已访问//当队列不为空的时候循环while(head<tail&&tail<=n){cur=que[head];//当前正在访问的顶点编号for(i=1;i<=n;i++)//从1~n依次尝试{//判断从顶点cur到顶点i是否有边，并判断顶点i是否已经访问过if(E[cur][i]==1&&book[i]==0){que[tail]=i;tail++;book[i]=1；}}head++;//head++之后才能继续往下扩展}
for(i=1;i<tail;i++)printf("%d",que[i]);getchar();getchar();return 0;}