文章目录
- 1.问题简介
- 2.求解方法
- 3.深度优先搜索加回溯法
- 3.1 求解第一条可行路径
- 3.2 求解最短路径
- 4.广度优先搜索
- 小结
- 参考文献
1.问题简介
给定一个迷宫,指明起点和终点,找出从起点出发到终点的有效可行路径,就是迷宫问题(maze problem)。
迷宫可以以二维数组来存储表示。0表示通路,1表示障碍。注意这里规定移动可以从上、下、左、右四方方向移动。坐标以行和列表示,均从0开始,给定起点(0,0)和终点(4,4),迷宫表示如下:
int maze[5][5]={{0,0,0,0,0},{0,1,0,1,0},{0,1,1,0,0},{0,1,1,0,1},{0,0,0,0,0}
};
那么下面的迷宫就有两条可行的路径,分别为:
(0,0) (0,1) (0,2) (0,3) (0,4) (1,4) (2,4) (2,3) (3,3) (4,3) (4,4)(0,0) (1,0) (2,0) (3,0) (4,0) (4,1) (4,2) (4,3) (4,4) ;
可见,迷宫可行路径可能有多条,且路径长度可能不一。
2.求解方法
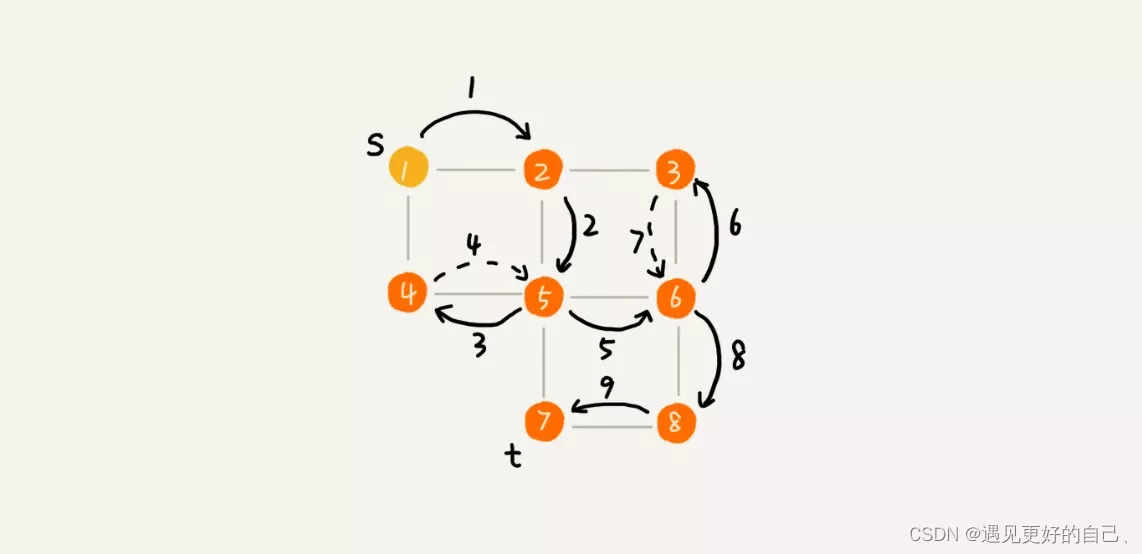
迷宫问题的求解可以抽象为连通图的遍历,因此主要有两种方法。
第一种方法:深度优先搜索(DFS)加回溯。
优点: 无需像广度优先搜索那样(BFS)记录前驱结点。
缺点: 找到的第一条可行路径不一定是最短路径,如果需要找到最短路径,那么需要找出所有可行路径后,再逐一比较,求出最短路径。
第二种方法:广度优先搜索(BFS)。
优点: 找出的第一条路径就是最短路径。
缺点: 需要记录结点的前驱结点,来形成路径。
下面将给出上面两种方法的具体步骤和实现。
3.深度优先搜索加回溯法
3.1 求解第一条可行路径
实现步骤:
(1)给定起点和终点,判断二者的合法性,如果不合法,返回;
(2)如果起点和终点合法,将起点入栈;
(3)取栈顶元素,求其邻接的未被访问的无障碍结点。求如果有,记其为已访问,并入栈。如果没有则回溯上一结点,具体做法是将当前栈顶元素出栈。其中,求邻接无障碍结点的顺序可任意,本文实现是以上、右、下、左的顺序求解。
(4)重复步骤(3),直到栈空(没有找到可行路径)或者栈顶元素等于终点(找到第一条可行路径)。
实现示例:
#include <iostream>
#include <stack>
using namespace std;struct Point{ //行与列int row; int col; Point(int x,int y){this->row=x;this->col=y;}bool operator!=(const Point& rhs){if(this->row!=rhs.row||this->col!=rhs.col)return true;return false;}
}; //func:获取相邻未被访问的节点
//para:mark:结点标记,point:结点,m:行,n:列
//ret:邻接未被访问的结点
Point getAdjacentNotVisitedNode(bool** mark,Point point,int m,int n){Point resP(-1,-1);if(point.row-1>=0&&mark[point.row-1][point.col]==false){//上节点满足条件resP.row=point.row-1;resP.col=point.col;return resP;}if(point.col+1<n&&mark[point.row][point.col+1]==false){//右节点满足条件resP.row=point.row;resP.col=point.col+1;return resP;}if(point.row+1<m&&mark[point.row+1][point.col]==false){//下节点满足条件resP.row=point.row+1;resP.col=point.col;return resP;}if(point.col-1>=0&&mark[point.row][point.col-1]==false){//左节点满足条件resP.row=point.row;resP.col=point.col-1;return resP;}return resP;
}//func:给定二维迷宫,求可行路径
//para:maze:迷宫;m:行;n:列;startP:开始结点 endP:结束结点; pointStack:栈,存放路径结点
//ret:无
void mazePath(void* maze,int m,int n,const Point& startP,Point endP,stack<Point>& pointStack){//将给定的任意列数的二维数组还原为指针数组,以支持下标操作int** maze2d=new int*[m];for(int i=0;i<m;++i){maze2d[i]=(int*)maze + i*n;}//起点和终点必须为无障碍结点,否则输入错误if(maze2d[startP.row][startP.col] == 1 || maze2d[endP.row][endP.col] == 1){return ;}//建立各个节点访问标记bool** mark=new bool*[m];for(int i=0;i<m;++i) {mark[i]=new bool[n];}for(int i=0;i<m;++i) {for(int j=0;j<n;++j){mark[i][j]=*((int*)maze+i*n+j);}}//将起点入栈pointStack.push(startP);mark[startP.row][startP.col]=true;//栈不空并且栈顶元素不为结束节点while(pointStack.empty()==false&&pointStack.top()!=endP){Point adjacentNotVisitedNode=getAdjacentNotVisitedNode(mark,pointStack.top(),m,n);if(adjacentNotVisitedNode.row==-1){ //没有未被访问的相邻节点pointStack.pop(); //回溯到上一个节点continue;}//入栈并设置访问标志为truemark[adjacentNotVisitedNode.row][adjacentNotVisitedNode.col]=true;pointStack.push(adjacentNotVisitedNode);}
}int main() {int maze[5][5]={{0,0,0,0,0},{0,1,0,1,0},{0,1,1,0,0},{0,1,1,0,1},{0,0,0,0,0}};Point startP(0,0);Point endP(4,4);stack<Point> pointStack;mazePath(maze,5,5,startP,endP,pointStack);//没有找打可行解if(pointStack.empty()==true) {cout<<"no right path"<<endl;} else {stack<Point> tmpStack;cout<<"path:";while(pointStack.empty()==false) {tmpStack.push(pointStack.top());pointStack.pop();}while (tmpStack.empty()==false) {printf("(%d,%d) ",tmpStack.top().row,tmpStack.top().col);tmpStack.pop();}}
}程序输出:
path:(0,0) (0,1) (0,2) (0,3) (0,4) (1,4) (2,4) (2,3) (3,3) (4,3) (4,4)
可见该条路径不是最短路径。因为程序中给定的迷宫还有一条更短路径为:
(0,0) (1,0) (2,0) (3,0) (4,0) (4,1) (4,2) (4,3) (4,4)
如果我们调整调用寻找下一个未访问的相邻结点的顺序,可换成先左右,后上下,可能会得到更短的路径,但无法确保在任何情况下都能得到最短路径。
3.2 求解最短路径
根据上面的方法我们可以在此基础之上进行改进,求出迷宫的最短路径。具体做法如下:
(1)让已经访问过的结点可以再次被访问,具体做法是将mark标记改为当前结点到起点的距离,作为当前结点的权值。即从起点开始出发,向四个方向查找,每走一步,把走过的点的值+1;
(2)寻找栈顶元素的下一个可访问的相邻结点,条件就是栈顶元素的权值加1必须小于下一个节点的权值(墙不能走,未被访问的结点权值为0);
(3)如果访问到终点,记录当前最短的路径。如果不是,则继续寻找下一个结点;
(4)重复步骤(2)和(3)直到栈空(迷宫中所有符合条件的结点均被访问)。
实现示例:
#include <iostream>
#include <stack>
#include <vector>
using namespace std;struct Point { //行与列int row; int col; Point(int x,int y){this->row=x;this->col=y;}bool operator!=(const Point& rhs) {if(this->row!=rhs.row||this->col!=rhs.col)return true;return false;}bool operator==(const Point& rhs) const {if(this->row==rhs.row&&this->col==rhs.col)return true;return false;}
}; //func:获取相邻未被访问的节点
//para:mark:结点标记;point:结点;m:行;n:列;endP:终点
//ret:邻接未被访问的结点
Point getAdjacentNotVisitedNode(int** mark, Point point, int m, int n, Point endP) {Point resP(-1,-1);if(point.row-1 >= 0) {//上结点满足条件if(mark[point.row-1][point.col] == 0 || mark[point.row][point.col]+1<mark[point.row-1][point.col]) {resP.row=point.row-1;resP.col=point.col;return resP;}}if(point.col+1 < n) {//右结点满足条件if(mark[point.row][point.col+1] == 0 || mark[point.row][point.col]+1<mark[point.row][point.col+1]){resP.row=point.row;resP.col=point.col+1;return resP;}}if(point.row+1 < m){//下结点满足条件if(mark[point.row+1][point.col] == 0 || mark[point.row][point.col]+1<mark[point.row+1][point.col]){resP.row=point.row+1;resP.col=point.col;return resP;}}if(point.col-1 >= 0){//左结点满足条件if(mark[point.row][point.col-1] == 0 || mark[point.row][point.col]+1<mark[point.row][point.col-1]){resP.row=point.row;resP.col=point.col-1;return resP;}}return resP;
}//func:给定二维迷宫,求可行路径
//para:maze:迷宫;m:行;n:列;startP:开始结点 endP:结束结点; pointStack:栈,存放路径结点;vecPath:存放最短路径
//ret:无
void mazePath(void* maze,int m,int n, Point& startP, Point endP,stack<Point>& pointStack,vector<Point>& vecPath)
{//将给定的任意列数的二维数组还原为指针数组,以支持下标操作int** maze2d=new int*[m];for(int i=0;i<m;++i){maze2d[i]=(int*)maze+i*n;}//输入错误if(maze2d[startP.row][startP.col] == -1 || maze2d[endP.row][endP.col] == -1){return;}//建立各个节点访问标记,表示结点到到起点的权值,也记录了起点到当前结点路径的长度int** mark=new int*[m];for(int i=0;i<m;++i){mark[i]=new int[n];}for(int i=0;i<m;++i){for(int j=0;j<n;++j){mark[i][j] = *((int*)maze+i*n+j);}}//起点等于终点if(startP==endP){vecPath.push_back(startP);return;}//增加一个终点的已被访问的前驱结点集vector<Point> visitedEndPointPreNodeVec;//将起点入栈pointStack.push(startP);mark[startP.row][startP.col] = 1;//栈不空并且栈顶元素不为结束节点while(pointStack.empty() == false){Point adjacentNotVisitedNode=getAdjacentNotVisitedNode(mark,pointStack.top(),m,n,endP);//没有符合条件的相邻结点if(adjacentNotVisitedNode.row == -1){//回溯到上一个节点,继续深度搜索pointStack.pop();continue;}//以较短的路径,找到了终点if(adjacentNotVisitedNode == endP){mark[adjacentNotVisitedNode.row][adjacentNotVisitedNode.col] = mark[pointStack.top().row][pointStack.top().col] + 1;pointStack.push(endP);stack<Point> pointStackTemp=pointStack;vecPath.clear();while (pointStackTemp.empty() == false){//vecPath 存放的是逆序路径vecPath.push_back(pointStackTemp.top());pointStackTemp.pop();}pointStack.pop(); //将终点出栈continue;}//入栈并设置结点权值mark[adjacentNotVisitedNode.row][adjacentNotVisitedNode.col]=mark[pointStack.top().row][pointStack.top().col]+1;pointStack.push(adjacentNotVisitedNode);}
}int maze[5][5]={{0, 0, 0, 0,0},{0,-1, 0,-1,0},{0,-1,-1, 0,0},{0,-1,-1, 0,-1},{0, 0, 0, 0, 0}
};int main(){Point startP(0,0);Point endP(4,4);stack<Point> pointStack;vector<Point> vecPath;mazePath(maze,5,5,startP,endP,pointStack,vecPath);if(vecPath.empty()==true){cout << "no right path" << endl;} else {cout<<"shortest path:";for(auto i=vecPath.rbegin();i!=vecPath.rend();++i){printf("(%d,%d) ",i->row,i->col);}}
}
程序输出最短路径如下:
如果将程序的迷宫改为如下:
int maze[5][3] = {
0, -1, 0,
0, -1 ,0,
1, -1, 0 ,
0, -1, 0,
0 ,0, 0};
输出:
根据改进的办法,可以看到上段代码修改的地方主要有三个地方:
(1)mark 标记改为结点权值,记录起点到结点的路径长度。特殊地,起点的权值记为 1。
(2)为适应 mark 标记,将迷宫的墙改为 -1,以免与结点权值混淆。
(3)求解下一个访问的结点,判断条件是结点的权值要小于其当前权值。
4.广度优先搜索
广度优先搜索的优点是找出的第一条路径就是最短路径,所以经常用来搜索最短路径,思路和图的广度优先遍历一样,需要借助队列。
实现步骤:
(1)从入口元素开始,判断它上下左右的邻边元素是否满足条件,如果满足条件就入队列;
(2)取队首元素并出队列。寻找其相邻未被访问的元素,将其如队列并标记元素的前驱节点为队首元素;
(3)重复步骤(2),直到队列为空(没有找到可行路径)或者找到了终点。最后从终点开始,根据节点的前驱节点找出一条最短的可行路径。
实现示例:
#include <iostream>
#include <queue>
using namespace std;struct Point {//行与列int row; int col; //默认构造函数Point(){row=col=-1;}Point(int x,int y){this->row=x;this->col=y;}bool operator==(const Point& rhs) const{if(this->row==rhs.row&&this->col==rhs.col)return true;return false;}
};int maze[5][5] = {{0,0,0,0,0},{0,1,0,1,0},{0,1,1,1,0},{0,1,0,0,1},{0,0,0,0,0}
};void mazePath(void* maze,int m,int n, Point& startP, Point endP,vector<Point>& shortestPath){int** maze2d=new int*[m];for(int i=0;i<m;++i){maze2d[i]=(int*)maze+i*n;}if(maze2d[startP.row][startP.col]==1||maze2d[startP.row][startP.col]==1) return ; //输入错误if(startP==endP){ //起点即终点shortestPath.push_back(startP);return;}//mark标记每一个节点的前驱节点,如果没有则为(-1,-1),如果有,则表示已经被访问Point** mark=new Point*[m];for(int i=0;i<m;++i){mark[i]=new Point[n];}queue<Point> queuePoint;queuePoint.push(startP);//将起点的前驱节点设置为自己mark[startP.row][startP.col]=startP;while(queuePoint.empty()==false){Point pointFront=queuePoint.front();queuePoint.pop();if(pointFront.row-1>=0 && maze2d[pointFront.row-1][pointFront.col]==0){//上节点连通if(mark[pointFront.row-1][pointFront.col]==Point()){//上节点未被访问,满足条件,如队列mark[pointFront.row-1][pointFront.col]=pointFront;queuePoint.push(Point(pointFront.row-1,pointFront.col)); //入栈if(Point(pointFront.row-1,pointFront.col)==endP){ //找到终点break;}}}if(pointFront.col+1<n && maze2d[pointFront.row][pointFront.col+1]==0){//右节点连通if(mark[pointFront.row][pointFront.col+1]==Point()){//右节点未被访问,满足条件,如队列mark[pointFront.row][pointFront.col+1]=pointFront;queuePoint.push(Point(pointFront.row,pointFront.col+1)); //入栈if(Point(pointFront.row,pointFront.col+1)==endP){ //找到终点break;}}}if(pointFront.row+1<m && maze2d[pointFront.row+1][pointFront.col]==0){//下节点连通if(mark[pointFront.row+1][pointFront.col]==Point()){//下节点未被访问,满足条件,如队列mark[pointFront.row+1][pointFront.col]=pointFront;queuePoint.push(Point(pointFront.row+1,pointFront.col)); //入栈if(Point(pointFront.row+1,pointFront.col)==endP){ //找到终点break;}}}if(pointFront.col-1>=0 && maze2d[pointFront.row][pointFront.col-1]==0){//左节点连通if(mark[pointFront.row][pointFront.col-1]==Point()){//上节点未被访问,满足条件,如队列mark[pointFront.row][pointFront.col-1]=pointFront;queuePoint.push(Point(pointFront.row,pointFront.col-1)); //入栈if(Point(pointFront.row,pointFront.col-1)==endP){ //找到终点break;}}}}if(queuePoint.empty()==false){int row=endP.row;int col=endP.col;shortestPath.push_back(endP);while(!(mark[row][col]==startP)){shortestPath.push_back(mark[row][col]);row=mark[row][col].row;col=mark[row][col].col;}shortestPath.push_back(startP);}
}int main() {Point startP(0,0);Point endP(4,4);vector<Point> vecPath;mazePath(maze,5,5,startP,endP,vecPath);if(vecPath.empty()==true)cout<<"no right path"<<endl;else{cout<<"shortest path:";for(auto i=vecPath.rbegin();i!=vecPath.rend();++i)printf("(%d,%d) ",i->row,i->col);}getchar();
}
程序输出:
代码的几点说明:
(1)BFS 求迷宫最短路径,记录每个节点的前驱节点使用了mark标记。可见,三种方法中mark标记可以根据实际需求灵活为其赋予意义;
(2)特殊的,起始节点的前驱设置为其本身。
小结
告诫。看着别人的代码去理解问题是如何求解的,对于求解算法题来说,这种方法是错误的。正确的方法是看别人的求解思路,理解如何求解后,给出自己的实现,才能够真正深刻地掌握算法题的求解。经过自己思考的才能真正成为自己的东西。不然的话,看着别人的代码痛苦不说,而且每个人的实现在很多细节上不尽相同,即使花了很长时间,暂时弄明白了,我想过不了多久就会忘记。这样,得不偿失!
参考文献
[1] 迷宫最短路径问题解析
[2] 迷宫问题