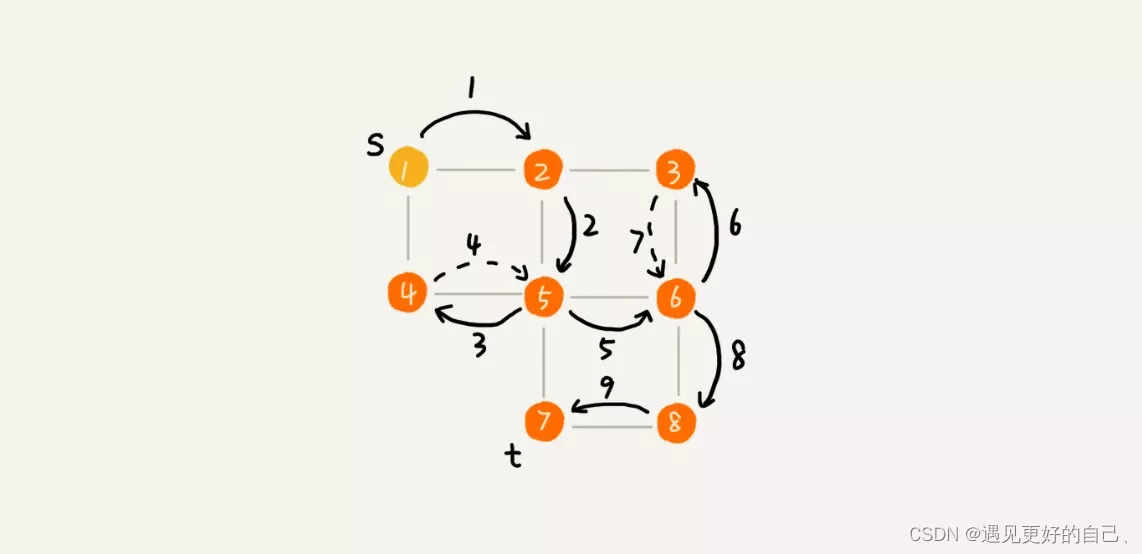
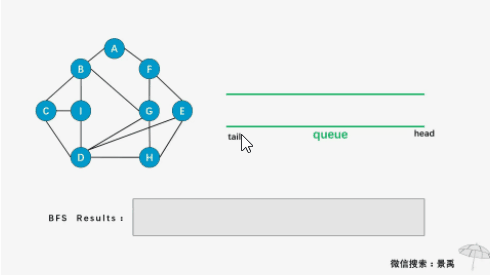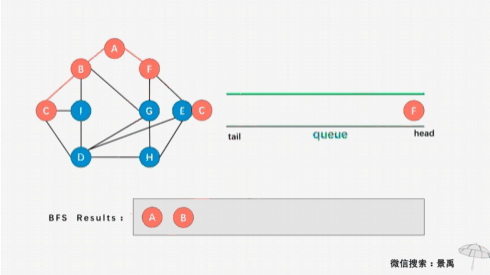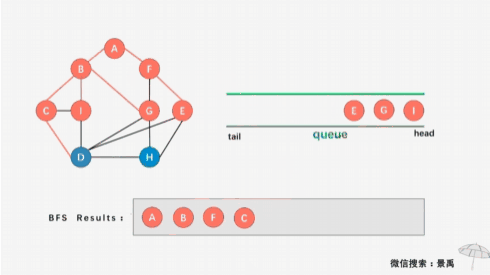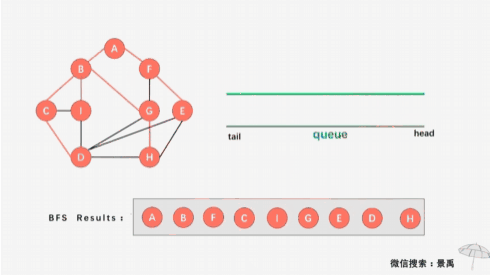
1. 编写一个程序，输出下面带权有向图的邻接表，并根据该邻接表，实现图的遍历运算，具体要求如下：
   (1)从顶点0开始的深度优先遍历序列(递归算法)
   (2)从顶点0开始的深度优先遍历序列(非递归算法)
   (3)从顶点0开始的广度优先遍历序列
   

#include <iostream>
#include<bits/stdc++.h>
#define MAXV 100
#define MaxSize 100
#define INF 327676
using namespace std;
typedef char InfoType;
typedef char ElemType;//邻接矩阵声明
typedef struct
{int no;InfoType info;
} VertexType;
typedef struct
{int edges[MAXV][MAXV];int n,e;VertexType vexs[MAXV];
} MatGraph;
//邻接表声明
typedef struct ANode
{int adjvex;struct ANode *nextarc;int weight;
} ArcNode;
typedef struct Vnode
{InfoType info;ArcNode *firstarc;
} VNode;
typedef struct
{VNode adjlist[MAXV];int n,e;
} AdjGragh;
//创建邻接矩阵
void CreatrMat(MatGraph &g,int A[MAXV][MAXV],int n,int e)
{int i,j;g.n=n;g.e=e;for(i=0; i<g.n; i++)for(j=0; j<g.e; j++)g.edges[i][j]=A[i][j];
}
//输出邻接矩阵
void DispMat(MatGraph g)
{int i,j;for(i=0; i<g.n; i++){for(j=0; j<g.e; j++){if(g.edges[i][j]!=INF)printf("%4d",g.edges[i][j]);elseprintf("%4s","∞");}cout<<endl;}
}
//邻接矩阵转换为邻接表
void MatToList(MatGraph g,AdjGragh *&G)
{int i,j;ArcNode *p;G=(AdjGragh *)malloc(sizeof(AdjGragh));for(i=0; i<g.n; i++)G->adjlist[i].firstarc=NULL;for(i=0; i<g.n; i++){for(j=g.e-1; j>=0; j--){if(g.edges[i][j]!=0&&g.edges[i][j]!=INF){p=(ArcNode *)malloc(sizeof(ArcNode));p->adjvex=j;p->weight=g.edges[i][j];p->nextarc=G->adjlist[i].firstarc;G->adjlist[i].firstarc=p;}}}G->n=g.n;G->e=g.e;
}
//输出邻接表
void DispAdj(AdjGragh *G)
{int i;ArcNode *p;for(i=0; i<G->n; i++){p=G->adjlist[i].firstarc;printf("%3d: ",i);while(p!=NULL){printf("%3d(%d) ",p->adjvex,p->weight);p=p->nextarc;}cout<<endl;}
}
//邻接表转换成邻接矩阵
void ListToMat(AdjGragh *G,MatGraph &g)
{int i;ArcNode *p;for(i=0; i<G->n; i++){p=G->adjlist[i].firstarc;while(p!=NULL){g.edges[i][p->adjvex]=p->weight;p=p->nextarc;}}g.n=G->n;g.e=G->e;
}
//DFS递归算法
int visited[MAXV]= {0};
void DFS(AdjGragh *G,int v)
{ArcNode *p;visited[v]=1;printf("%2d",v);p=G->adjlist[v].firstarc;while(p!=NULL){if(visited[p->adjvex]==0)DFS(G,p->adjvex);p=p->nextarc;}
}
//DFS(非递归算法)
void DFS1(AdjGragh *G,int v)
{ArcNode *p;ArcNode *St[MAXV];int visited[MAXV];int top=-1,w,i;for (i=0; i<G->n; i++)visited[i]=0;printf("%2d",v);visited[v]=1;top++;St[top]=G->adjlist[v].firstarc;while (top>-1){p=St[top];top--;while (p!=NULL){w=p->adjvex;if (visited[w]==0){printf("%2d",w);visited[w]=1;top++;St[top]=G->adjlist[w].firstarc;break;}p=p->nextarc;}}
}
//队列算法
//队列定义
typedef struct
{ElemType data[MaxSize];int front,rear;
} SqQueue;
//初始化
void InitQueue(SqQueue *&q)
{q=(SqQueue *)malloc(sizeof(SqQueue));q->front=q->rear=-1;
}
//判断是否为空
bool QueueEmpty(SqQueue *q)
{return(q->front==q->rear);
}
//进队列
bool enQueue(SqQueue *&q,int e)
{if(q->rear==MaxSize-1)return false;q->rear++;q->data[q->rear]=e;return true;
}
//出队列
bool deQueue(SqQueue *&q,int &e)
{if(q->front==q->rear)return false;q->front++;e=q->data[q->front];return true;
}
//BFS非递归算法
void BFS(AdjGragh *G,int v)
{int w,i;ArcNode *p;SqQueue *qu;InitQueue(qu);int visited[MAXV];for(i=0; i<G->n; i++)visited[i]=0;printf("%2d",v);visited[v]=1;enQueue(qu,v);while(!QueueEmpty(qu)){deQueue(qu,w);p=G->adjlist[w].firstarc;while(p!=NULL){if(visited[p->adjvex]==0){printf("%2d",p->adjvex);visited[p->adjvex]=1;enQueue(qu,p->adjvex);}p=p->nextarc;}}
}//主函数
int main()
{MatGraph g;AdjGragh *G;int A[MAXV][MAXV]= {{0,5,INF,7,INF,INF},{INF,0,4,INF,INF,INF},{8,INF,0,INF,INF,9},{INF,INF,5,0,INF,6},{INF,INF,INF,5,0,INF},{3,INF,INF,INF,1,0}};printf("有向图G的邻接矩阵：\n");CreatrMat(g,A,6,6);DispMat(g);printf("图G的邻接矩阵转换成邻接表：\n");MatToList(g,G);DispAdj(G);printf("图G的邻接表转换成邻接矩阵：\n");ListToMat(G,g);DispMat(g);printf("图G的邻接表：\n");MatToList(g,G);DispAdj(G);printf("从顶点0开始的DFS（递归算法）：\n");DFS(G,0);cout<<endl;printf("从顶点0开始的DFS（非递归算法）：\n");DFS1(G,0);cout<<endl;printf("从顶点0开始的BFS（非递归算法）：\n");BFS(G,0);cout<<endl;return 0;
}