一丶深度优先（DFS）

深度优先顾名思义: 就是往深的地方优先查找或遍历。 如图二叉树，想遍历树中所有结点可以用中序遍历，前序或后序。如果某一结点还有子结点就会往深处就是往下一结点，一直遍历直到最后一个结点没有子结点时，然后退回上一级向另一个方向继续走。以前序遍历为例: 根-->左-->右  从D开始走，发现D左边还有B就继续走走到B（因为先判断作左边往左一直走下去，右边的E先不会走），到了B发现B左边有A还继续走到A，到A时发现A左没结点了再判断右边也没结点就是到头了，这时就得返回到上一级B然后向B右边的C走，以此类推一直下去就能遍历走完整棵二插树，这就是典型的深度优先应用场景。

二丶广度优先(BFS)

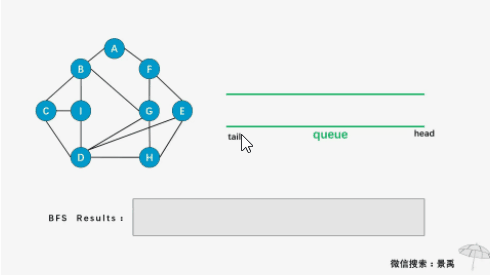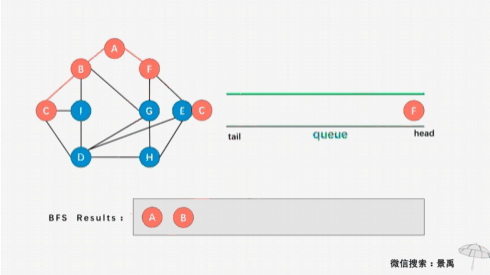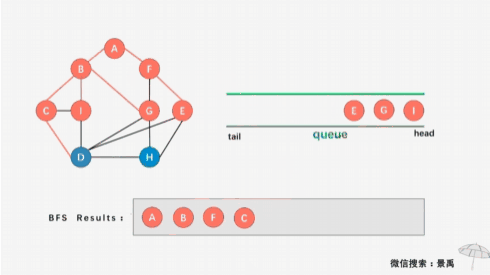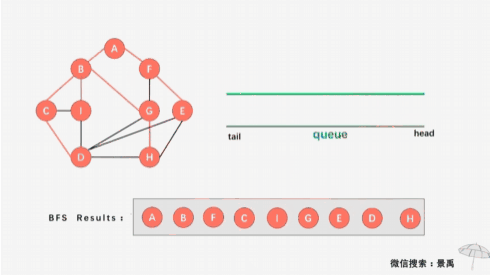
广度优先(又叫宽度优先)顾名思义：往广的地方优先查找或遍历。以上面树为例，从D开始走，发现D左边有B，如果是深度优先的话就不马上判断D的右边是否还有结点而是直接向深处就是向左直接走向B了，但是广度优先就不一样，广度优先会马上判断D是否还有其他结点比如D右边还有E，广度优先会走向B，然后E，之后以B像之前的D一样来判断怎么走，B完了又返回到E继续判断，以此类推。总之广度优先是按一层一层的来遍历: 第一层有D，第二层有B和E，第三层有A，C, G。遍历走完同一层的结点再走向下一层。

深度优先可以解决图这种数据结构的路径问题，如下图。

 图中一个结点可能会被多个其他结点指向，如果求最短路径问题这时采用广度优先遍历可以很好解决这个难题。例如广州到深圳最短距离,采用广度优先广州分别走向佛山，珠海，镍庆，再依次从佛山...等地走向深圳把所有路线比较久可以计算出最短的广州到深圳距离。