连通图里的深度优先和广度优先遍历

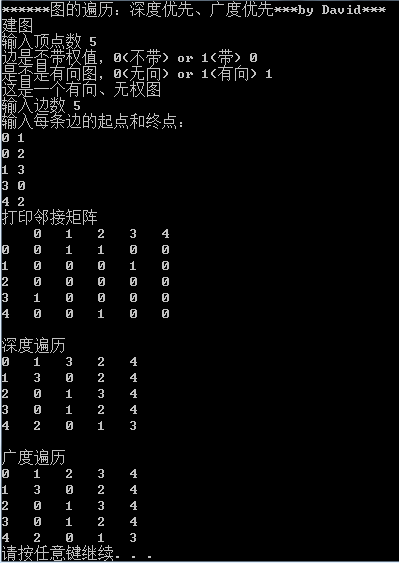
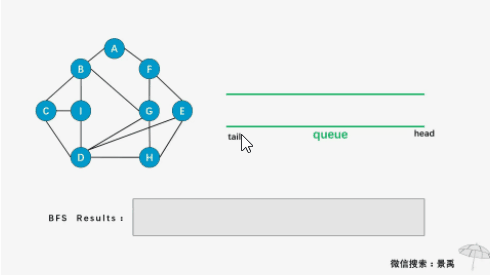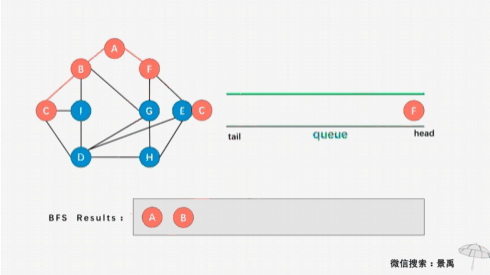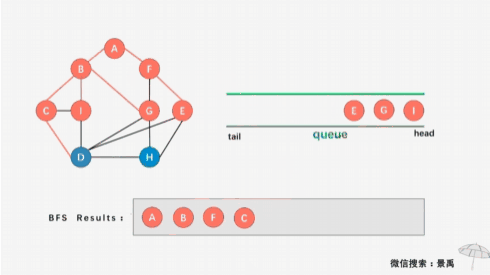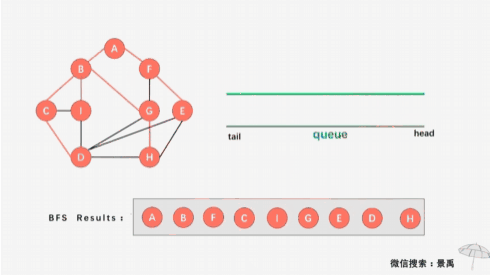
从图中的某个顶点出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使得每个顶点仅被访问一次，这个过程称为图的遍历。图的遍历有两种：深度优先遍历和广度优先遍历。
　　图分为连通图和非连通图，这里主要讨论连通图的深度、广度优先遍历。
　　一、深度优先遍历
　　图的深度优先遍历类似于树的先序遍历，它的基本思想是：首先访问指定的起始顶点 $v$ , 然后选取与 $v$ 邻接的未被访问的任意一个顶点 $w$ , 访问之，再选取与 $w$ 邻接的未被访问的任一顶点，访问之。
　　重复进行如上的访问，当一个顶点所有邻接顶点都被访问过时，则依次退回到最近被访问过的顶点，若它还有邻接顶点未被访问过，则从这些未被访问的顶点中取出一个顶点开始访问，直到所有的顶点都被访问过为止。
　　以邻接表为存储结构的深度优先遍历算法如下（其中， $v$ 是初始顶点编号，visited[]是一个全局数组，初始时所有元素均为1）：

int visited[MAXV];
//连通图的深度优先遍历
void DFS(ALGraph *G,int v){ //G指向某个邻接表，v是起始顶点ArcNode *p;visited[v]=1;                         //已访问，则置1printf("%3d",v);					  //输出被访问顶点的编号p=G->adjlist[v].firstarc;             //p指向顶点v的第一条弧的弧头结点while (p!=NULL)                     {if(visited[p->adjvex]==0)        //若p->adjvex顶点未访问，递归访问它DFS(G,p->adjvex);p=p->nextarc;                   //p指向顶点v的下一条弧的弧头结点}}

二、广度优先遍历
　　图的广度优先遍历(又叫宽度优先遍历)类似于树的层次遍历，它的基本思想是：首先访问指定的起始顶点 $v$ , 然后选取与 $v$ 邻接的全部顶点 $w_1,w_2, \cdots w_t$ , 再依次访问与 $w_1,w_2, \cdots w_t$ 邻接的全部顶点(已被访问的顶点除外)，再从这些被访问的顶点出发，逐次访问与它们邻接的全部顶点（已被访问的顶点除外）。依此类推，直到所有的顶点都被访问过为止。
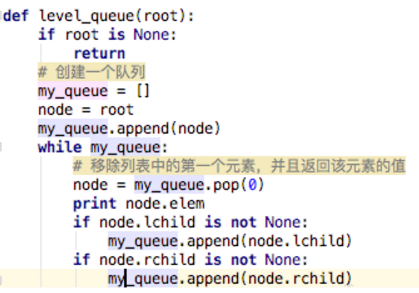
　　以邻接表为存储结构，用广度优先搜索遍历图时，需要使用一个队列，对应的算法如下：

//连通图的广度优先遍历
void BFS(ALGraph *G,int v){ //G指向某个邻接表,v是起始顶点ArcNode *p;int queue[MAXV],front=0,rear=0;      //定义循环队列并初始化int visited[MAXV];                   //定义存放结点的访问标志的数组int w,i;for(i=0;i< G->n;i++) visited[i]=0;   //访问标志数组初始化printf("%3d",v);                     //输出被访问顶点的编号visited[v]=1;                        //置已访问标记rear=(rear+1)%MAXV;queue[rear]=v;                      //v进队while (front!=rear)                 //若队列不空时循环{front=(front+1)%MAXV;w=queue[front];                //出队并赋给wp=G->adjlist[w].firstarc;      //找与顶点w邻接的第一个顶点while (p!=NULL){if (visited[p->adjvex]==0)  //若当前邻接顶点未访问{printf("%3d",p->adjvex); //访问相邻顶点visited[p->adjvex]=1;    //置该顶点已被访问的标志rear=(rear+1)%MAXV;      //该顶点进队queue[rear]=p->adjvex;}p=p->nextarc;             //找下一个邻接顶点}}printf("\n");
}

完整代码如下：

//GraphBase.h
typedef int InfoType;
#define MAXV 100       //最大顶点个数//定义邻接矩阵类型
typedef struct{int no;          //顶点编号InfoType info;   //顶点其他信息
}VertexType;       //顶点类型typedef struct{            //图的定义int edges[MAXV][MAXV]; //邻接矩阵int vexnum,arcnum;     //顶点数，弧数VertexType vexs[MAXV]; //存放顶点信息
}MGraph;                   //图的邻接矩阵类型//定义邻接表类型
typedef struct ANode{         //弧的结点结构类型int adjvex;               //该弧的终点位置 struct ANode *nextarc;     //指向下一条弧的指针InfoType info;             //弧的相关信息,用来存放权值
}ArcNode;
typedef int Vertex;
typedef struct Vnode{      //邻接表头结点的类型Vertex data;           //顶点信息ArcNode *firstarc;     //指向第一条弧
}VNode;
typedef VNode AdjList[MAXV]; //AdjList是邻接表类型
typedef struct{AdjList adjlist;     //邻接表int n,e;             //图中顶点数n和边数
}ALGraph;                //图的邻接表类型//主函数.cpp
#include <stdio.h>
#include <malloc.h>
#include "GraphBase.h"
#define INF 32767      //INF表示无穷大,即∞//将邻接矩阵g转换邻接表G
void MatToList(MGraph g,ALGraph *&G){int i,j,n=g.vexnum;                //n为顶点数ArcNode *p;G=(ALGraph *)malloc(sizeof(ALGraph));  for(i=0;i<n;i++)                       //给邻接表中所有头结点的指针域置初值G->adjlist[i].firstarc=NULL;for (i=0;i<n;i++)                    //检查邻接矩阵中的每个元素for (j=n-1;j>=0;j--)if (g.edges[i][j]!=0)        //邻接矩阵的当前元素不为0{p=(ArcNode *)malloc(sizeof(ArcNode));  //创建一个结点*pp->adjvex=j;p->info=g.edges[i][j];p->nextarc=G->adjlist[i].firstarc;   //将*p链接到链表后面G->adjlist[i].firstarc=p;}G->n=n; G->e=g.arcnum;
}//将邻接表G转换为邻接矩阵g
void ListToMat(ALGraph *G,MGraph &g){int i,j,n=G->n;ArcNode *p;for(i=0;i<n;i++)          //g.edges[i][j]赋初值0for(j=0;j<n;j++)g.edges[i][j]=0;for (i=0;i<n;i++){p=G->adjlist[i].firstarc;while(p!=NULL){g.edges[i][p->adjvex]=p->info;p=p->nextarc;}			}g.vexnum=n; g.arcnum=G->e;}//输出邻接矩阵g
void DispMat(MGraph g){int i,j;for (i=0;i<g.vexnum;i++){for(j=0;j<g.vexnum;j++)if(g.edges[i][j]==INF)printf("%3s","∞");elseprintf("%3d",g.edges[i][j]);printf("\n");}}//输出邻接表G
void DispAdj(ALGraph *G){int i;ArcNode *p;for (i=0;i< G->n;i++){p=G->adjlist[i].firstarc;if(p!=NULL) printf("%3d: ",i);while (p!=NULL){printf("%3d",p->adjvex);p=p->nextarc;}printf("\n");}}int visited[MAXV];
//连通图的深度优先遍历
void DFS(ALGraph *G,int v){ //G指向某个邻接表，v是起始顶点ArcNode *p;visited[v]=1;                         //已访问，则置1printf("%3d",v);					  //输出被访问顶点的编号p=G->adjlist[v].firstarc;             //p指向顶点v的第一条弧的弧头结点while (p!=NULL)                     {if(visited[p->adjvex]==0)        //若p->adjvex顶点未访问，递归访问它DFS(G,p->adjvex);p=p->nextarc;                   //p指向顶点v的下一条弧的弧头结点}}//连通图的深度优先遍历(非递归)
void DFS1(ALGraph *G,int v){ArcNode *p;ArcNode *St[MAXV];int top=-1,w,i;for(i=0;i< G->n;i++)visited[i]=0;printf("%3d",v);visited[v]=1;top++;St[top]=G->adjlist[v].firstarc;while (top > -1){	p=St[top]; top--;while (p!=NULL){w=p->adjvex;if (visited[w]==0){printf("%3d",w);visited[w]=1;top++;St[top]=G->adjlist[w].firstarc;break;}p=p->nextarc;}}printf("\n");
}//连通图的广度优先遍历
void BFS(ALGraph *G,int v){ //G指向某个邻接表,v是起始顶点ArcNode *p;int queue[MAXV],front=0,rear=0;      //定义循环队列并初始化int visited[MAXV];                   //定义存放结点的访问标志的数组int w,i;for(i=0;i< G->n;i++) visited[i]=0;   //访问标志数组初始化printf("%3d",v);                     //输出被访问顶点的编号visited[v]=1;                        //置已访问标记rear=(rear+1)%MAXV;queue[rear]=v;                      //v进队while (front!=rear)                 //若队列不空时循环{front=(front+1)%MAXV;w=queue[front];                //出队并赋给wp=G->adjlist[w].firstarc;      //找与顶点w邻接的第一个顶点while (p!=NULL){if (visited[p->adjvex]==0)  //若当前邻接顶点未访问{printf("%3d",p->adjvex); //访问相邻顶点visited[p->adjvex]=1;    //置该顶点已被访问的标志rear=(rear+1)%MAXV;      //该顶点进队queue[rear]=p->adjvex;}p=p->nextarc;             //找下一个邻接顶点}}printf("\n");
}void main()
{int i,j;MGraph g;ALGraph *G;int A[6][6]={{0,5,0,5,5,0},{0,0,4,0,4,0},{0,0,0,0,0,9},{0,0,0,0,0,0},{0,0,5,7,0,7},{0,0,0,0,0,0}};g.vexnum=6; g.arcnum=10;for (i=0;i<g.vexnum;i++)for(j=0;j<g.vexnum;j++)g.edges[i][j]=A[i][j];printf("\n");printf(" 有向图G的邻接矩阵: \n");DispMat(g);G=(ALGraph *)malloc(sizeof(ALGraph));printf(" 图G的邻接矩阵转换为邻接表: \n");MatToList(g,G);DispAdj(G);// 	printf(" 图G的邻接表转换为邻接矩阵: \n");
// 	ListToMat(G,g1);
// 	DispMat(g1);
// 	printf("\n");printf("深度优先遍历：\n");DFS(G,0);printf("\n");printf("深度优先遍历：\n");BFS(G,0);printf("\n");}