C语言基于邻接表的图的深度优先、广度优先遍历

article/2025/9/17 4:07:24

目录

1 深度优先（Depth_First Search）

2 广度优先（Broadth_First Search）

3 基于邻接表的深度优先、广度优先遍历

4 源代码示例

4.1 深度优先

4.2广度优先

_{}假设有无向图G = （V，E），标志数组visited [ n ]

(1)点集 V = { v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{6}, v_{7}, v_{8} }

     边集 E = {  \left (v_{1}, v_{2}\right ), \left (v_{1}, v_{3}\right ), \left (v_{2}, v_{4}\right ), \left (v_{2}, v_{5}\right ), \left (v_{3}, v_{6}\right ), \left (v_{3}, v_{7}\right ), \left (v_{4}, v_{8}\right ), \left (v_{5}, v_{8}\right ), \left (v_{6}, v_{7}\right ) }

(2)visited [ n ] (n为图中顶点个数，初始元素都为0）

若相应节点被访问过，则visited [ i ] 为 1；否则visited [ i ] 为 0

1 深度优先（Depth_First Search）

选定一个节点并遍历后，遍历该节点的第一个未被遍历邻接点；从刚遍历的节点开始，遍历该节点第一个未被遍历邻接点；

如此重复（深度含义由此可知）。若顶点的所有邻接点都被遍历，则检测visited[]数组，从元素值为0的节点开始遍历。

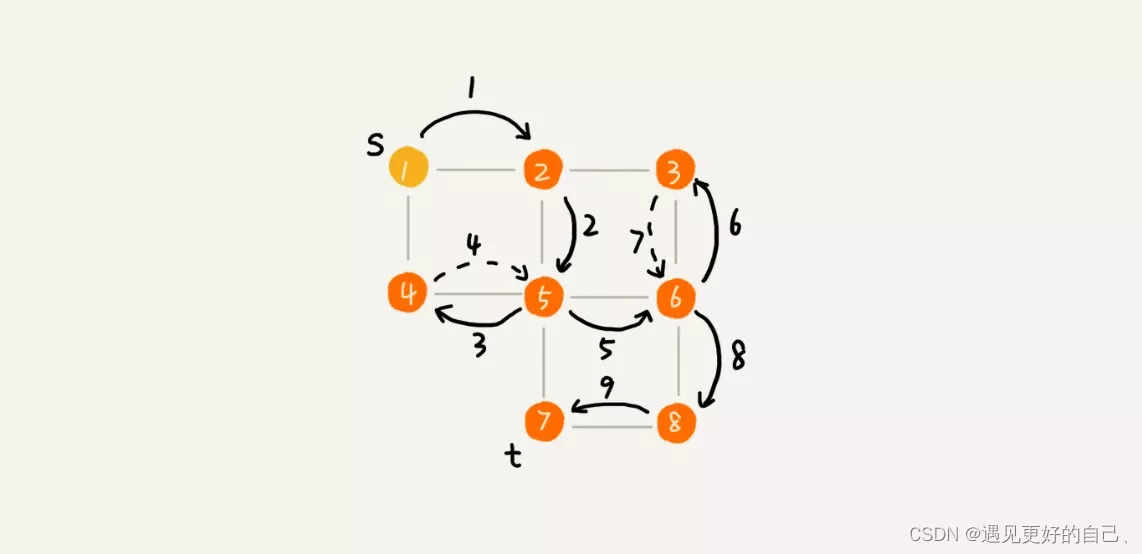
以上图为例：

从顶点V1开始遍历，然后遍历V1的第一个未被遍历邻接点V2；

从V2开始，遍历V2的第一个未被遍历邻接点V4；

从V4开始，遍历V4的第一个未被遍历邻接点V8；

从V8开始，遍历V8的第一个未被遍历邻接点V5；

从V5开始，发现V5所有邻接点都被遍历，则检测visited[]数组，发现数组中第一个未被遍历邻接点V3；

从V3开始，遍历V3的第一个未被遍历邻接点V6；

从V6开始，遍历V6的第一个未被遍历邻接点V7；

结束。

综上，深度优先序列：1,2,4,8,5,3,6,7。

2 广度优先（Broadth_First Search）

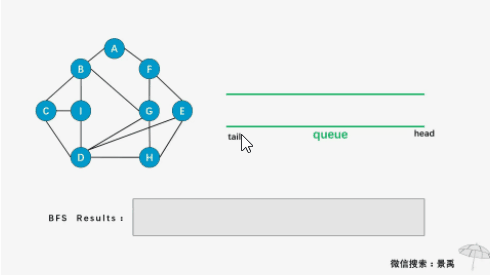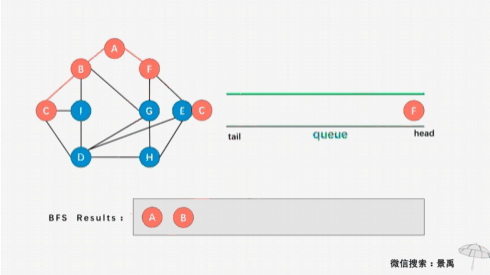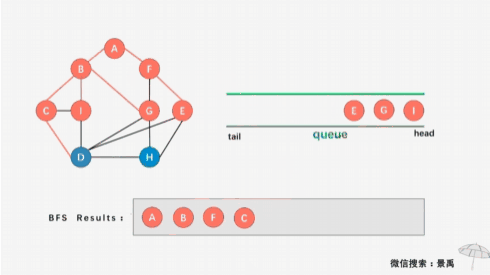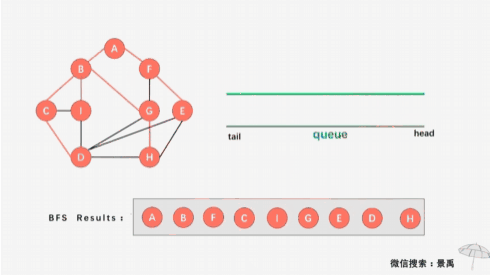
假设从顶点V1开始遍历，则遍历完V1的所有未被遍历邻接点，然后从所有邻接点中挑选出（按顺序从小到大）下标第一小的节点，再遍历该节点所有未被遍历邻接点；第二小……；第三小……。如此循环（广度含义由此可知）。若顶点的所有邻接点都被遍历，则检测visited[]数组，从元素值为0（未遍历）的节点开始遍历。

以上图为例：

从顶点V1开始遍历，然后遍历V1的所有未被遍历邻接点V2，V3；

从V2开始，遍历V2所有未被遍历邻接点V4，V5；

从V3开始，遍历V3所有未被遍历邻接点V6，V7；

从V4开始，遍历V4所有未被遍历邻接点V8。结束

综上，广度优先序列：1,2,3,4,5,6,7,8。

3 基于邻接表的深度优先、广度优先遍历

关于图的邻接表存储，可参考我的博客C语言图的邻接表存储

以上图为例，其邻接表结构如下所示：

顶点 1 ：[ 2 ] -> [ 3 ] -> NULL
顶点 2 ：[ 1 ] -> [ 4 ] -> [ 5 ] -> NULL
顶点 3 ：[ 1 ] -> [ 6 ] -> [ 7 ] -> NULL
顶点 4 ：[ 2 ] -> [ 8 ] -> NULL
顶点 5 ：[ 2 ] -> [ 8 ] -> NULL
顶点 6 ：[ 3 ] -> [ 7 ] -> NULL
顶点 7 ：[ 3 ] -> [ 6 ] -> NULL
顶点 8 ：[ 4 ] -> [ 5 ] -> NULL

深度遍历

对所有节点（1、2……8），假设从1开始访问，每访问一个节点，便将其标志数组（visited）对应位置置1，然后访问其第一个未被访问的邻接点，接着对当前访问的顶点执行同样操作。若所有邻接点都被访问，则遍历标志数组，找到第一个未被访问的节点开始访问。

如上表：1开始；然后2；2第一个未被访问的邻接点4；4第一个未被访问的邻接点8；8第一个未被访问的邻接点5；5的所有邻接点都被访问、则遍历标志数组、找到第一个未被访问的3；3第一个未被访问的邻接点6；6第一个未被访问的邻接点7；结束。

广度遍历 

对所有节点（1、2……8），假设从1开始访问，每访问一个节点，便将其标志数组（visited）对应位置置1，然后访问其所有未被访问的邻接点，接着对节点所有邻接点按顺序重复同样操作。若节点邻接点都被访问，则遍历标志数组，找到第一个未被访问的节点开始访问。

如上表：1开始；访问2、3；然后从1的第一个邻接点2开始、访问2的邻接点4、5；3开始、访问6、7；4开始、访问8；5开始、其所有邻接点都被访问、跳过；……

4 源代码示例

4.1 深度优先

#include <stdio.h>
#include <stdlib.h>#define MAX_VERTEX_NUM 100 // 图中最大节点数
typedef char VertexType;// 边表节点
typedef struct node {VertexType adjvex; // 与顶点相连的邻接点下标(adjoin：邻接)struct node* next; // 指向顶点的下一个邻接点
} EdgeNode;// 顶点结构
typedef struct vnode {VertexType vex;      // 存储顶点名EdgeNode* firstedge; // 边表头指针，指向顶点第一个邻接点
} VertexNode, AdjList[MAX_VERTEX_NUM];typedef struct {AdjList adjlist; // 描述图结构的邻接表int vexnum;      // 节点的数目int edgenum;     // 边的数目
} ALGraph;           // adjacency list：邻接表void CreateALG(ALGraph* ALG);     // 邻接表法创建图
void TraverseALG(ALGraph ALG);    // 输出图ALG的邻接表
void DFSTraverseALG(ALGraph ALG); // 深度优先遍历以邻接表存储的图ALG
void DFSALG(ALGraph ALG, int i);  // 以Vi为出发点对邻接表存储的图ALG开始DFS搜索
// 定位节点vertex，并将其下标赋给index
void LocateVex(ALGraph ALG, VertexType vertex, int* index);
int visited[MAX_VERTEX_NUM]; // 标志数组int main(void)
{ALGraph g;CreateALG(&g);printf("------------------------------\n");printf("vexnum = %d ; edgenum = %d\n", g.vexnum, g.edgenum);printf("------------------------------\n");TraverseALG(g);printf("------------------------------\n");DFSTraverseALG(g);return 0;
}
void CreateALG(ALGraph* ALG)
{VertexType ch;int i = 0, count = 0;EdgeNode* temp;printf("请输入图的顶点：");// 建立顶点表while ((ch = getchar()) != '\n') {ALG->adjlist[i].vex = ch;ALG->adjlist[i].firstedge = NULL;i++;}ALG->vexnum = i; // 顶点数// 头插法建立顶点的邻接边表for (i = 0; i < ALG->vexnum; i++) {printf("请输入顶点 %c 的邻接顶点：", ALG->adjlist[i].vex);// 按下回车结束邻接点的创建while ((ch = getchar()) != '\n') {temp = (EdgeNode*)malloc(sizeof(EdgeNode));temp->adjvex = ch;temp->next = ALG->adjlist[i].firstedge;ALG->adjlist[i].firstedge = temp;count++;}}// 无向图中每条边连接两个顶点，故：节点总度数 = 边数 * 2ALG->edgenum = count / 2;
}
void TraverseALG(ALGraph ALG)
{int i;EdgeNode* temp;if (ALG.vexnum == 0) {printf("图为空\n");return;}// 遍历图for (i = 0; i < ALG.vexnum; i++) {printf("顶点 %c ：", ALG.adjlist[i].vex);temp = ALG.adjlist[i].firstedge;// 输出图的信息while (temp) {printf("[ %c ] -> ", temp->adjvex);temp = temp->next;}printf("NULL\n");}
}
// 深度优先遍历以邻接表存储的图ALG
void DFSTraverseALG(ALGraph ALG)
{int i;// 初始化标志数组for (i = 0; i < ALG.vexnum; i++) {visited[i] = 0;}printf("图的深度优先遍历序列：");// 从第一个节点开始DFS搜索for (i = 0; i < ALG.vexnum; i++) {if (!visited[i]) {DFSALG(ALG, i);}}
}
// 以下标为i的节点为出发点对图ALG开始DFS搜索
void DFSALG(ALGraph ALG, int i)
{EdgeNode* temp;int index;printf("%c, ", ALG.adjlist[i].vex);visited[i] = 1; // 标记节点i已被访问temp = ALG.adjlist[i].firstedge;while (temp) {LocateVex(ALG, temp->adjvex, &index);// 若以index为下标的节点未被遍历，则遍历。并从该节点开始进行下一轮DFS搜索if (!visited[index]) {DFSALG(ALG, index);}// 若以index为下标的节点被遍历，则寻找节点的下一个邻接点temp = temp->next;}
}
void LocateVex(ALGraph ALG, VertexType vertex, int* index)
{int i;for (i = 0; i < ALG.vexnum; i++) {if (ALG.adjlist[i].vex == vertex) {*index = i; // 将节点vertex的下标赋给indexreturn;}}
}

C:\WINDOWS\system32\cmd.exe /c (gcc -fexec-charset=gbk 1.c -o 1 ^&^& 1 ^&^& del 1.exe)
请输入图的顶点：12345678
请输入顶点 1 的邻接顶点：32
请输入顶点 2 的邻接顶点：541
请输入顶点 3 的邻接顶点：761
请输入顶点 4 的邻接顶点：82
请输入顶点 5 的邻接顶点：82
请输入顶点 6 的邻接顶点：73
请输入顶点 7 的邻接顶点：63
请输入顶点 8 的邻接顶点：54
------------------------------
vexnum = 8 ; edgenum = 9
------------------------------
顶点 1 ：[ 2 ] -> [ 3 ] -> NULL
顶点 2 ：[ 1 ] -> [ 4 ] -> [ 5 ] -> NULL
顶点 3 ：[ 1 ] -> [ 6 ] -> [ 7 ] -> NULL
顶点 4 ：[ 2 ] -> [ 8 ] -> NULL
顶点 5 ：[ 2 ] -> [ 8 ] -> NULL
顶点 6 ：[ 3 ] -> [ 7 ] -> NULL
顶点 7 ：[ 3 ] -> [ 6 ] -> NULL
顶点 8 ：[ 4 ] -> [ 5 ] -> NULL
------------------------------
图的深度优先遍历序列：1, 2, 4, 8, 5, 3, 6, 7, Hit any key to close this window...

4.2广度优先

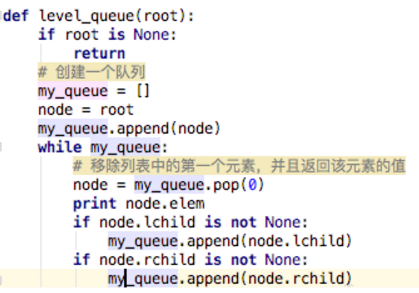
广度优先遍历时，需要用队列辅助操作，关于队列的实现，可参考我的博客C语言实现顺序队列、循环队列、链式队列。

#include <stdio.h>
#include <stdlib.h>#define MAX_VERTEX_NUM 100 // 图中最大节点数
typedef char VertexType;   // 定义节点名为char型
// 边表节点
typedef struct node {VertexType adjvex; // 与顶点相连的邻接点下标(adjoin：邻接)struct node* next; // 指向顶点的下一个邻接点
} EdgeNode;// 顶点结构
typedef struct vnode {VertexType vex;      // 存储顶点名EdgeNode* firstedge; // 边表头指针，指向顶点第一个邻接点
} VertexNode, AdjList[MAX_VERTEX_NUM];// 描述图结构的邻接表
typedef struct {AdjList adjlist;int vexnum;  // 节点的数目int edgenum; // 边的数目
} ALGraph;       // adjacency list：邻接表int visited[MAX_VERTEX_NUM]; // 标志数组void CreateALG(ALGraph* ALG);     // 邻接表法创建图
void TraverseALG(ALGraph ALG);    // 输出图ALG的邻接表
void BFSTraverseALG(ALGraph ALG); // 广度优先遍历以邻接表存储的图ALG
// 定位节点vertex，并将其下标赋给index
void LocateVex(ALGraph ALG, VertexType vertex, int* index);/*----------------定义一个循环队列-------------------*/
#define CQ_INIT_SIZE 100 // 队列初始容量
typedef int dataType;
typedef struct {dataType* data; //存储队列元素int front;      //指向队列中第一个元素int rear;       //指向队列中最后一个元素下一位置int cqCapacity; //最多能容纳的元素个数(队列容量)
} CQueue;CQueue* initCQueue();            //创建一个空循环队列
int push(CQueue* Q, dataType x); //将元素x入队。操作成功返回1，失败返回0
int pop(CQueue* Q, dataType* x); //队首元素出队，并将其值赋给x。操作成功返回1，失败返回0
int isEmpty(CQueue* Q);          //队列空返回1，否则返回0
int isFull(CQueue* Q);           //队列满返回1，否则返回0int main(void)
{ALGraph g;CreateALG(&g);printf("------------------------------\n");printf("vexnum = %d ; edgenum = %d\n", g.vexnum, g.edgenum);printf("------------------------------\n");TraverseALG(g);printf("------------------------------\n");BFSTraverseALG(g);return 0;
}void CreateALG(ALGraph* ALG)
{VertexType ch;int i = 0, count = 0;EdgeNode* temp;printf("请输入图的顶点：");// 建立顶点表while ((ch = getchar()) != '\n') {ALG->adjlist[i].vex = ch;ALG->adjlist[i].firstedge = NULL;i++;}ALG->vexnum = i; // 顶点数// 头插法建立顶点的邻接边表for (i = 0; i < ALG->vexnum; i++) {printf("请输入顶点 %c 的邻接顶点：", ALG->adjlist[i].vex);// 按下回车结束邻接点的创建while ((ch = getchar()) != '\n') {temp = (EdgeNode*)malloc(sizeof(EdgeNode));temp->adjvex = ch;temp->next = ALG->adjlist[i].firstedge;ALG->adjlist[i].firstedge = temp;count++;}}ALG->edgenum = count / 2;// 无向图中每条边连接两个顶点，故：节点总度数 = 边数 * 2
}void TraverseALG(ALGraph ALG)
{int i;EdgeNode* index;// 若图为空，则停止遍历if (ALG.vexnum == 0) {printf("图为空\n");return;}// 遍历图for (i = 0; i < ALG.vexnum; i++) {printf("顶点 %c ：", ALG.adjlist[i].vex);index = ALG.adjlist[i].firstedge;// 以邻接表形式输出图的信息while (index) {printf("[ %c ] -> ", index->adjvex);index = index->next;}printf("NULL\n");}
}// 广度优先遍历以邻接表存储的图ALG
void BFSTraverseALG(ALGraph ALG)
{int i, index; // index为当前访问节点的索引char ch;      // 从节点ch开始对图进行BFS搜索EdgeNode* temp;CQueue* que = initCQueue();// 初始化标志数组for (i = 0; i < ALG.vexnum; i++) {visited[i] = 0;}printf("请输入开始节点：");scanf("%c", &ch);LocateVex(ALG, ch, &index); // 将开始节点ch的下标赋给indexprintf("图的广度优先遍历序列：");if (!visited[index]) {push(que, index); // 开始节点入队，并修改visited数组visited[index] = 1;// 当队列不空时while (!isEmpty(que)) {pop(que, &index); // 队首元素出队并访问printf("%c, ", ALG.adjlist[index].vex);temp = ALG.adjlist[index].firstedge;// 将节点的所有邻接点入队while (temp) {LocateVex(ALG, temp->adjvex, &index);// 若节点未被遍历，则入队并修改visited数组if (!visited[index]) {push(que, index);visited[index] = 1;}temp = temp->next;}}}
}void LocateVex(ALGraph ALG, VertexType vertex, int* index)
{int i;for (i = 0; i < ALG.vexnum; i++) {if (ALG.adjlist[i].vex == vertex) {*index = i; // 将节点vertex的下标赋给indexreturn;}}printf("节点 %c 定位失败！\n", vertex);
}// 建立空队列
CQueue* initCQueue()
{CQueue* Q = (CQueue*)malloc(sizeof(CQueue));Q->data = (dataType*)malloc(CQ_INIT_SIZE * sizeof(dataType));Q->front = 0;Q->rear = 0;Q->cqCapacity = CQ_INIT_SIZE;return Q;
}
int isFull(CQueue* Q)
{return (Q->rear + 1) % Q->cqCapacity == Q->front ? 1 : 0;
}int isEmpty(CQueue* Q)
{return Q->front == Q->rear ? 1 : 0;
}
// 入队
int push(CQueue* Q, dataType x)
{if (isFull(Q)) {// 若达到最大容量，则将新容量扩大至旧容量 1.5 倍int increment = Q->cqCapacity / 2;Q->data = (dataType*)realloc(Q->data,(Q->cqCapacity + increment) * sizeof(dataType));if (!Q->data) {return 0;}Q->cqCapacity += increment;}Q->data[Q->rear] = x;Q->rear = (Q->rear + 1) % Q->cqCapacity;return 1;
}
// 出队
int pop(CQueue* Q, dataType* x)
{if (isEmpty(Q)) {return 0;} else {*x = Q->data[Q->front];Q->front = (Q->front + 1) % Q->cqCapacity;return 1;}
}


C:\WINDOWS\system32\cmd.exe /c (gcc -fexec-charset=gbk 1.c -o 1 ^&^& 1 ^&^& del 1.exe)
请输入图的顶点：12345678
请输入顶点 1 的邻接顶点：32
请输入顶点 2 的邻接顶点：541
请输入顶点 3 的邻接顶点：761
请输入顶点 4 的邻接顶点：82
请输入顶点 5 的邻接顶点：82
请输入顶点 6 的邻接顶点：73
请输入顶点 7 的邻接顶点：63
请输入顶点 8 的邻接顶点：54
------------------------------
vexnum = 8 ; edgenum = 9
------------------------------
顶点 1 ：[ 2 ] -> [ 3 ] -> NULL
顶点 2 ：[ 1 ] -> [ 4 ] -> [ 5 ] -> NULL
顶点 3 ：[ 1 ] -> [ 6 ] -> [ 7 ] -> NULL
顶点 4 ：[ 2 ] -> [ 8 ] -> NULL
顶点 5 ：[ 2 ] -> [ 8 ] -> NULL
顶点 6 ：[ 3 ] -> [ 7 ] -> NULL
顶点 7 ：[ 3 ] -> [ 6 ] -> NULL
顶点 8 ：[ 4 ] -> [ 5 ] -> NULL
------------------------------
请输入开始节点：1
图的广度优先遍历序列：1, 2, 3, 4, 5, 6, 7, 8, Hit any key to close this window...


http://chatgpt.dhexx.cn/article/2bVoaCWc.shtml

相关文章

数据结构之深度优先和广度优先遍历

数据结构之深度优先和广度优先遍历

文章目录 图为什么要有图图的常用概念邻接矩阵邻接表图的深度优先遍历深度优先遍历基本思想深度优先遍历算法步骤深度优先算法的代码实现 图的广度优先遍历广度优先遍历基本思想广度优先遍历算法步骤广度优先算法的代码实现图结构完整代码 图 为什么要有图 1)前面我们学了线性…
阅读更多...
图的深度优先和广度优先遍历算法

图的深度优先和广度优先遍历算法

编写一个程序&#xff0c;输出下面带权有向图的邻接表&#xff0c;并根据该邻接表&#xff0c;实现图的遍历运算&#xff0c;具体要求如下&#xff1a; (1)从顶点0开始的深度优先遍历序列(递归算法) (2)从顶点0开始的深度优先遍历序列(非递归算法) (3)从顶点0开始的广度优先遍历…
阅读更多...
算法之深度优先、广度优先算法

算法之深度优先、广度优先算法

目录 前言&#xff1a; 搜索算法&#xff1a; 广度优先搜索算法 深度优先搜索算法 问题&#xff1a;如何找出社交网络中某个用户的三度好友关系&#xff1f; 总结&#xff1a; 参考资料&#xff1a; 前言&#xff1a; 图这种数据结构经常用于表示一个社交网络&#x…
阅读更多...
广度优先搜索与深度优先搜索

广度优先搜索与深度优先搜索

广度优先搜索&#xff08;宽度优先搜索&#xff0c;BFS&#xff09;和深度优先搜索&#xff08;DFS&#xff09;算法的应用非常广泛&#xff0c;本篇文章主要介绍BFS与DFS的原理、实现和应用。 深度优先搜索 图的深度优先搜索(Depth First Search)&#xff0c;和树的先序遍历…
阅读更多...
深度优先遍历与广度优先遍历

深度优先遍历与广度优先遍历

1、深度优先遍历(Depth First Search, 简称 DFS) 1.1、主要思路 从图中一个未访问的顶点 V 开始&#xff0c;沿着一条路一直走到底&#xff0c;然后从这条路尽头的节点回退到上一个节点&#xff0c;再从另一条路开始走到底…&#xff0c;不断递归重复此过程&#xff0c;直到所…
阅读更多...
深度优先与广度优先

深度优先与广度优先

深度优先遍历简称DFS&#xff08;Depth First Search&#xff09;&#xff0c;广度优先遍历简称BFS&#xff08;Breadth First Search&#xff09;&#xff0c;它们是遍历图当中所有顶点的两种方式。 深度优先遍历&#xff1a; 选取一个节点开始&#xff0c;沿着一条路一直走…
阅读更多...
深度优先遍历（DFS）和广度优先遍历（BFS）

深度优先遍历（DFS）和广度优先遍历（BFS）

深度优先遍历&#xff08;DFS&#xff09;和广度优先遍历&#xff08;BFS&#xff09; 图的遍历&#xff1a;所谓遍历&#xff0c;即是对结点的访问。一个图有多个结点&#xff0c;如何遍历这些结点&#xff0c;有两种访问策略&#xff1a; 深度优先遍历(Depth First Search, …
阅读更多...
深度优先与广度优先的区别！

深度优先与广度优先的区别！

从深度优先和广度优先两个角度解决同一个问题 题目 从一号顶点开始遍历这个图&#xff0c;使用深度优先搜索和广度优先搜索的2种遍历结果 深度优先遍历的主要思想就是&#xff0c;首先以一个未被访问过的顶点作为起始顶点&#xff0c;沿着当前顶点的边走到未访问过的顶点&…
阅读更多...
数据结构：图的遍历--深度优先、广度优先

数据结构：图的遍历--深度优先、广度优先

图的遍历&#xff1a;深度优先、广度优先 遍历 图的遍历是指从图中的某一顶点出发&#xff0c;按照一定的策略访问图中的每一个顶点。当然&#xff0c;每个顶点有且只能被访问一次。 在图的遍历中&#xff0c;深度优先和广度优先是最常使用的两种遍历方式。这两种遍历方式对无…
阅读更多...
深度优先搜索与广度优先搜索

深度优先搜索与广度优先搜索

算法是作用于具体数据结构之上的&#xff0c;深度优先搜索算法和广度优先搜索算法都是基于“图”这种数据结构的。这是因为&#xff0c;图这种数据结构的表达能力很强&#xff0c;大部分涉及搜索的场景都可以抽象成“图”。 图上的搜索算法&#xff0c;最直接的理解就是&#…
阅读更多...
广度优先搜索和深度优先搜索

广度优先搜索和深度优先搜索

文章目录 1. 前言2. 广度优先搜索和深度优先搜索1&#xff09;深度优先搜索2&#xff09;广度优先搜索 3. 深度优先搜索算法框架1&#xff09;二叉树深度优先搜索模板2&#xff09;图深度优先搜索模板3&#xff09;二维矩阵深度优先搜索模板 4. 广度优先搜索算法框架1&#xff…
阅读更多...
深度优先和广度优先算法

深度优先和广度优先算法

1、深度优先算法 遍历规则&#xff1a;不断地沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。 最后得出的结果为&#xff1a;ABDECFHG。 Python代码实现的伪代码如下&#xff1a; 2、广度优先算法&#xff1a; 遍历规则&#xff1a; 1&#xff09;先访问完当…
阅读更多...
深度优先搜索（DFS）和广度优先搜索（BFS）

深度优先搜索（DFS）和广度优先搜索（BFS）

代码随想录 深度优先搜索和广度优先搜索&#xff0c;都是图形搜索算法&#xff0c;它两相似&#xff0c;又却不同&#xff0c;在应用上也被用到不同的地方。这里拿一起讨论&#xff0c;方便比较。 先给大家说一下两者大概的区别&#xff1a; 如果搜索是以接近起始状态的程序依次…
阅读更多...
算法：深度优先和广度优先(DFS，BFS)

算法：深度优先和广度优先(DFS，BFS)

一丶深度优先&#xff08;DFS&#xff09; 深度优先顾名思义: 就是往深的地方优先查找或遍历。 如图二叉树&#xff0c;想遍历树中所有结点可以用中序遍历&#xff0c;前序或后序。如果某一结点还有子结点就会往深处就是往下一结点&#xff0c;一直遍历直到最后一个结点没有子…
阅读更多...
【算法】深度优先和广度优先

【算法】深度优先和广度优先

本文只是总结的相关概念&#xff0c;仅供自己复习&#xff0c;严禁转载&#xff0c;文末附有本文内容涉及的文章链接&#xff0c;请点开链接查看原文&#xff01; &#xff08;一&#xff09;深度优先 深度优先搜索属于图算法的一种&#xff0c;是一个针对图和树的遍历算法&am…
阅读更多...
算法：深度优先遍历和广度优先遍历

算法：深度优先遍历和广度优先遍历

什么是深度、广度优先遍历 图的遍历是指&#xff0c;从给定图中任意指定的顶点&#xff08;称为初始点&#xff09;出发&#xff0c;按照某种搜索方法沿着图的边访问图中的所有顶点&#xff0c;使每个顶点仅被访问一次&#xff0c;这个过程称为图的遍历。遍历过程中得到的顶点…
阅读更多...
ms17010利用失败解决一则

ms17010利用失败解决一则

没有反弹得到session并且提示如下&#xff1a; [-] 10.0.131.2:445 - Service failed to start, ERROR_CODE: 216 换了一个payload set payload windows/meterpreter/reverse_tcp set payload windows/x64/meterpreter/bind_tcp 就可以了。 如果遇到Unable to continue with i…
阅读更多...
永恒之蓝MS17010复现

永恒之蓝MS17010复现

MS17010复现 靶机win7&#xff1a;192.168.41.150 攻击kali: 192.168.41.147 扫描 通过auxiliary/scanner/smb/smb_ms17_010模块扫描虚拟机是否存在ms17010漏洞 存在 拿shell 通过exploit/windows/smb/ms17_010_eternalblue 直接exp打&#xff0c;设置好参数和payload,window…
阅读更多...
MS17010(永恒之蓝)漏洞利用与复现

MS17010(永恒之蓝)漏洞利用与复现

MS17010(永恒之蓝)漏洞利用与复现 0X00简介 永恒之蓝是指2017年4月14日晚&#xff0c;黑客团体Shadow Brokers&#xff08;影子经纪人&#xff09;公布一大批网络攻击工具&#xff0c;其中包含“永恒之蓝”工具&#xff0c;“永恒之蓝”利用Windows系统的SMB漏洞可以获取系统…
阅读更多...
网安学习记录1 ms17010漏洞

网安学习记录1 ms17010漏洞

使用nmap对win7进行端口扫描 进行ms17-010漏洞利用
阅读更多...
推荐文章

Copyright @ 2022~2023