二叉树遍历方法——前、中、后序遍历（图解）

article/2025/9/22 6:56:17

目录

 一、前序遍历

（1）递归版本

 （2）非递归版本

二、中序遍历

（1）递归版本

 （2）非递归版本

三、后序遍历

（1）递归版本

（2）非递归版本

四、总结

五、测试程序

六、程序输出

        二叉树的遍历是指按某条搜索路径访问树中的每个结点，使得每个结点均被访问一次，而且仅能访问一次（说明不可二次访问，一遍而过）。遍历一颗二叉树便要决定对根结点N、左子树L和右子树的访问顺序。 二叉树常的的遍历方法有前序遍历（NLR）、中序遍历（LNR）和后序遍历（LRN）三种遍历算法，其中 “序” 指的是根结点在何时被访问。三种遍历方法有递归和非递归两个版本。

二叉树的存储结构

typedef char Elemtype;  // 数据类型/*二叉树的链式存储结构*/
typedef struct BiTNode
{Elemtype data; // 数据域struct BiTNode* lchild, * rchild; // 左右孩子指针
}BiTNode, *BiTree;

 一、前序遍历

（1）递归版本

前序遍历的算法思路：
若二叉树为空，什么都不做，否则：

        i、先访问根结点；

        ii、再前序遍历左子树；

        iii、最后前序遍历右子树；

算法实现：

/*先序遍历*/
void PreOrder(BiTree T)
{if (T != NULL){ visit(T);              // 访问结点              PreOrder(T->lchild);   // 遍历结点左子树PreOrder(T->rchild);   // 遍历结点右子树}
}/*输出树结点*/
void visit(BiTree T)
{printf("树结点的值：%c\n", T->data);
}

         其中递归函数在计算机中实现隐式的利用了被称为调用栈的栈，即递归利用了栈，只是隐式的利用了栈，没有显示的让你看到其使用了栈，整体过程为访问结点并入栈遍历左子树，出栈遍历右子树。下面用图解的方法来对递归函数进行解说：

图解前序遍历的递归算法：

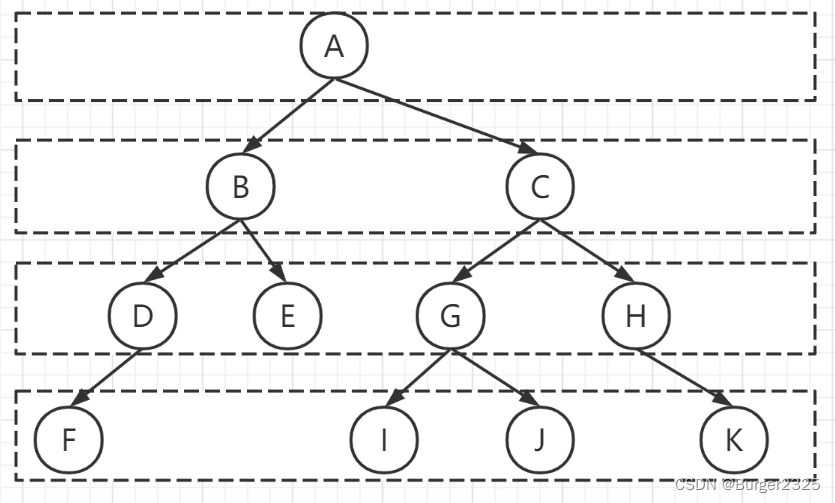
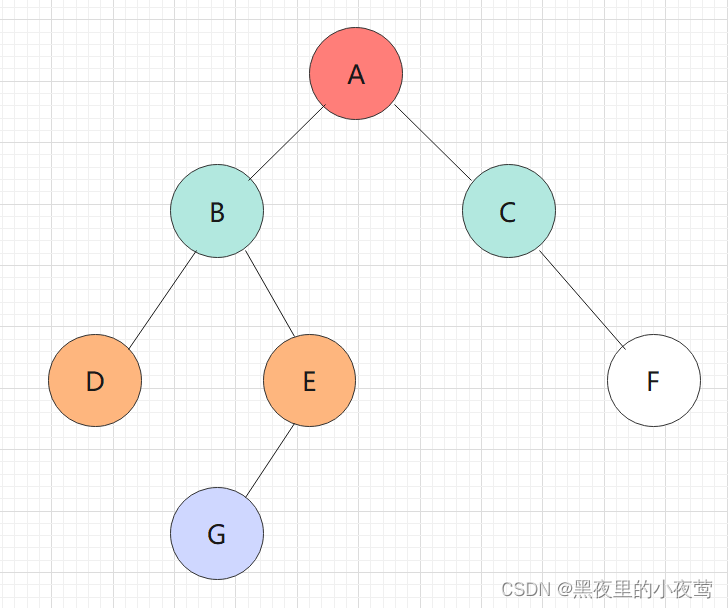
咱们看下面的二叉树是怎样利用递归函数实现前序遍历：

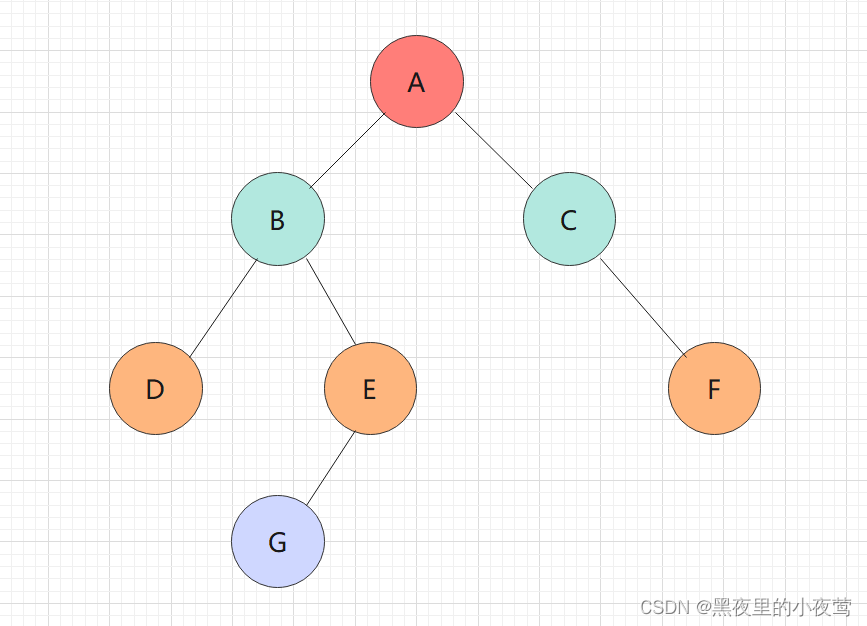
首先，T != NULL，遍历了A，并且指向A的指针入栈（递归的实现利用了栈），遍历A的左子树：

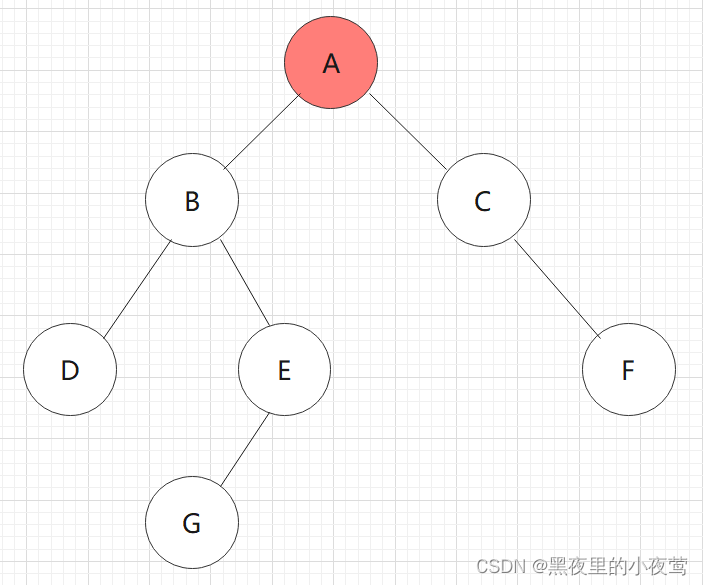
 A的左子树不为空，遍历B，并将B入栈，遍历B的左子树：

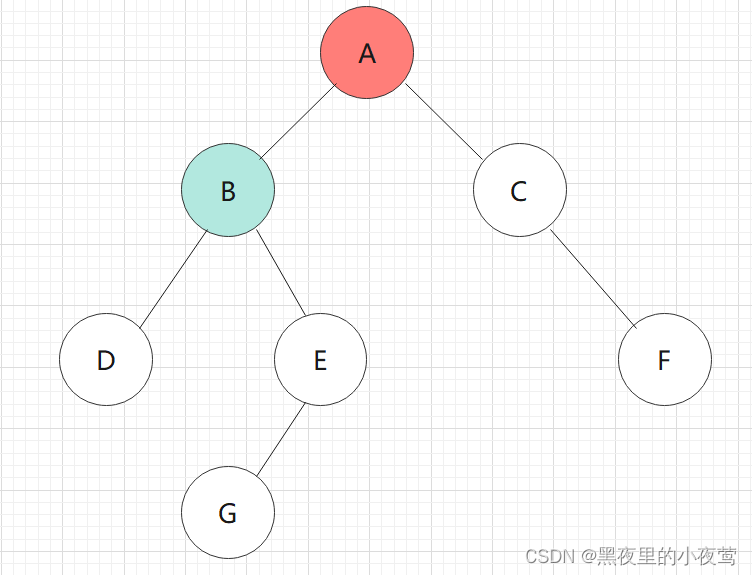
 B的左子树不为空，遍历D，并将D入栈，遍历D的左子树：

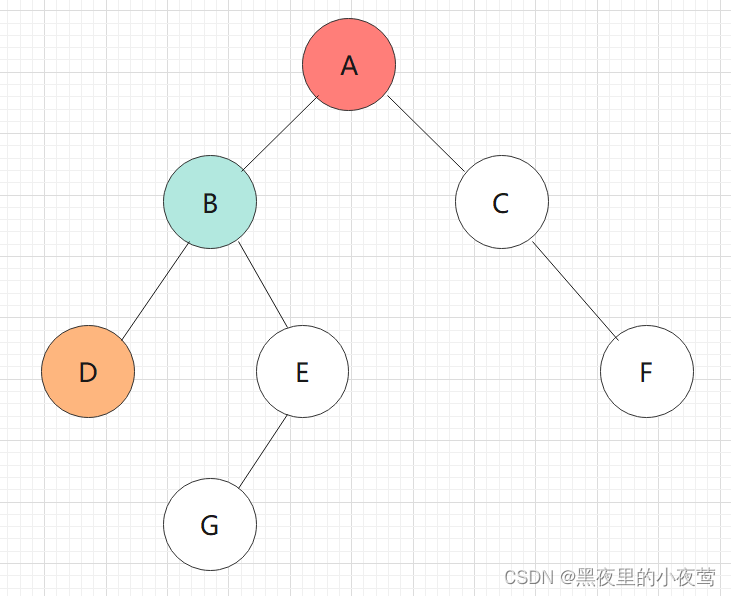
 D的左子树为空，不遍历，然后D出栈开始遍历D的右子树，但D的右子树也为空，不遍历，故D的左右子树，及其本身都遍历完。

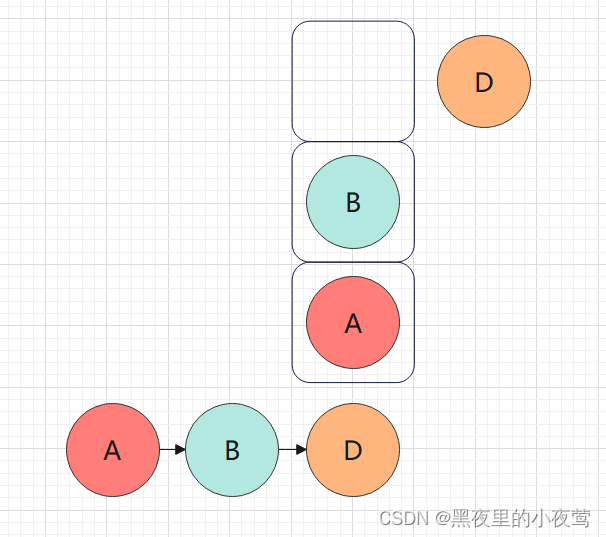
 然后B出栈，遍历B的右子树：

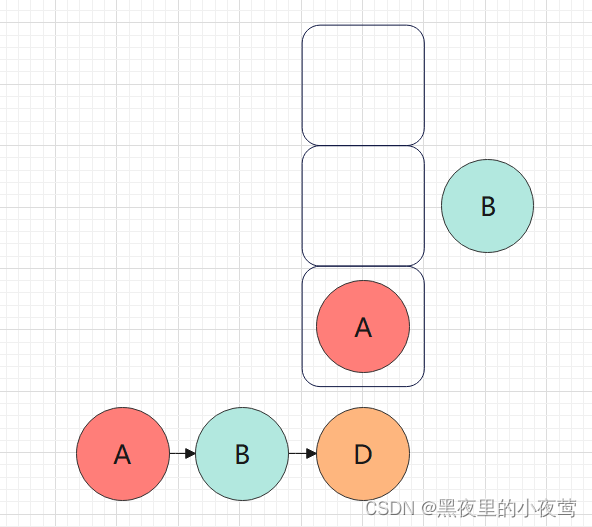
 B的右子树不为空，遍历E，E入栈，遍历E的左子树：

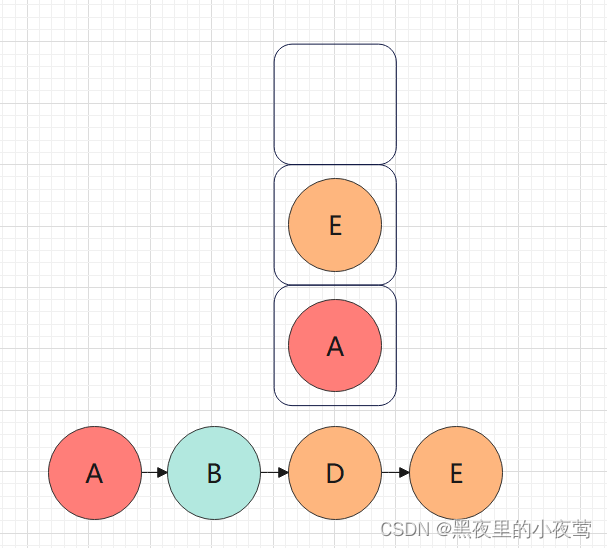
 E的左子树不为空，遍历G，G入栈，遍历G的左子树：

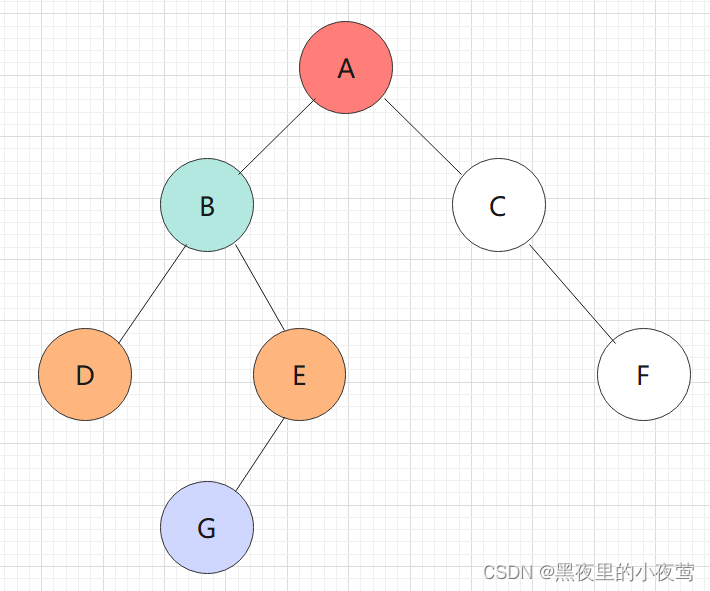
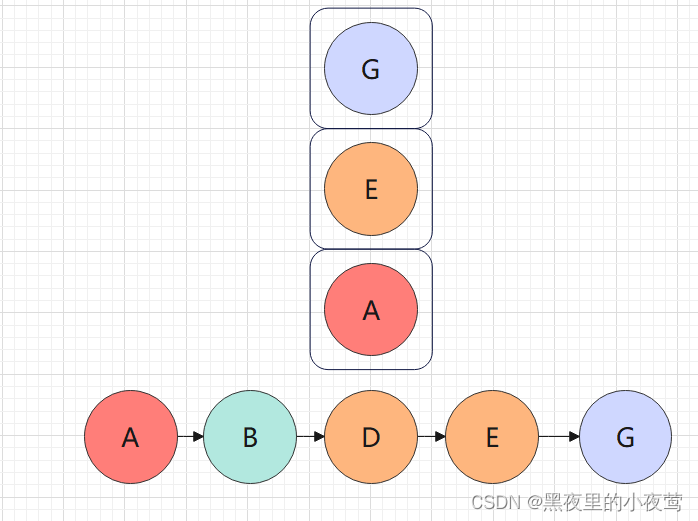
 G的左子树为空，不遍历，G出栈遍历G的右子树，但G的右子树为空，故也不进行遍历：

 此时，栈中有E、A结点，E出栈，遍历E的右子树，但E的右子树为空，故不进行遍历：

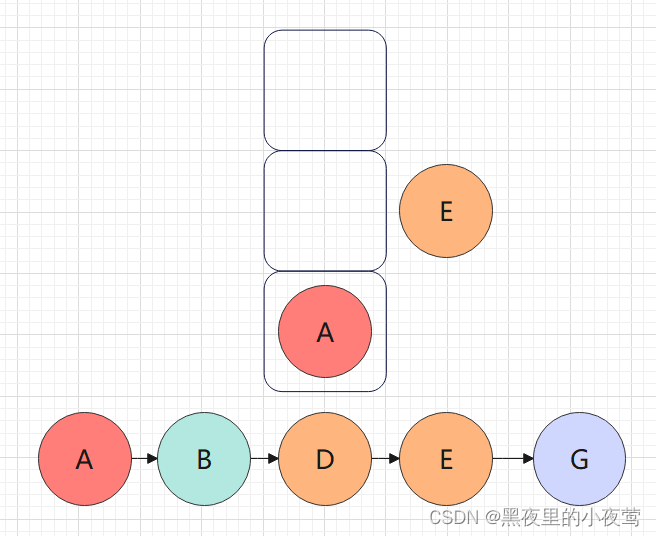
 然后A出栈，A的右子树不为空，遍历A的右子树：

 遍历C，C入栈，遍历C的左子树：

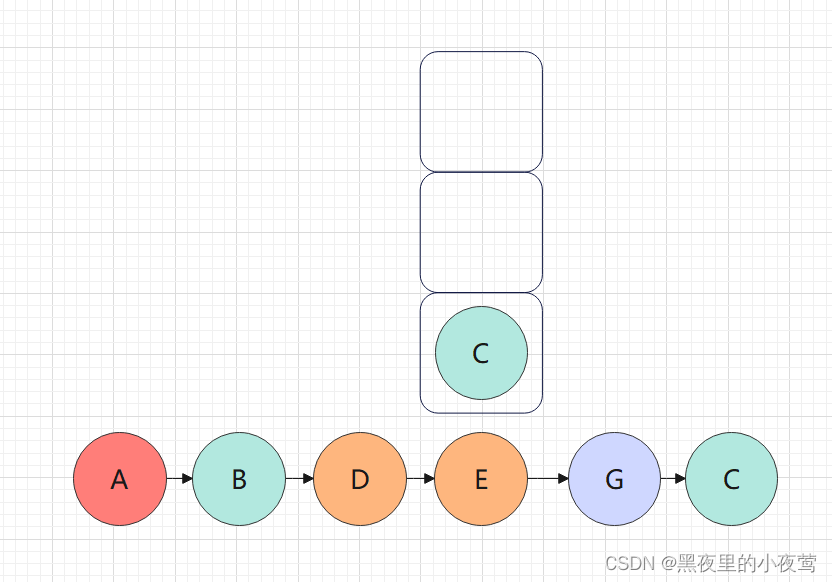
 C的左子树为空，不遍历，C出栈，遍历C的右子树：

 遍历F，F入栈，遍历F的左子树：

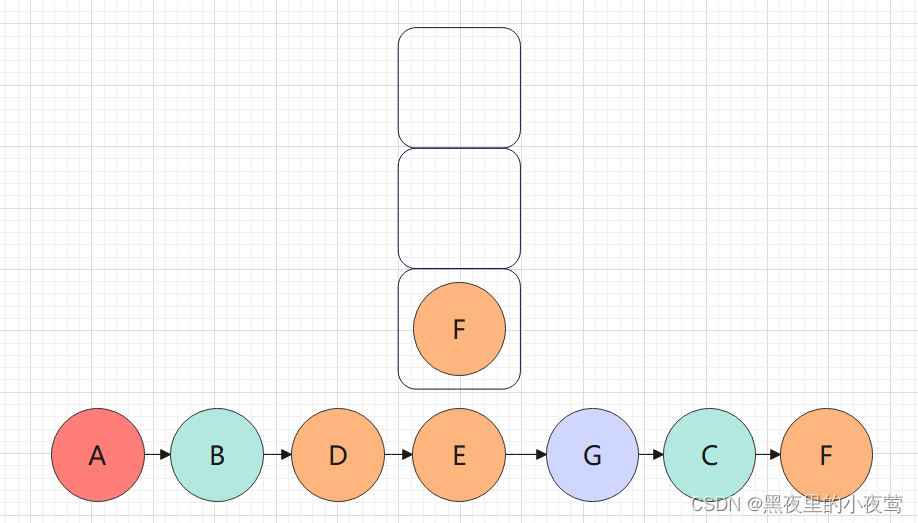
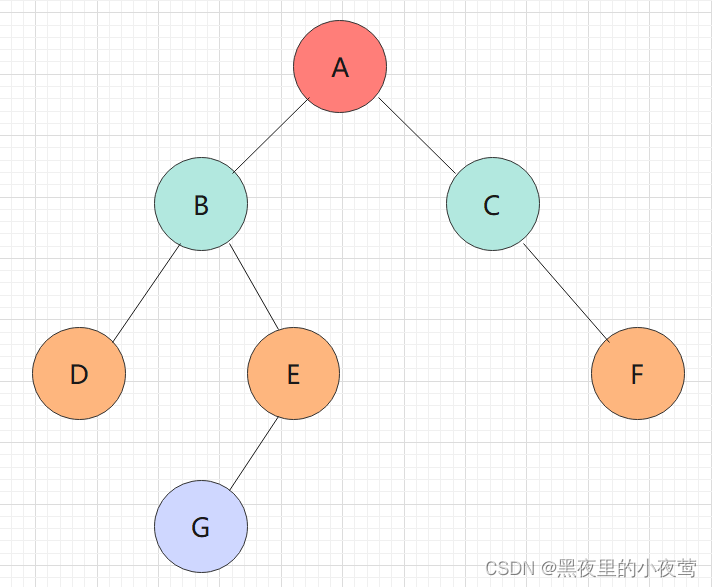
 F的左子树为空，不遍历，F出栈，遍历F的右子树：

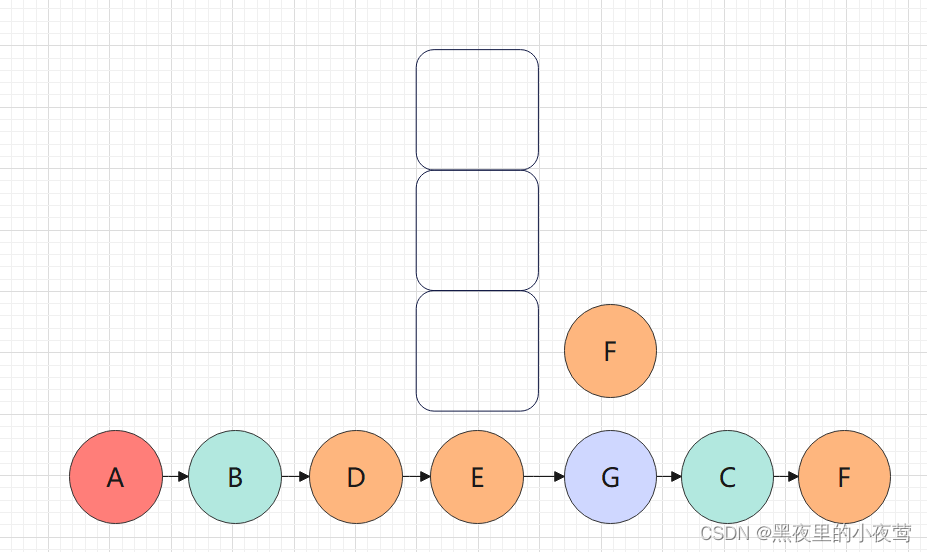
 F的右子树为空，不遍历，此时栈为空，结束遍历，二叉树的全部结点有且仅有一次被访问：

 前序遍历的结果为：

 （2）非递归版本

         前序遍历的非递归算法，就是将上面递归函数隐式调用栈的过程给显示表示出来，即利用一个辅助栈，来进行访问结点并入栈遍历左子树，结点出栈遍历右子树。

算法思路：

1、二叉树为空啥也不做；

2、结点不为空，访问并入栈，接着遍历其左子树；

3、结点为空但栈不为空，栈顶元素出栈，遍历栈顶元素的右子树；

4、结点为空并且栈为空结束遍历。

算法实现：

/*先序遍历*/
void PreOrder2(BiTree T)
{SqStack S;				  // 申请一个辅助栈InitStack(&S);			  // 初始化BiTree p = T;			  // p为遍历指针while (p || !IsEmpty(S))  // 栈不为空或p不为空时循环{if (p)			      // 一路向左{visit(p);		  // 访问当前节点，并入栈Push(&S, p);p = p->lchild;	  // 左孩子不空，一直向左走}else				  //出栈，并转向出栈结点的右子树{Pop(&S, &p);	  // 栈顶元素出栈p = p->rchild;    // 向右子树走，p赋值为当前结点的右孩子}					  // 返回while循环继续进入if-else语句}
}

其中栈的存储结构、初始化、入栈、出栈、判断栈空算法如下：

/*栈的存储结构*/
typedef struct Stack
{BiTree data[Maxsize]; // 存放栈中元素int top;		// 栈顶指针
}SqStack;
/*初始化栈*/
void InitStack(SqStack* S)
{S->top = -1;
}/*判断栈空*/
bool IsEmpty(SqStack S)
{if (S.top == -1)return true;elsereturn false;
}/*入栈*/
bool Push(SqStack* S, BiTree x)
{if (S->top == Maxsize - 1)   // 栈满return false;S->data[++(S->top)] = x;return true;
}/*出栈*/
bool Pop(SqStack* S, BiTree* x)
{if (S->top == -1) // 栈空return false;*x = S->data[(S->top)--];return true;
}

其图解过程和上面的递归利用调用栈的图解一致，故理解上面的图解，非递归前序遍历算法便可理解，其递归版本也知道其实际过程是怎么样的。

二、中序遍历

（1）递归版本

中序遍历算法思路：
二叉树为空，什么也不做，否则：

        i、中序遍历左子树；

        ii、访问根结点；

        iii、中序遍历右子树

算法实现：

/*中序遍历*/
void InOrder(BiTree T)
{if (T != NULL){InOrder(T->lchild);    // 遍历结点左子树visit(T);              // 访问结点InOrder(T->rchild);    // 遍历结点右子树}
}/*输出树结点*/
void visit(BiTree T)
{printf("树结点的值：%c\n", T->data);
}

        其中递归函数在计算机中实现隐式的利用了被称为调用栈的栈，即递归利用了栈，只是隐式的利用了栈，没有显示的让你看到其使用了栈，整体过程为结点入栈遍历左子树，出栈访问结点并遍历右子树。中序遍历和前序遍历基本思路是一致的，只是访问根结点的时间不同，中序遍历是遍历完左子树后再访问根结点，接着遍历右子树。下面用图解的方法来对递归函数进行解说： 

图解中序遍历二叉树：

首先看我们需要中序遍历这颗二叉树：

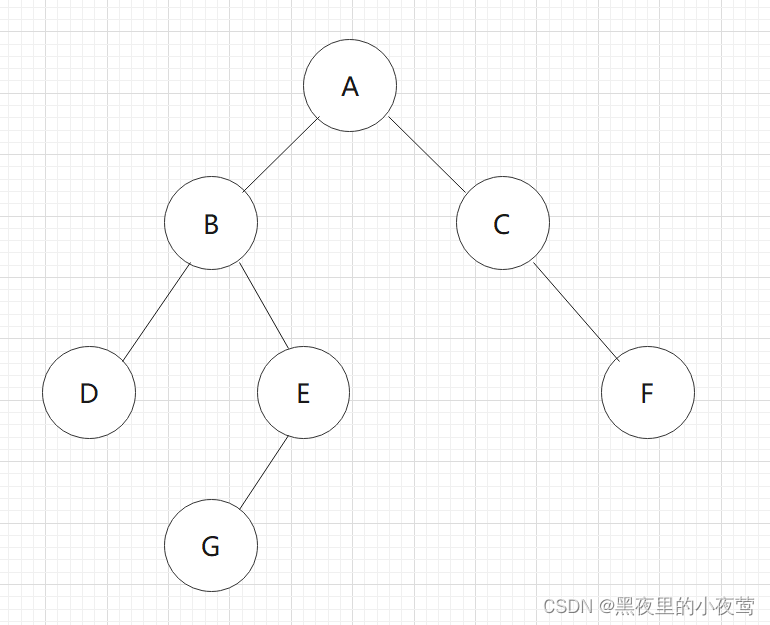
 T != NULL，将 A入栈，遍历A的左子树，但不遍历A，因为访问A的语句在遍历A的左子树之后：

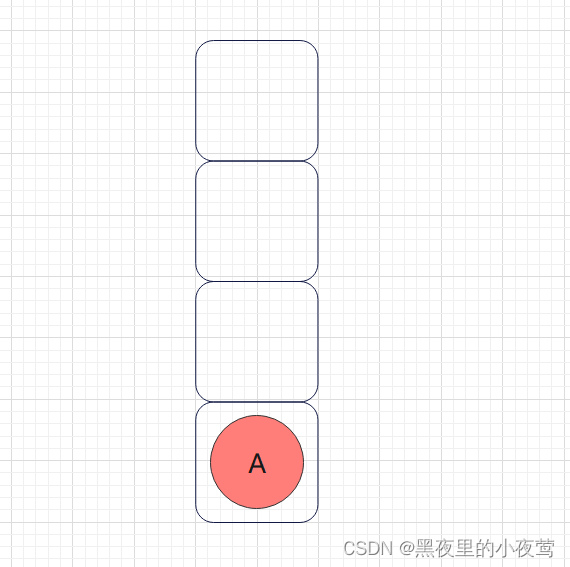
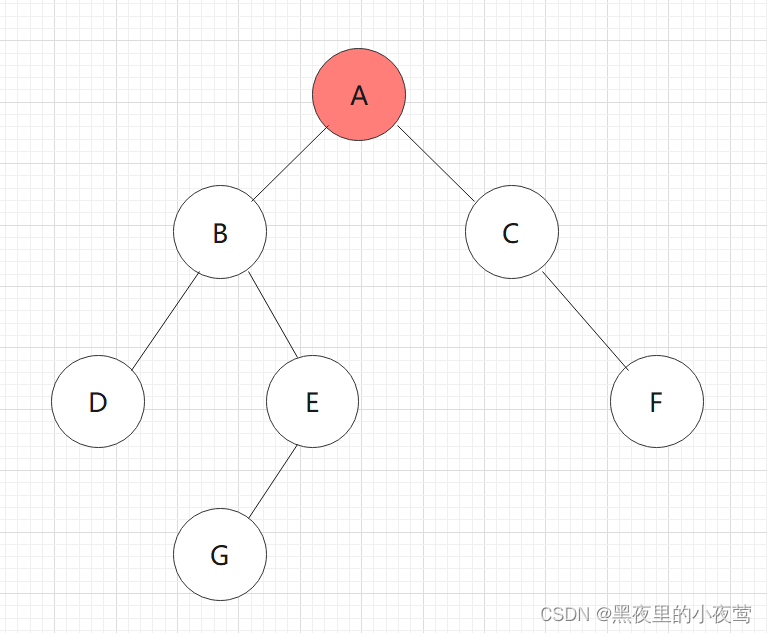
A的左子树不为空，B入栈，遍历B的左子树：

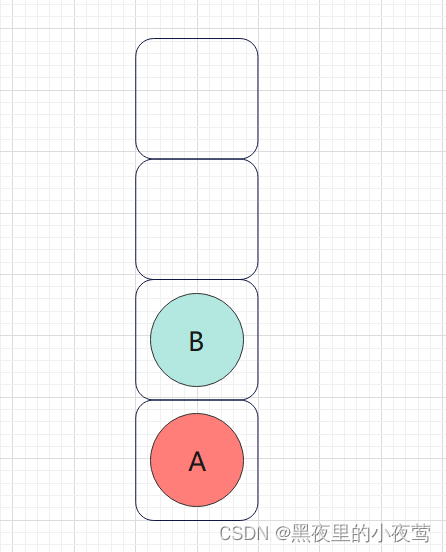
 B的左子树不为空，D入栈，遍历D的右子树：

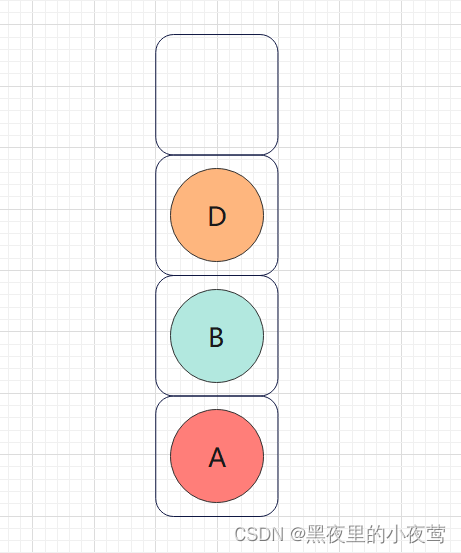
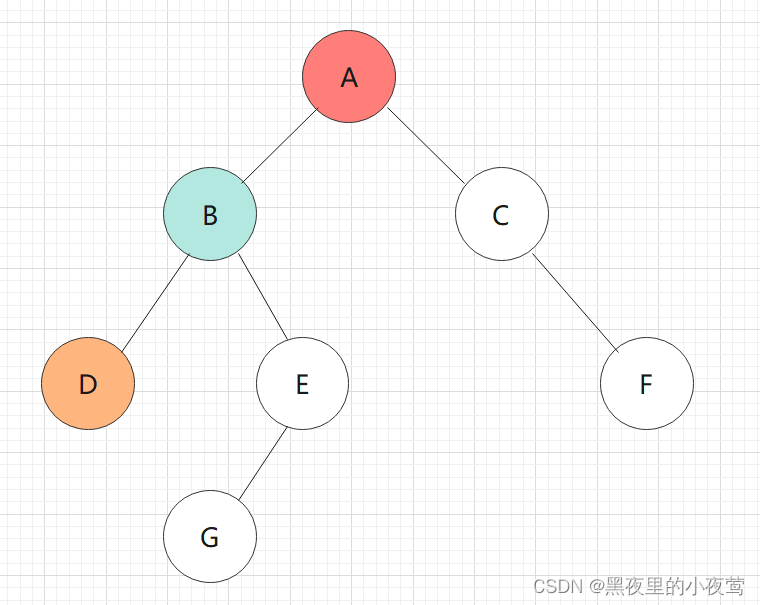
 D的左子树为空，不进行遍历，D出栈并访问D，接着遍历D的右子树：

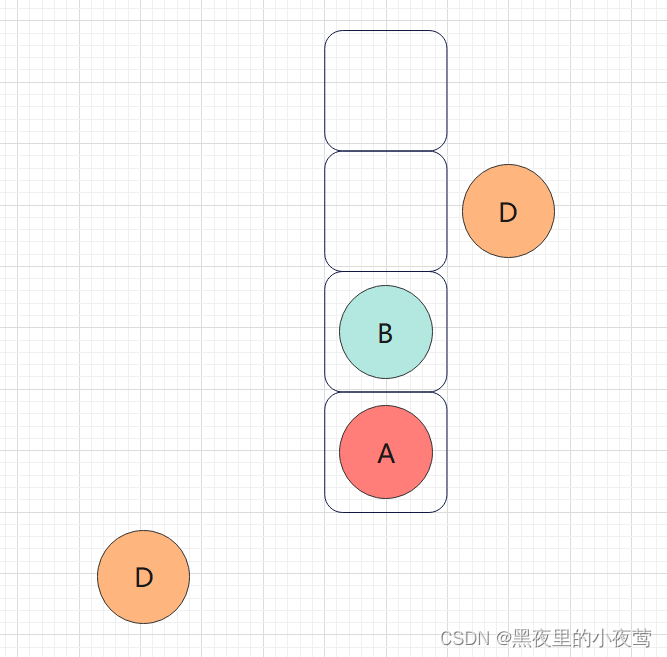
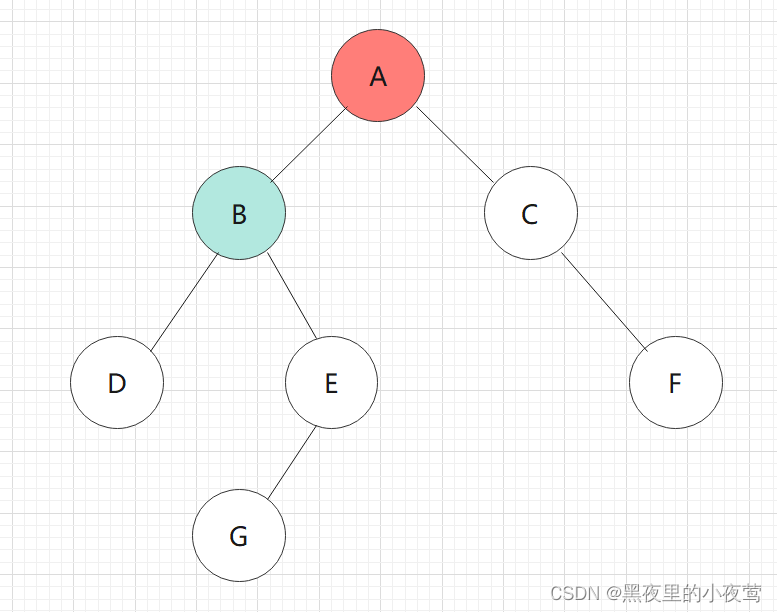
 D的右子树为空，不遍历，接着B出栈并访问，然后遍历B的右子树：

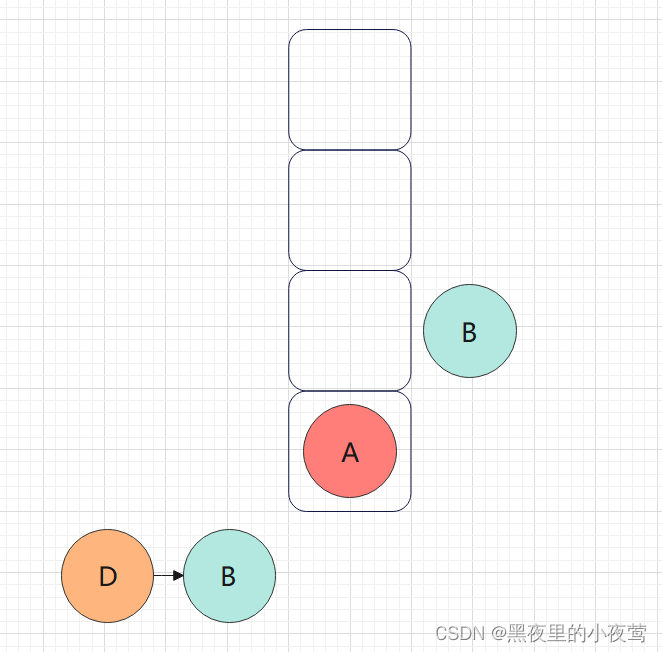
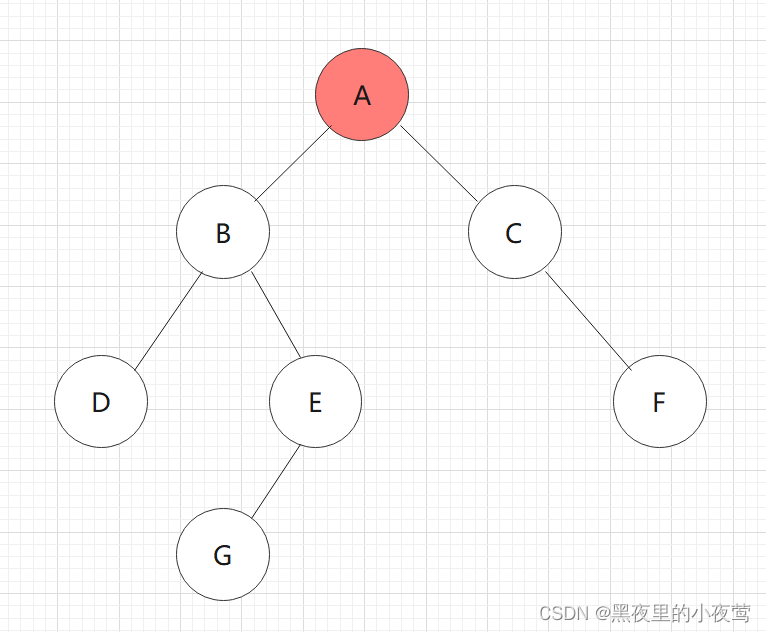
 B的右子树不为空，E入栈，遍历E的左子树：

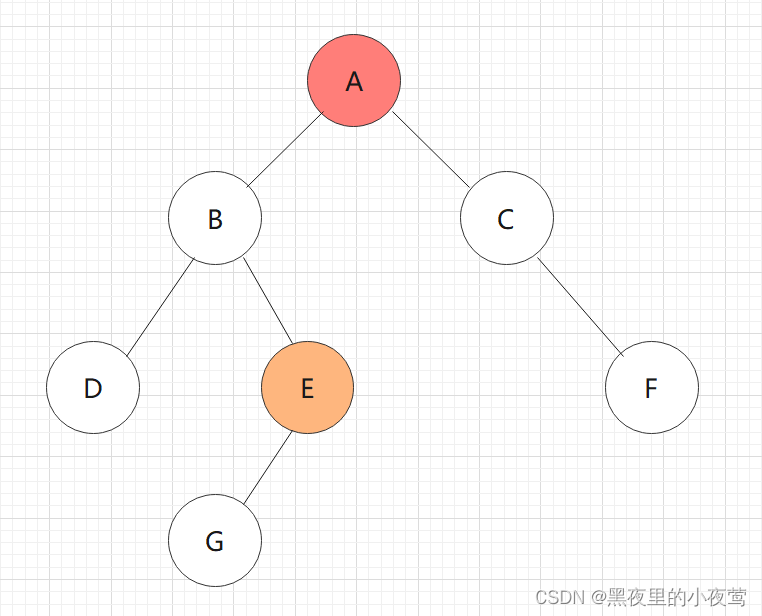
 E的左子树不为空，G入栈，遍历G的左子树：

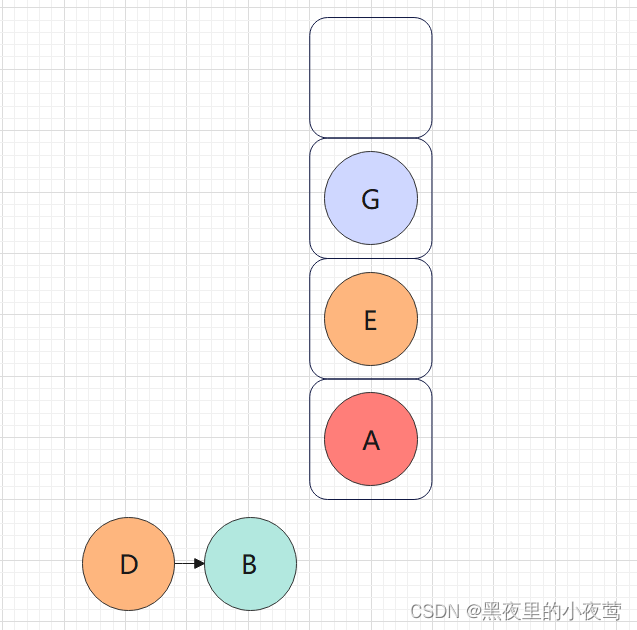
 G的左子树为空，不遍历，G出栈访问，接着遍历G的右子树：

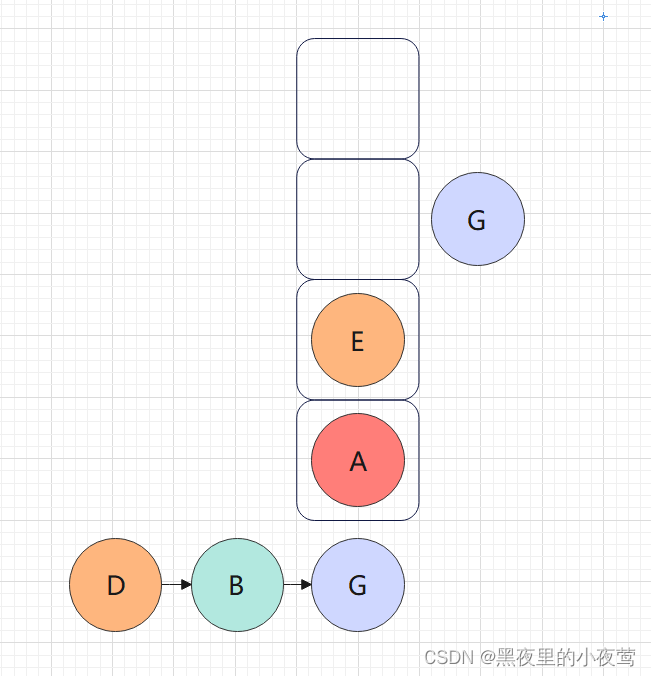
 G的右子树为空，不遍历，E出栈并访问，然后遍历E的右子树1：

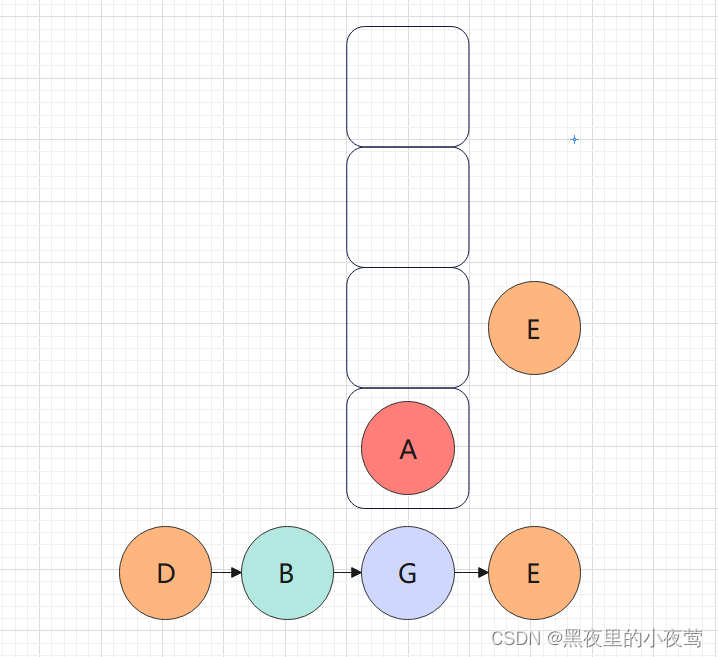
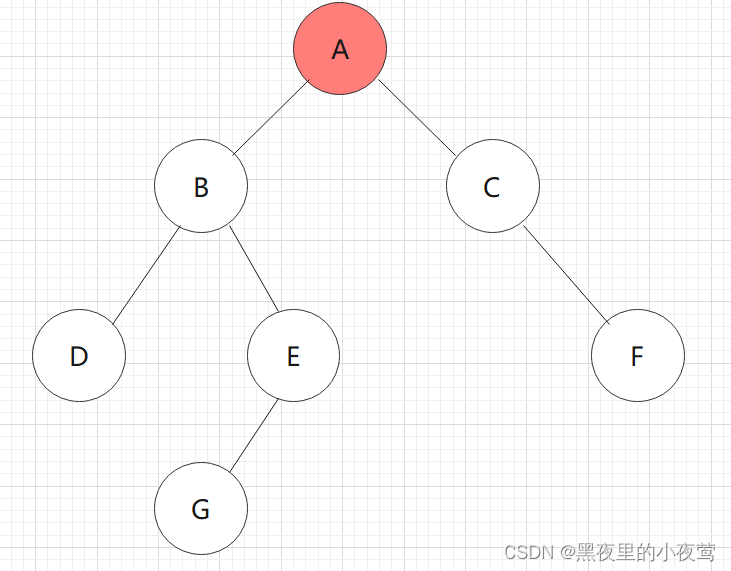
 E的右子树为空，不遍历，然后此时栈中只有A，A出栈并访问，接着遍历A的右子树：

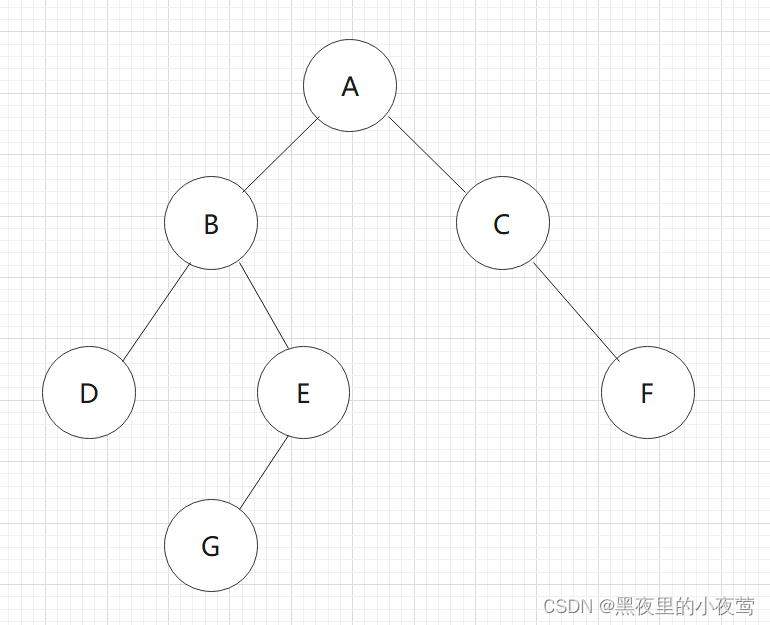
 此时已经遍历完左子树和根结点A，A的右子树不为空，C入栈，遍历C的左子树：

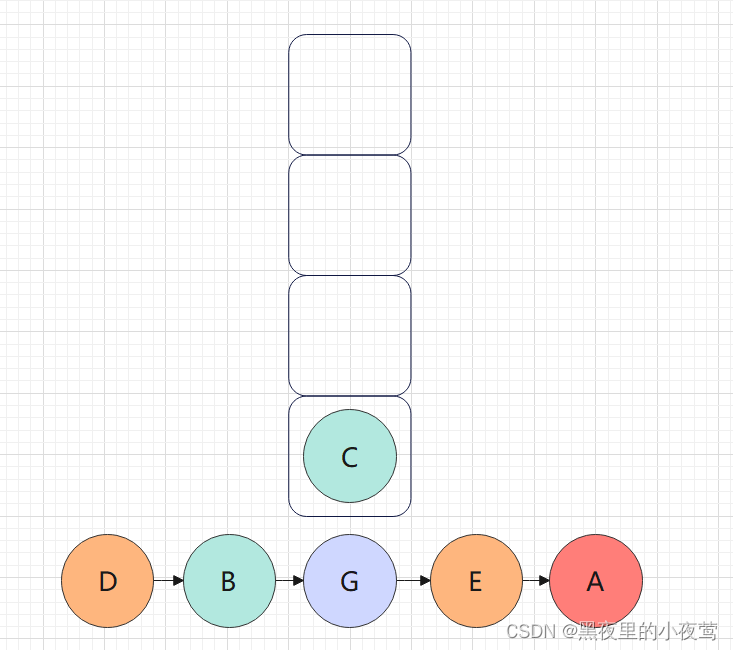
 C的左子树为空，不遍历，C出栈并访问，接着遍历C的右子树：

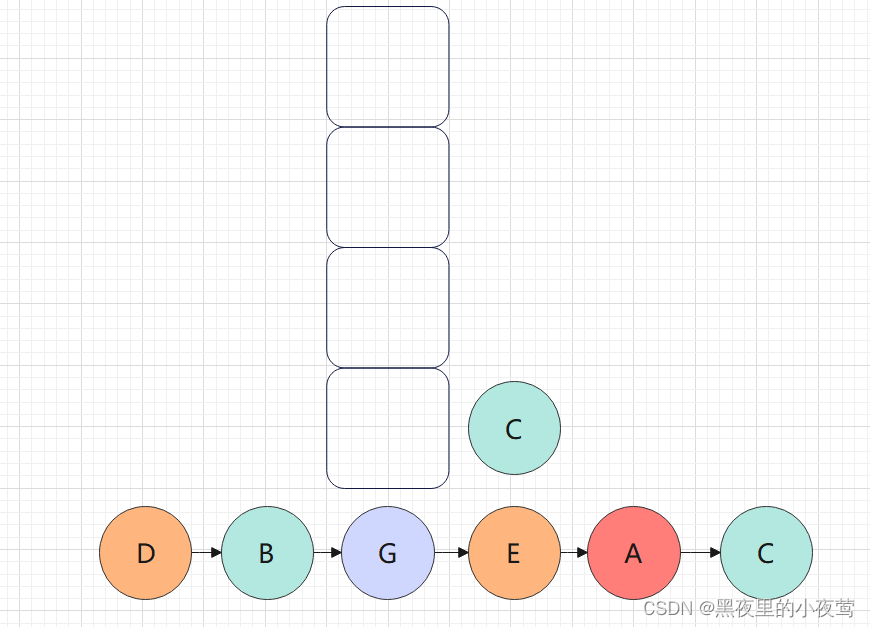
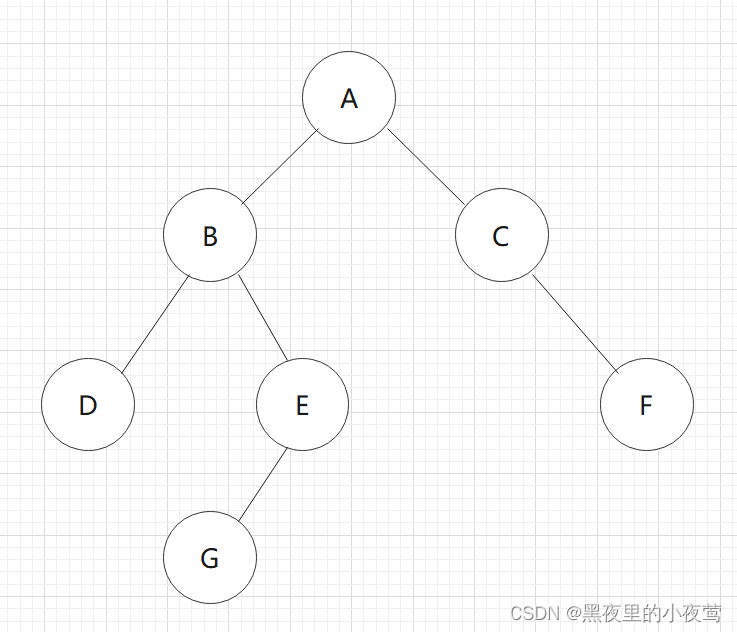
 C的右子树不为空，F入栈，遍历F的左子树：

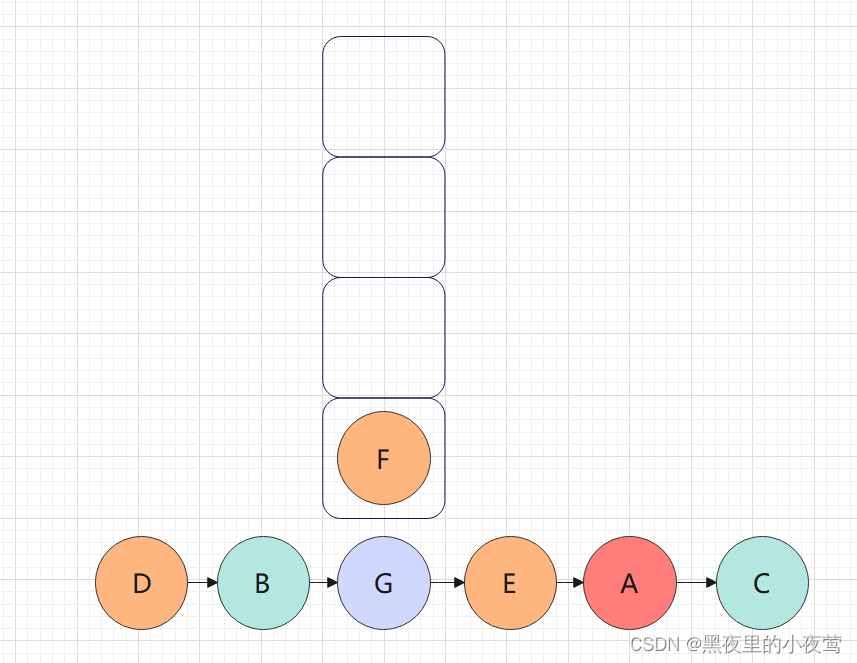
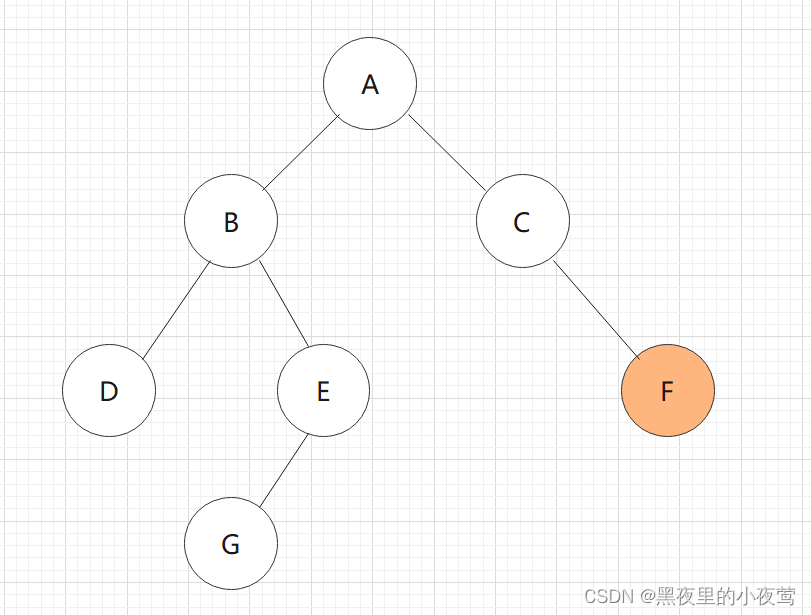
 F的左子树为空，不遍历，F出栈并访问，接着访问F的右子树：

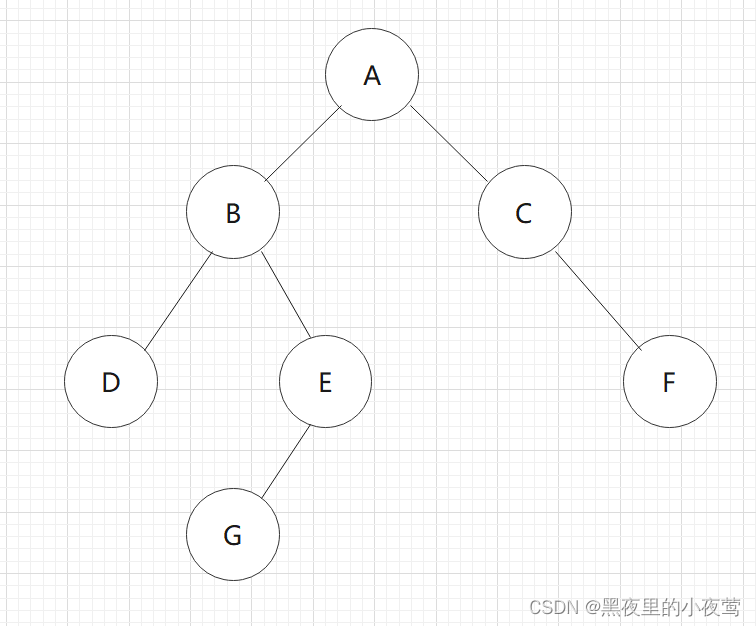
 F的右子树为空，不遍历，自此遍历结束，栈为空，并且二叉树的每个结点有且仅有一次被访问：

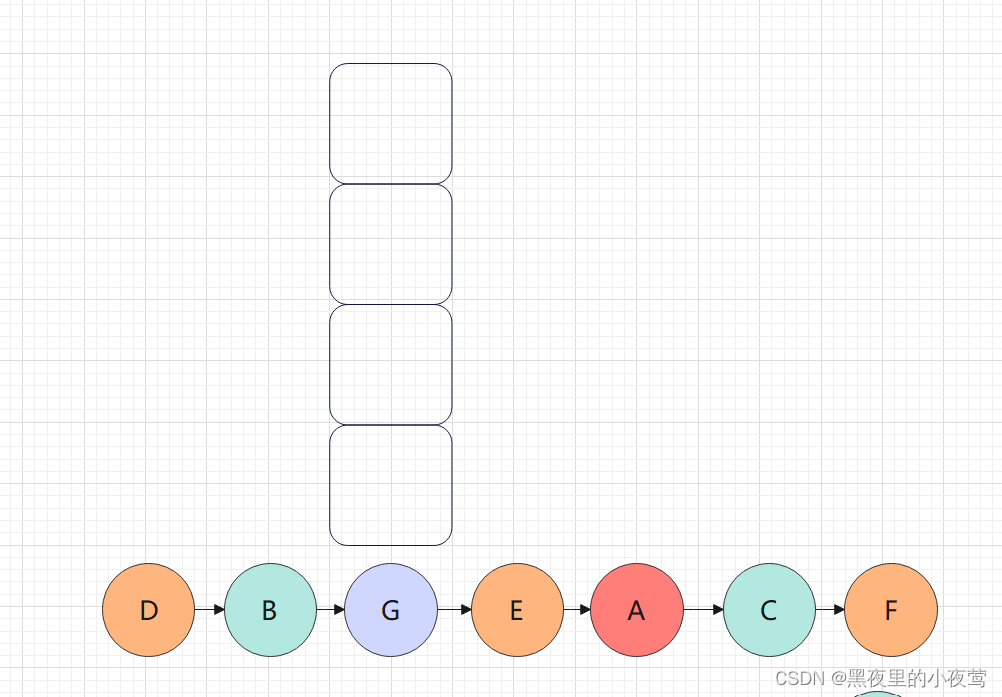
 中序遍历这颗二叉树的最终结果为：

 （2）非递归版本

        中序遍历的非递归算法，就是将上面递归函数隐式调用栈的过程给显示表示出来，即利用一个辅助栈，来进行结点入栈访问结点的左子树，出栈访问结点，并且遍历结点的右子树。

算法思路：

1、二叉树为空，啥也不做

2、结点不为空，入栈，并遍历其左子树

3、结点的左子树为空但栈不为空，栈顶元素出栈并访问，接着遍历栈顶元素的右子树；

4、栈为空，且结点也为空结束遍历。

算法实现：

/*中序遍历*/
void InOrder2(BiTree T)
{SqStack S;                  // 申请一个辅助栈InitStack(&S);				// 初始化BiTree p = T;				// p为遍历指针while (p || !IsEmpty(S))    // 栈不空或p不空时循环{if (p)					// 一路向左{Push(&S, p);        // 当前结点入栈p = p->lchild;		// 左孩子不空，一直向左走}else					// 出栈，并转向出栈结点的右子树{Pop(&S, &p);		// 栈顶元素出栈visit(p);			// 访问出栈结点p = p->rchild;		// 向右子树走，p赋值为当前结点的右孩子}						// 返回while循环继续进入if-else语句}
}

 其图解和上面的递归一致，这是只是把递归隐式调用栈的过程，给显现展示出来，理解了上面的图解，对这个非递归算法也是一目了然，同样也对递归的具体实现也掌握。

三、后序遍历

（1）递归版本

算法思路：

若二叉树为空，什么也不做，否则：

        i、后序遍历左子树

        ii、后序遍历右子树

        iii、访问根结点

 算法实现：

/*后序遍历*/
void PostOrder(BiTree T)
{if (T != NULL){PostOrder(T->lchild);	// 遍历结点左子树PostOrder(T->rchild);	// 遍历结点右子树visit(T);				// 访问结点}
}/*输出树结点*/
void visit(BiTree T)
{printf("树结点的值：%c\n", T->data);
}

        其中递归函数在计算机中实现隐式的利用了被称为调用栈的栈，即递归利用了栈，只是隐式的利用了栈，没有显示的让你看到其使用了栈，整体过程为结点入栈遍历左子树，出栈遍历右子树，紧接着入栈准备最后出栈的访问。后序遍历和中序遍历、前序遍历思路不太一致的，它是遍历完左子树和右子树后才遍历根结点，当其出栈遍历右子树（为了和前面的前序遍历、中序遍历出栈遍历右子树保持一致）还需要紧接着入栈进行最后的出栈自身遍历（递归函数最后一条语句visit(T)）（即相当于取这个元素来遍历右子树，但不出栈，遍历完右子树后再出栈访问）。下面用图解的方法来对以上思路解说：  

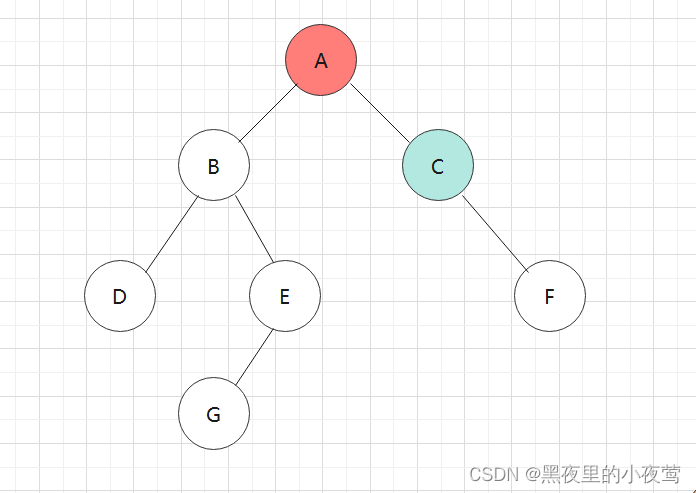
依然是利用和前序、中序遍历的二叉树：

 首先，T != NULL，A入栈进行遍历左子树：

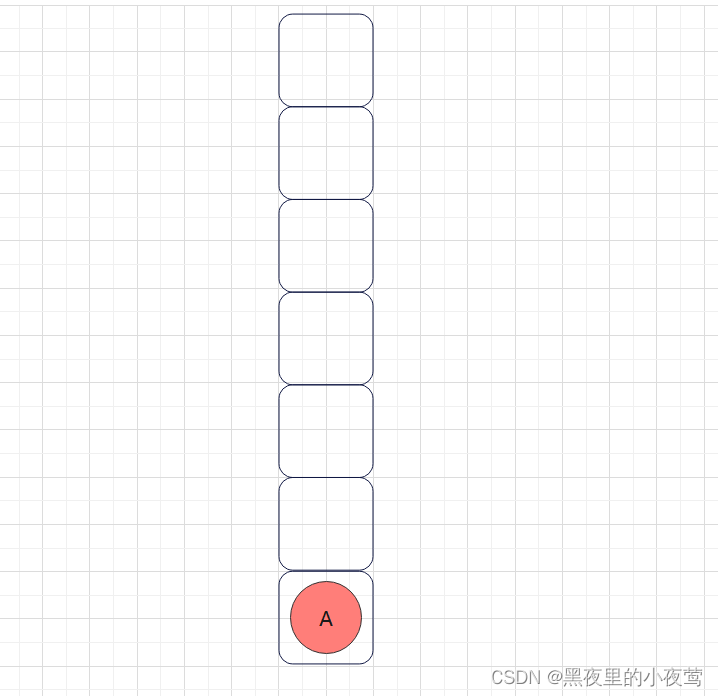
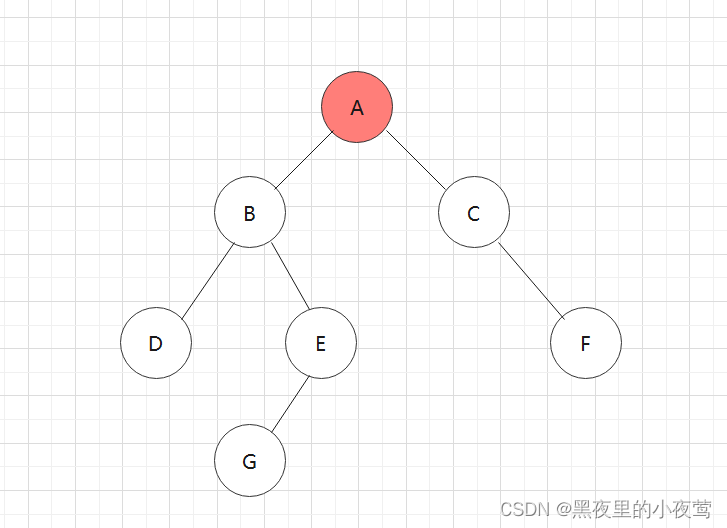
 A的左子树不为空，B入栈，遍历B的左子树：

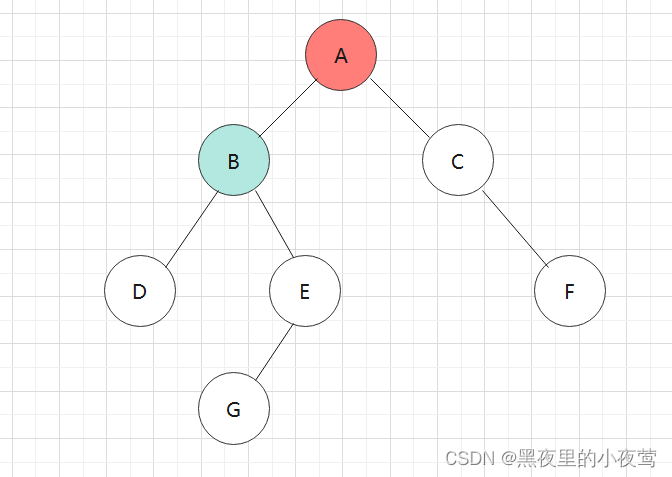
 B的左子树不为空，D入栈，遍历D的左子树：

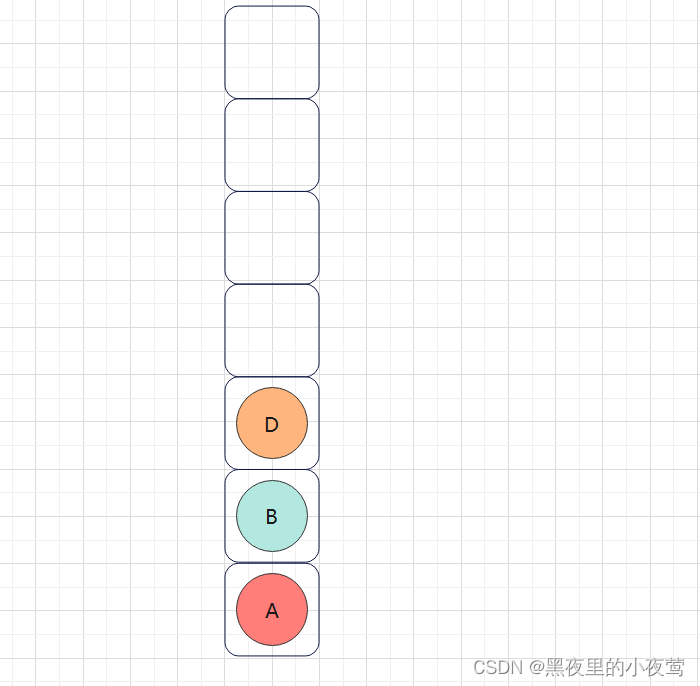
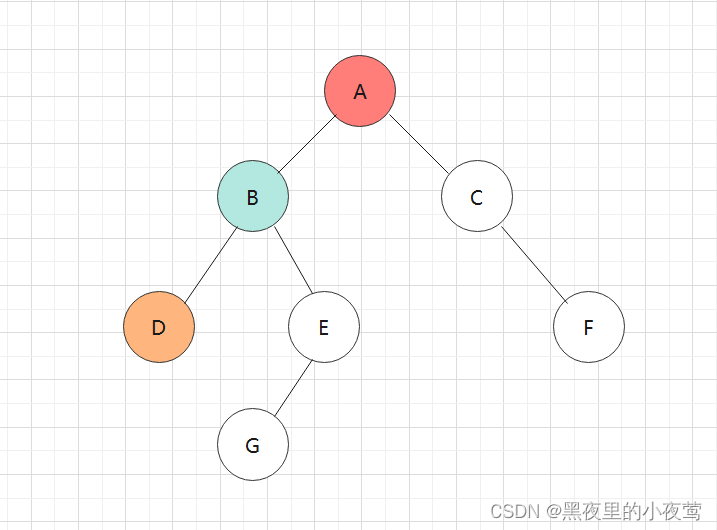
 D的左子树为空，不遍历，D出栈遍历D的右子树，但由于在函数最后还需遍历自身，故出栈后紧接着入栈：

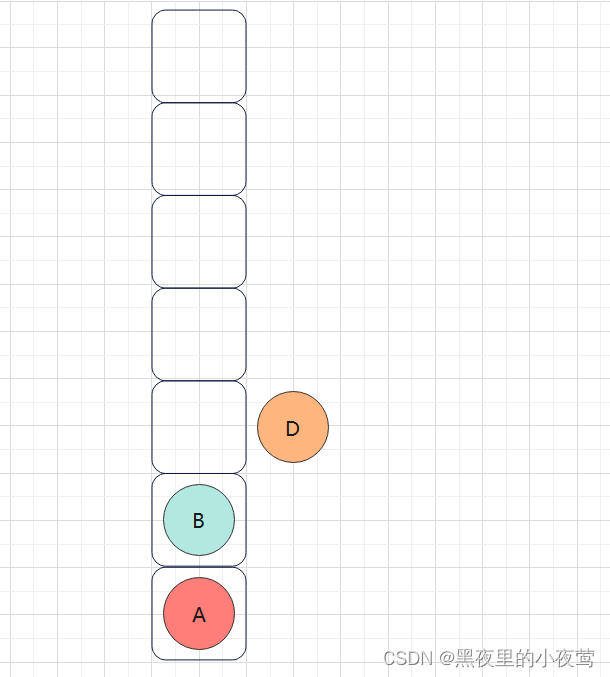
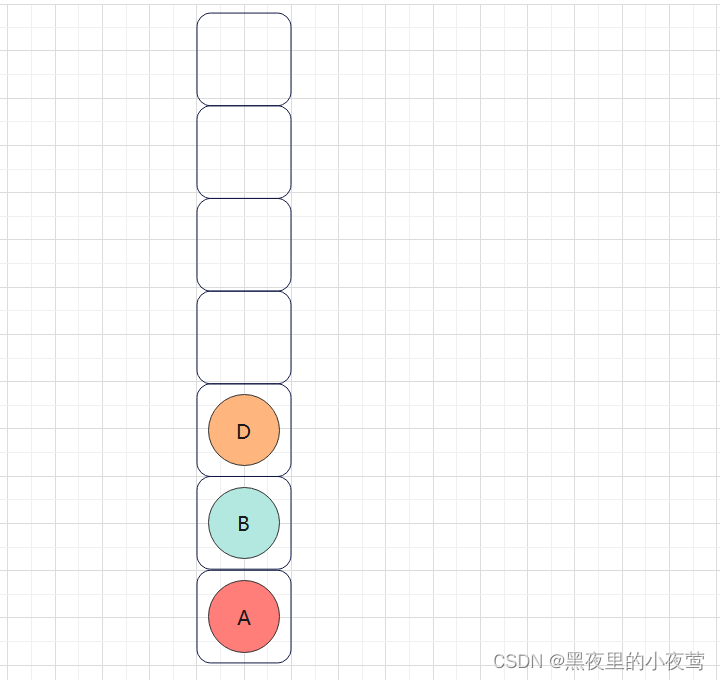
 但由于D的右子树为空，不遍历，故最后D出栈，并访问：

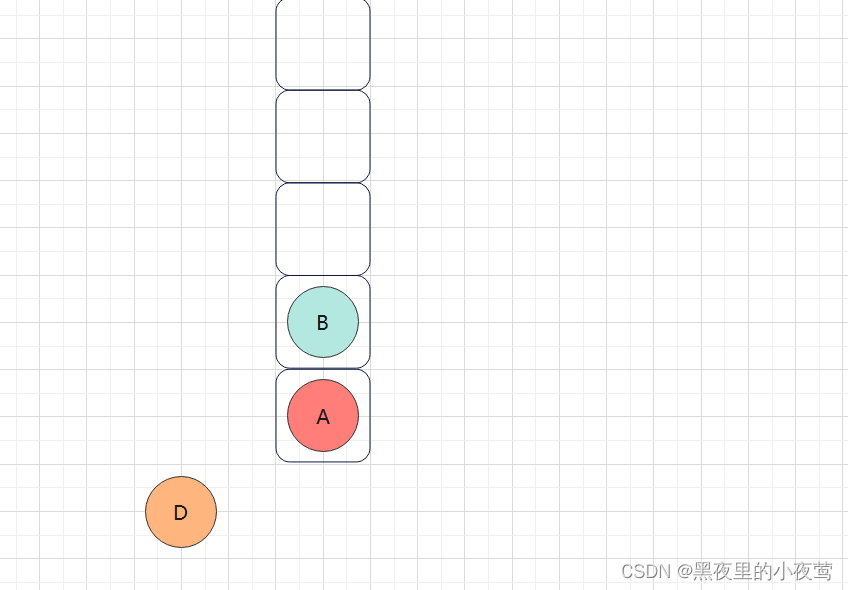
 至此D已经访问完（其左右子树也访问完），然后B出栈访问右子树，紧接着入栈，准备执行最后的出栈访问：

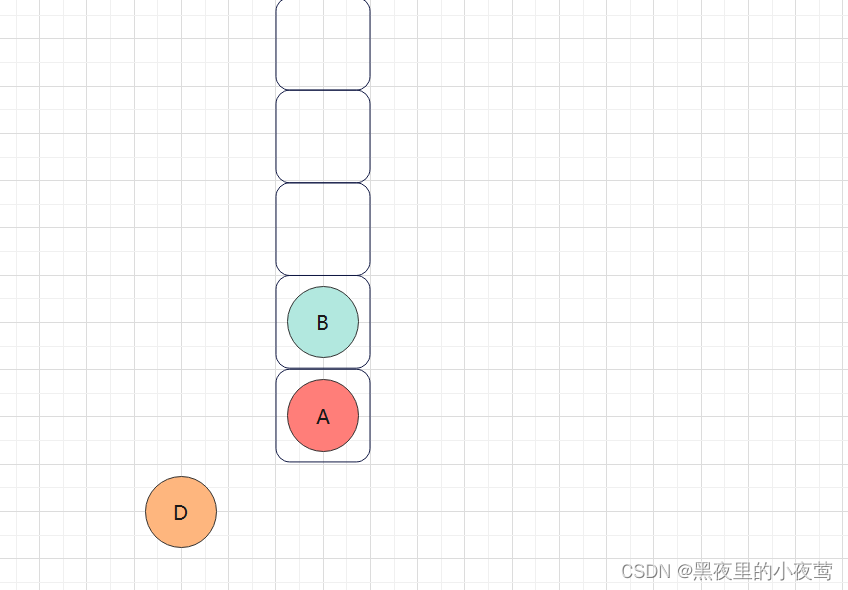
B的右子树不为空，E入栈，并遍历E的左子树：

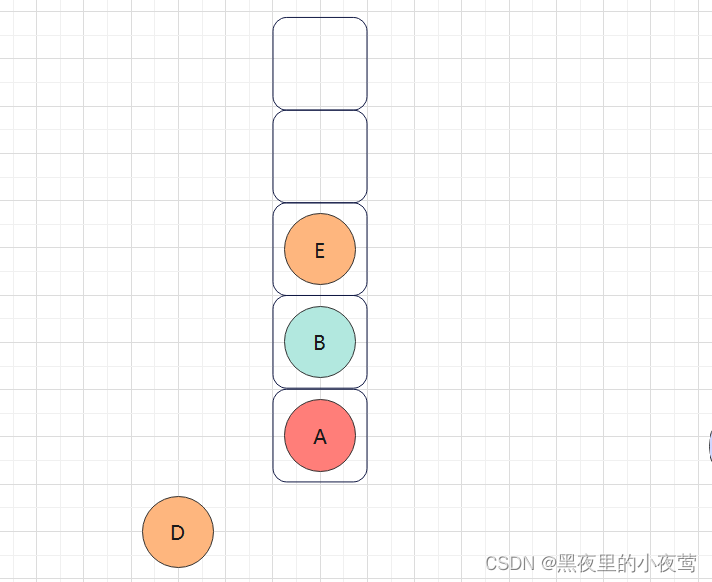
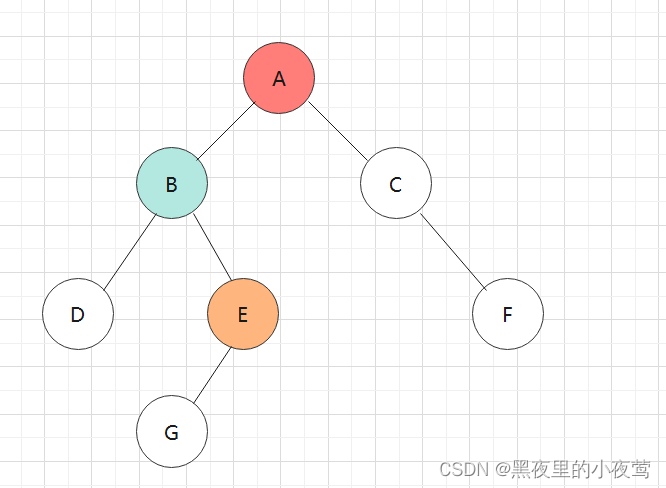
 E的左子树不为空，G入栈，并遍历G的左子树：

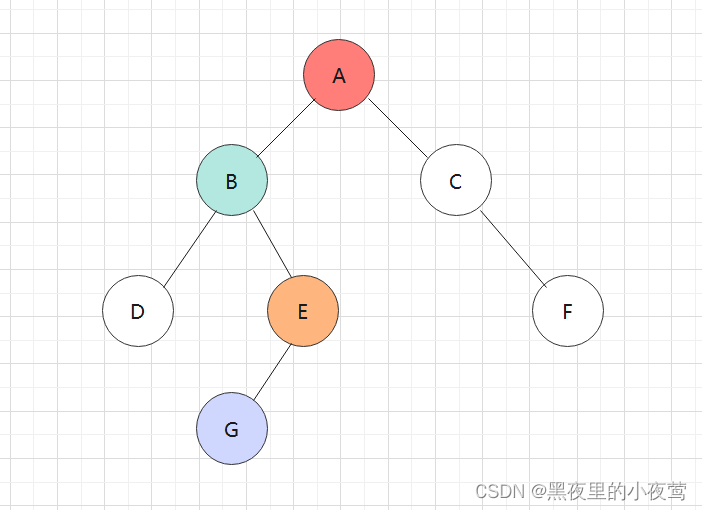
 G的左子树为空，不遍历，E出栈遍历右子树，紧接着入栈（此时还没访问G本身）：

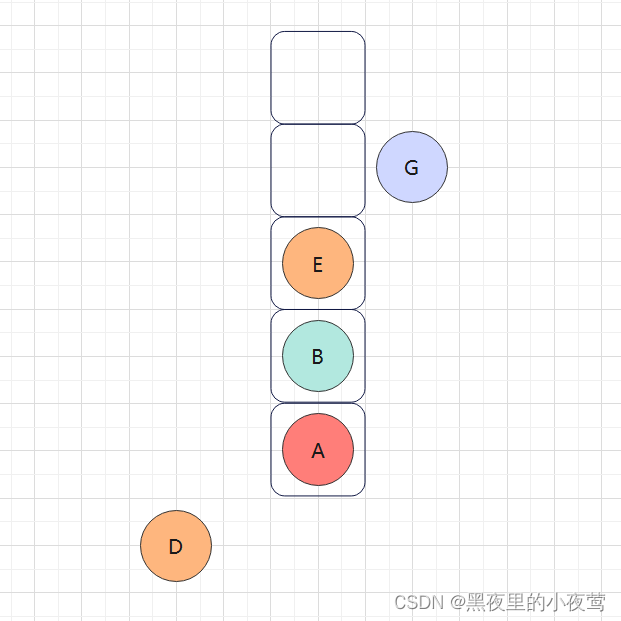
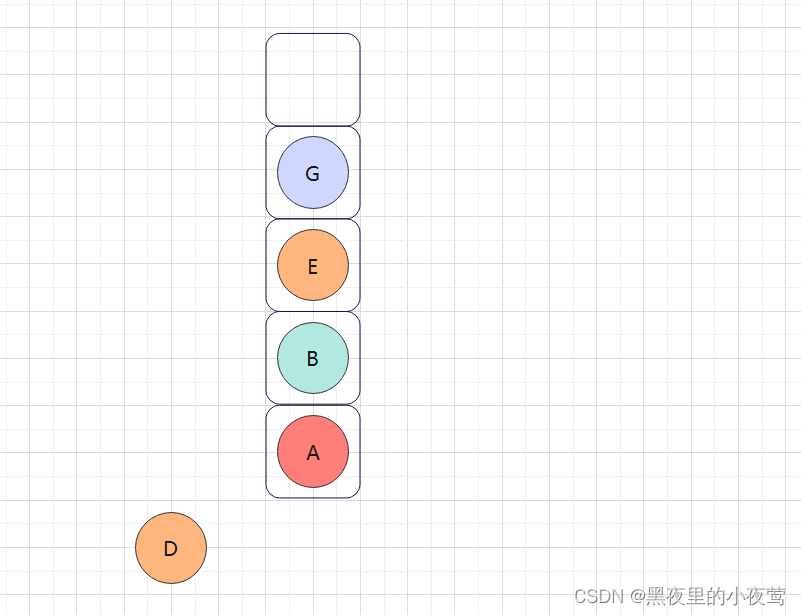
 G的右子树为空，不遍历，此时G的左右子树均遍历完，G出栈访问：

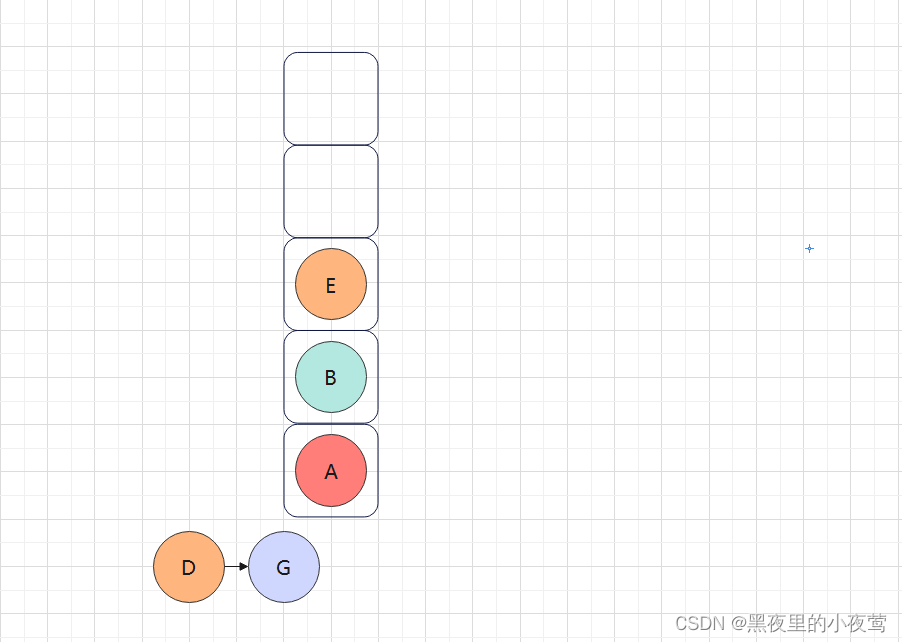
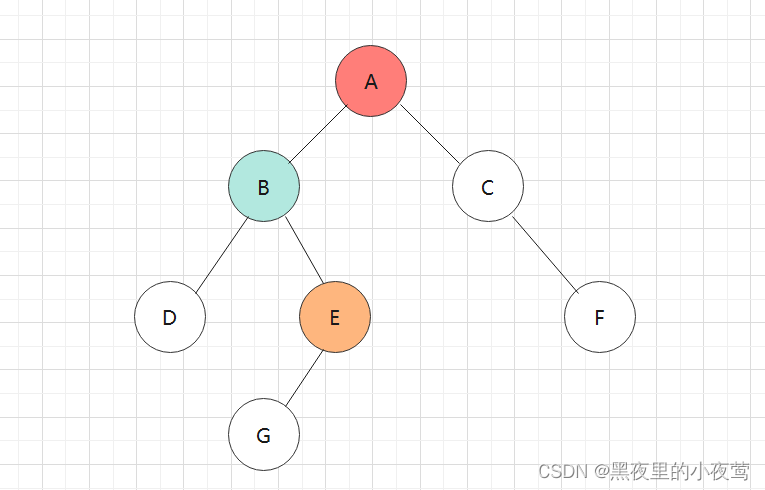
 接着E出栈遍历右子树，紧接着入栈，为后序的出栈访问自身做准备：

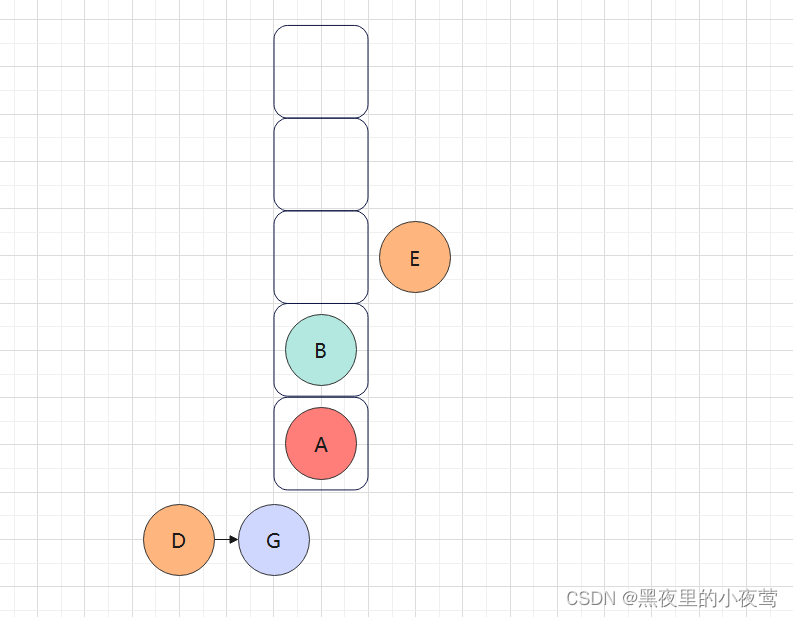
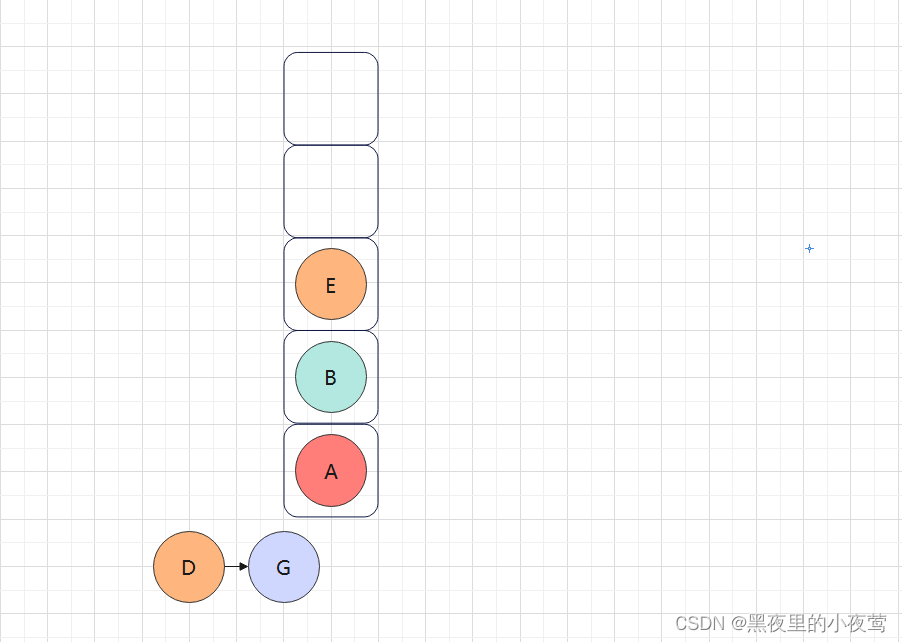
 E的右子树为空，不遍历，E的左右子树遍历完，E出栈访问：

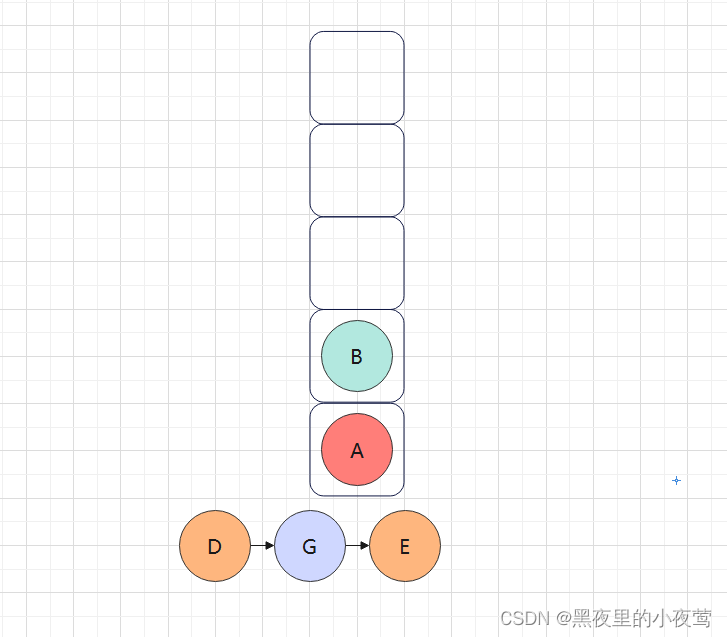
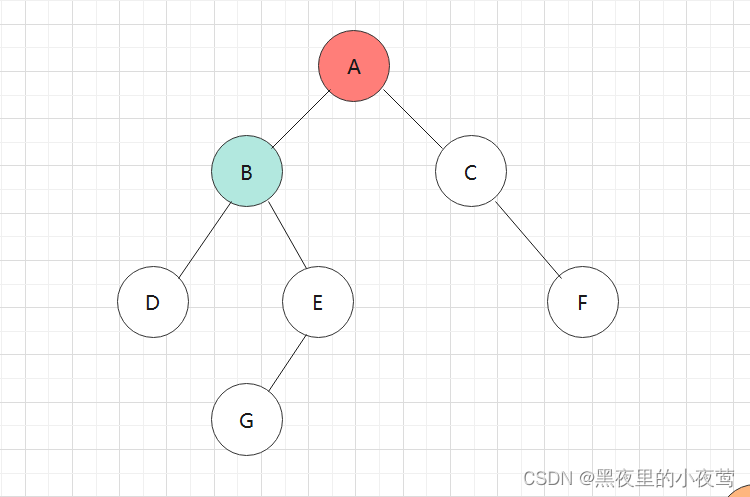
 此时B的左右子树已遍历完，B出栈访问：

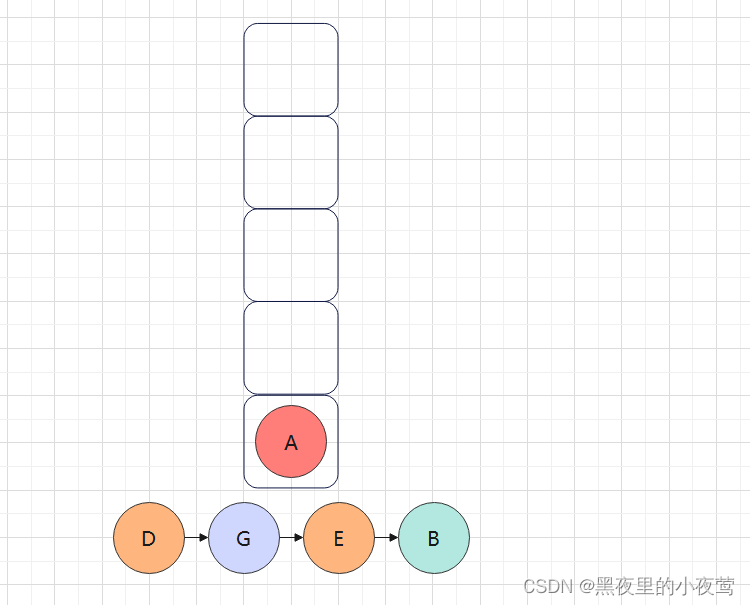
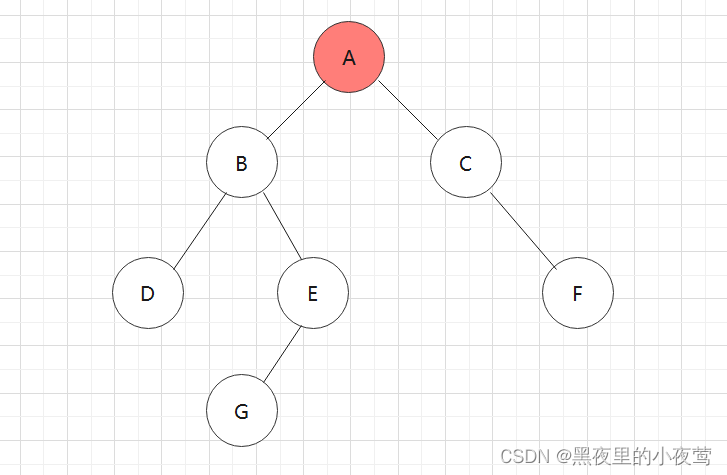
 B出栈后，此时栈中只剩下A，A出栈遍历右子树，紧接着入栈进行最后的出栈访问：

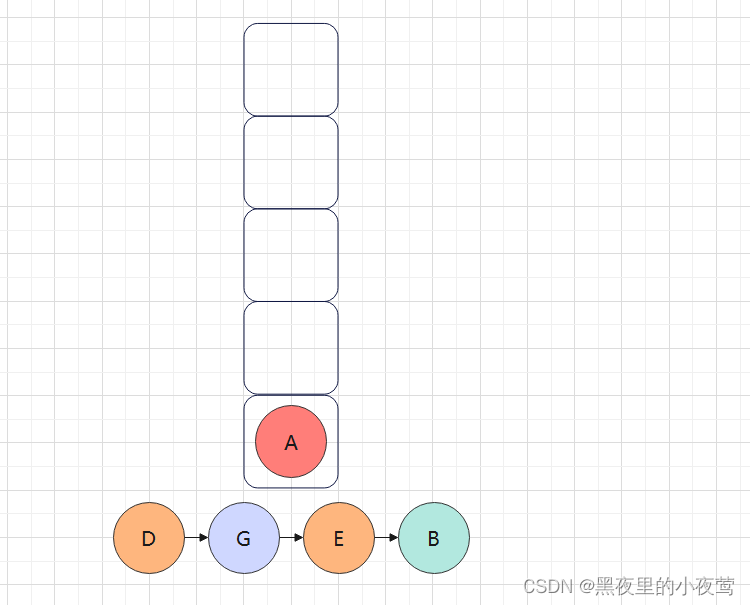
 A的右子树不为空，C入栈，遍历C的左子树：

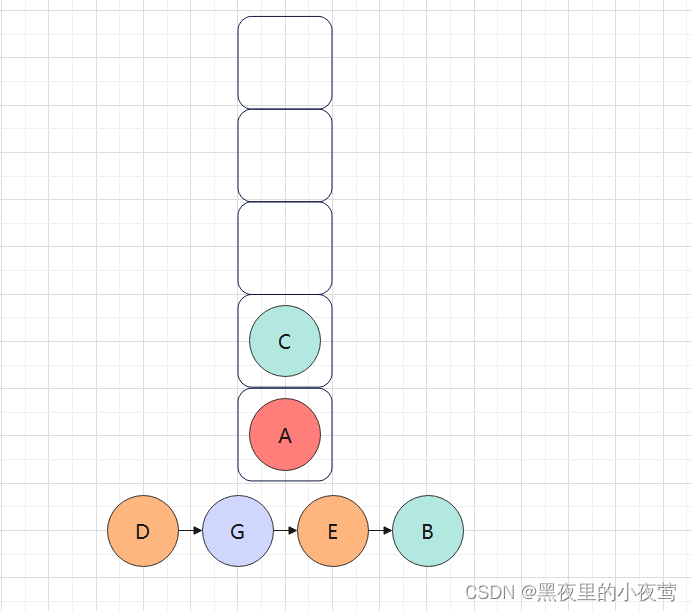
 C的左子树为空，不遍历，C出栈遍历其右子树，紧接着入栈做最后的出栈访问：

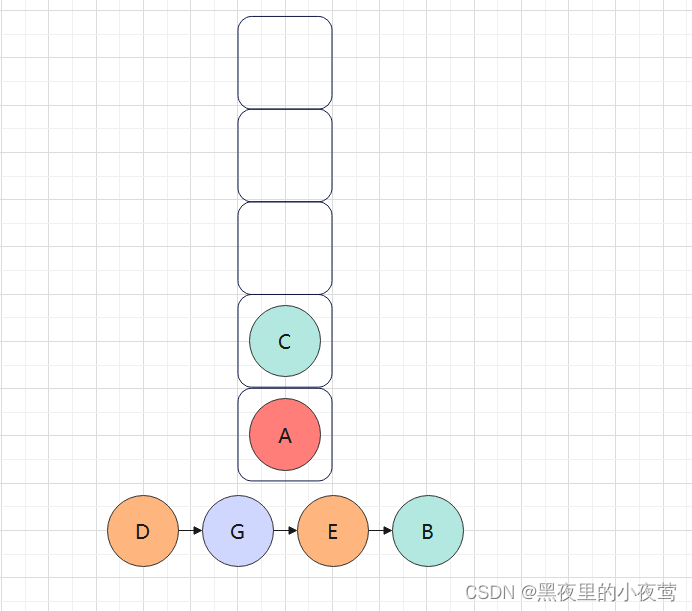
 C的右子树不为空，F入栈，遍历其左子树：

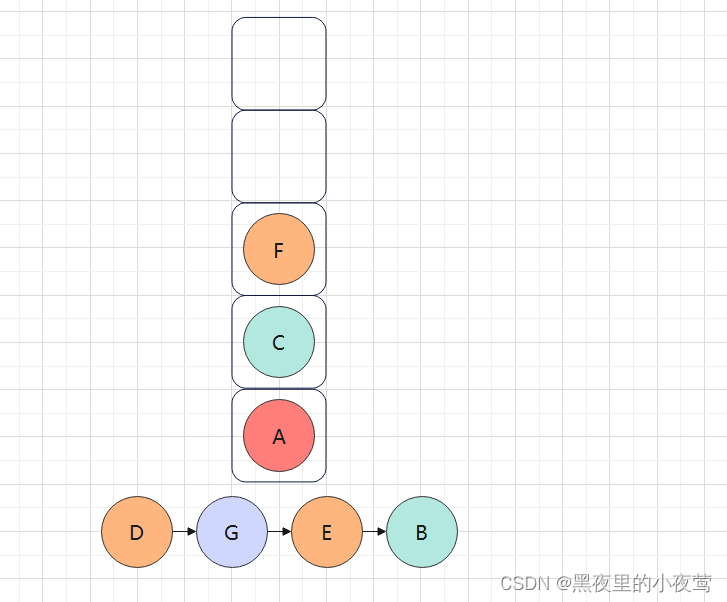
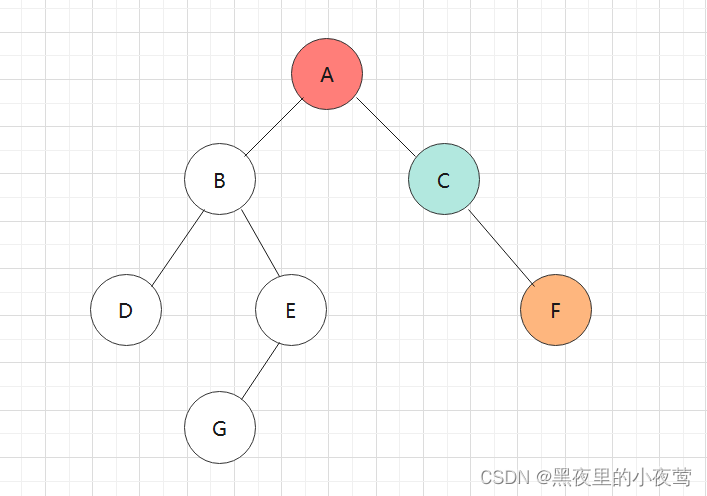
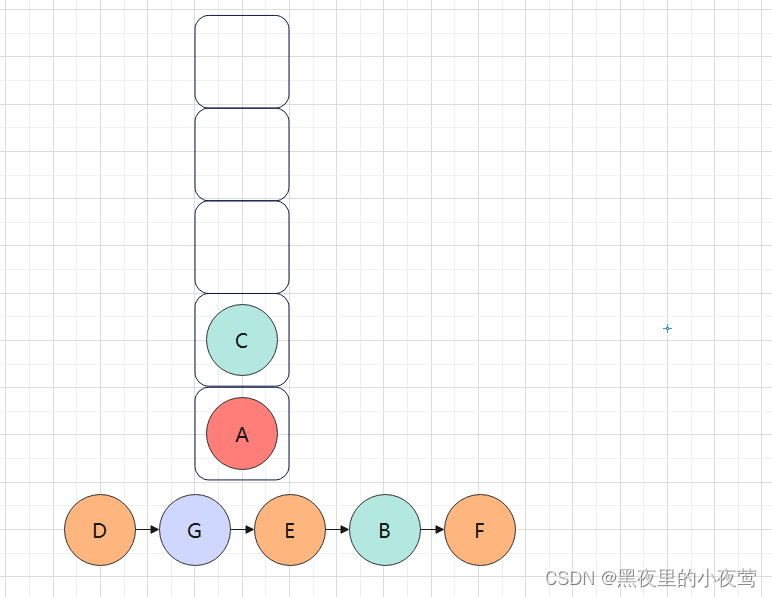
F的左子树为空，不遍历，F出栈遍历右子树，紧接着入栈做最后出栈访问，此时A、C、F均已做好最后出栈访问：

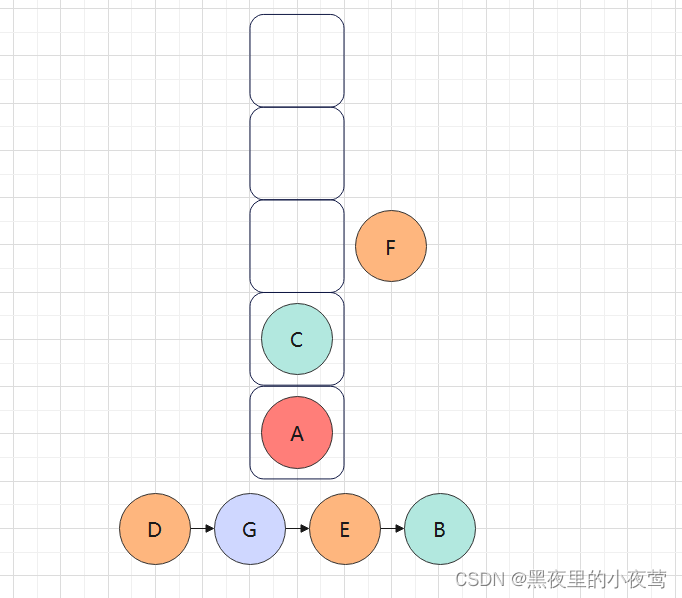
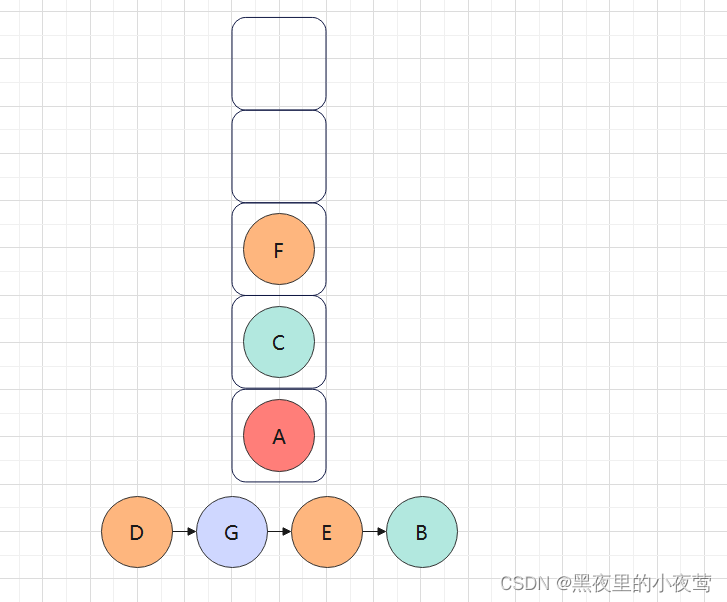
 F的右子树为空，不遍历，此时F的左右子树已遍历完，F出栈进行访问：

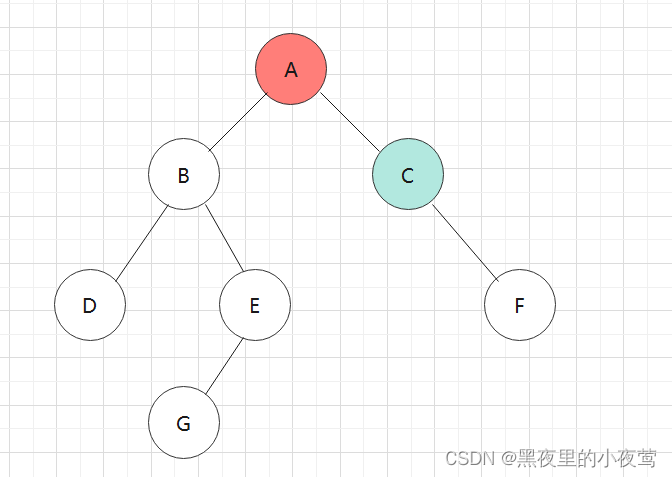
 C的左右子树已遍历完，C出栈访问：

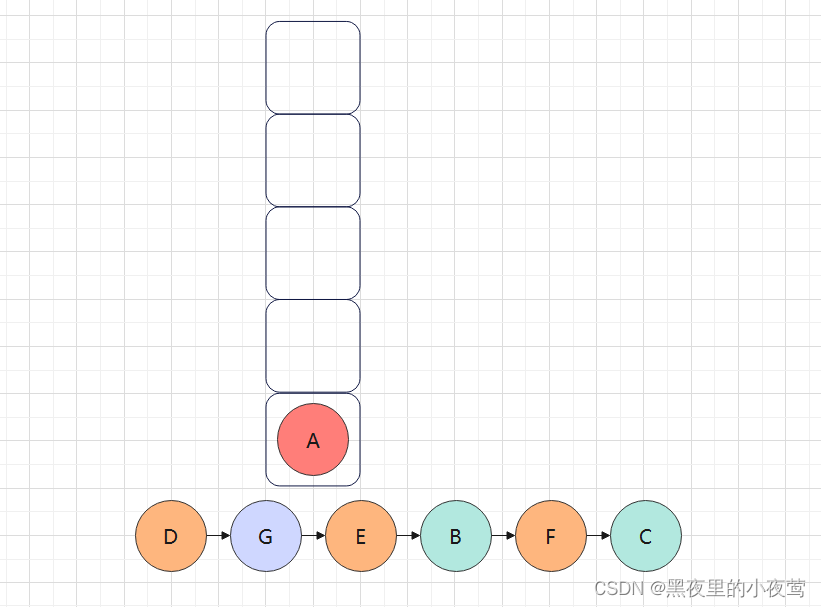
 此时栈中只剩A，A的左右子树已遍历完，A出栈访问：

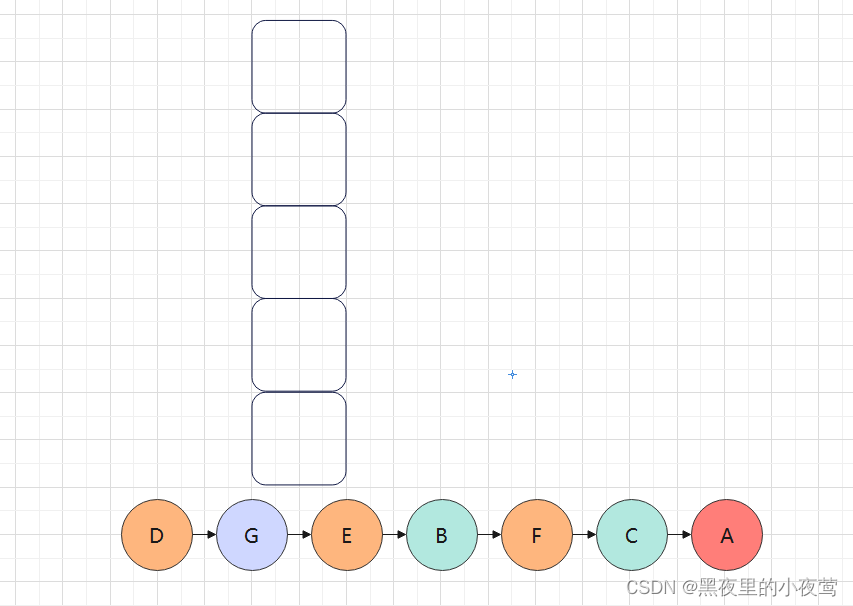
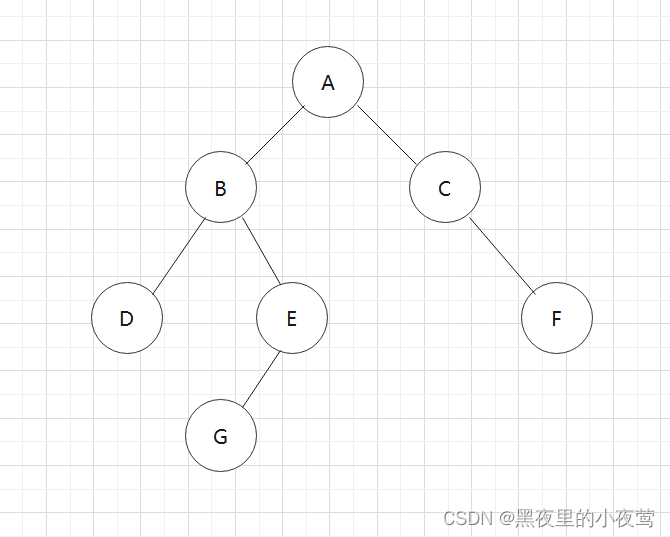
 遍历完成，每个结点有且仅有一次被访问，二叉树的后序遍历结果为：

（2）非递归版本

         后序遍历的非递归算法，也是和前面两种遍历算法一样，借用辅助栈，将递归函数隐式调用栈的过程给显示展示出来，但后序遍历非递归算法最需要解决的问题就是——上面的两次出栈问题（即判别哪次出栈是访问右子树，哪次出栈是访问自身），这是其利用辅助栈需要解决的事，而解决此事也有很多方法，这里介绍标志法，即设立一个标志来判别出栈。

算法思路：

1、当二叉树为空，则什么也不做；

2、结点不为空，入栈并设立标志 tag = 0，随后遍历左子树，；

3、结点为空，则判断栈是否为空，为空则遍历结束，不为空又分两种情况：

         i、tag = 1（说明栈顶元素的左右子树已遍历完），出栈访问栈顶元素（相当于上面的第二次出栈）。

         ii、栈顶标志tag，若tag = 0（说明栈顶元素的右子树还没遍历），则重新设置标志 tag = 1（此时还在栈中），并遍历栈顶元素的右子树（此过程相当于上面的第一次出栈，遍历右子树，紧接着入栈，故重新标志起到了说明右子树已访问过这个作用）；

算法实现：

/*后序遍历————利用标志*/
struct stack
{BiTree t;int tag;            // 标志
};						// tag = 0表示左子女被访问，tag = 1表示右字母被访问
void PostOrder3(BiTree T)
{struct stack s[Maxsize];int top = -1;while (T != NULL || top >= 0){while (T != NULL){s[++top].t = T;s[top].tag = 0;T = T->lchild;					// 沿左分支向下}while (top != -1 && s[top].tag == 1)visit(s[top--].t);					// 退栈if (top != -1){s[top].tag = 1;						// 标志访问过右子树被访问T = s[top].t->rchild;				// 沿右分支向下遍历}}
}

 算法图解：

依旧是熟悉的味道，咱们还是利用上面算法的那个二叉树：

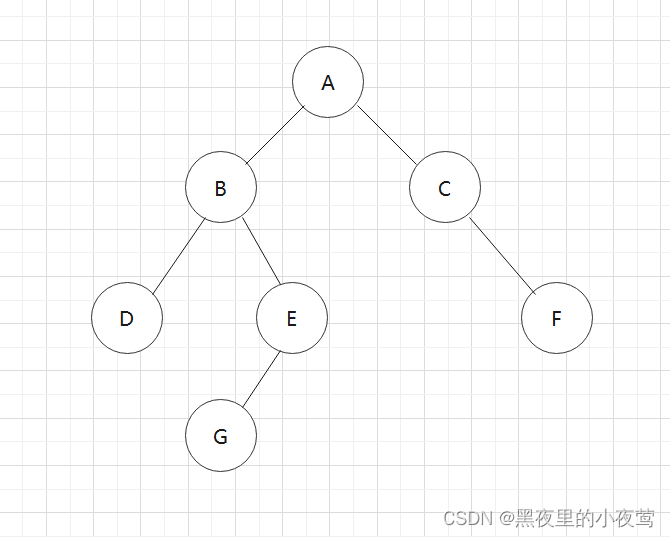
 首先T != NULL，A入栈，并设其标志 tag = 0，随后遍历A的左子树：

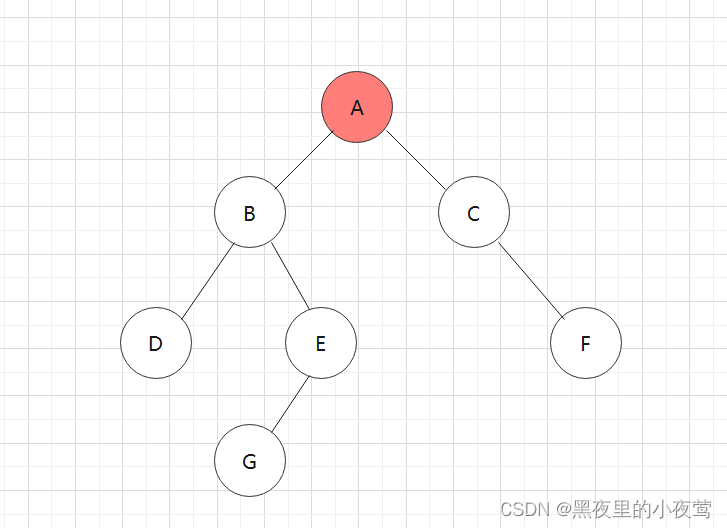
 A的左子树不为空，B入栈，并设其标志 tag = 0，接着遍历B的左子树：

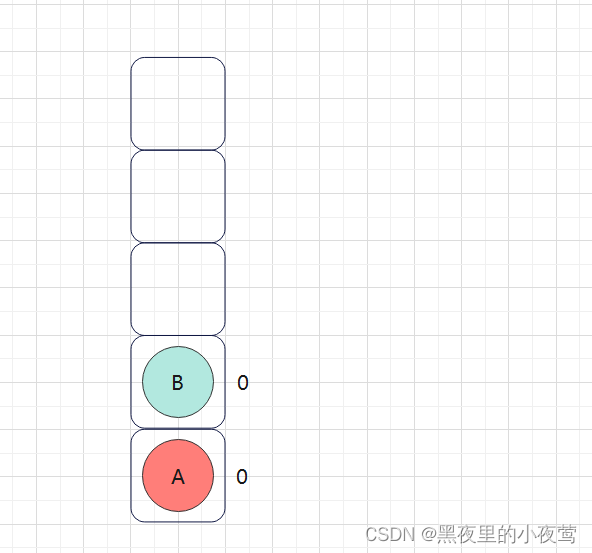
 B的左子树不为空，D入栈，并设其标志为 tag = 0，然后遍历D的左子树：

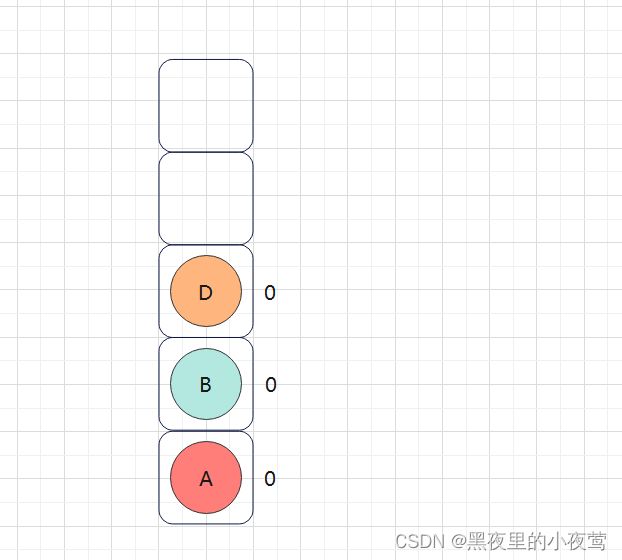
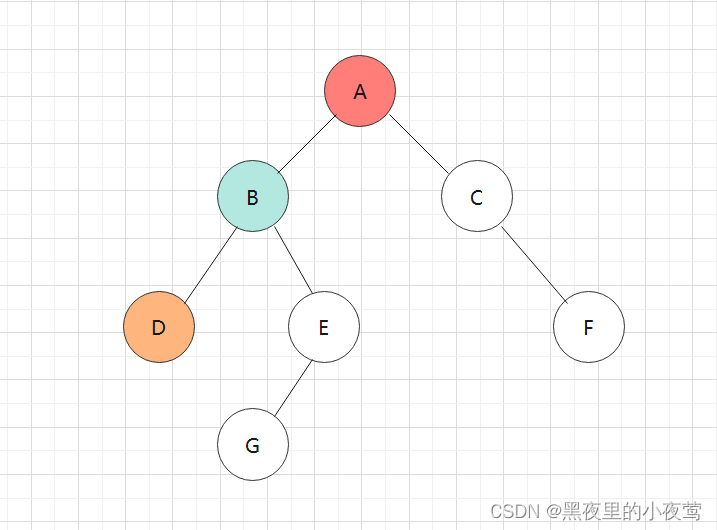
 D的左子树为空，不遍历，同时 tag = 0，说明D的右子树还没遍历，然后设置D的tag = 1，并遍历D的右子树（此时D还在栈中）：

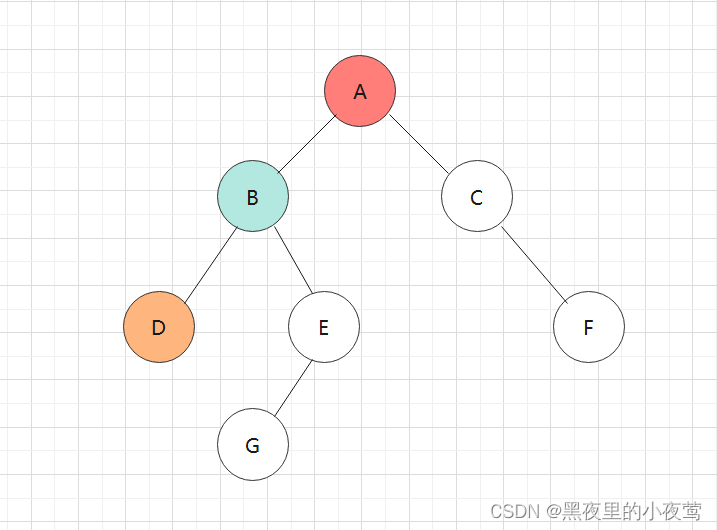
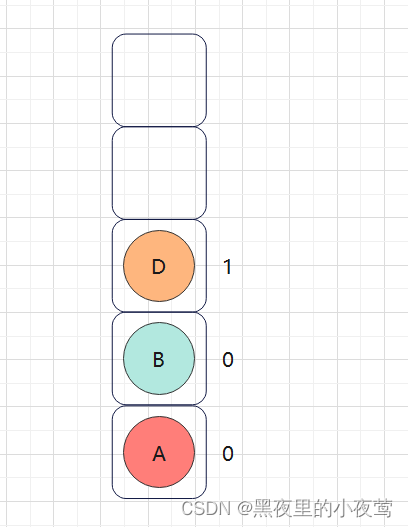
 D的右子树为空，不遍历，但由于tag = 1，故D出栈进行遍历：

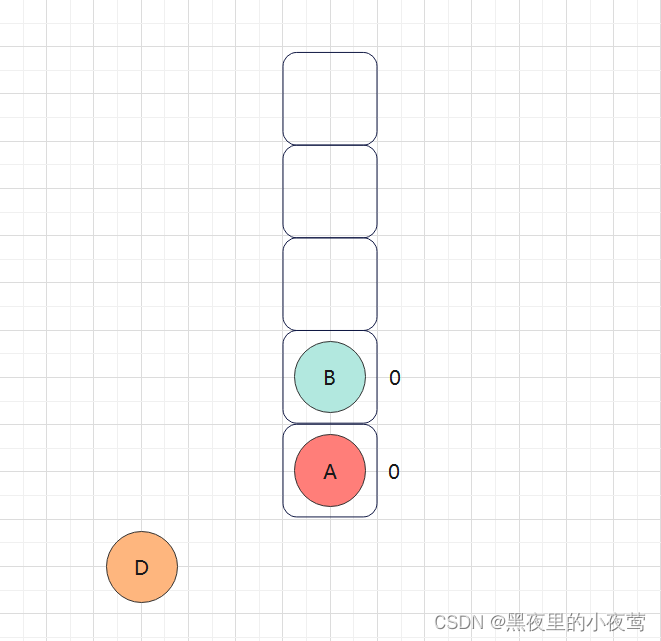
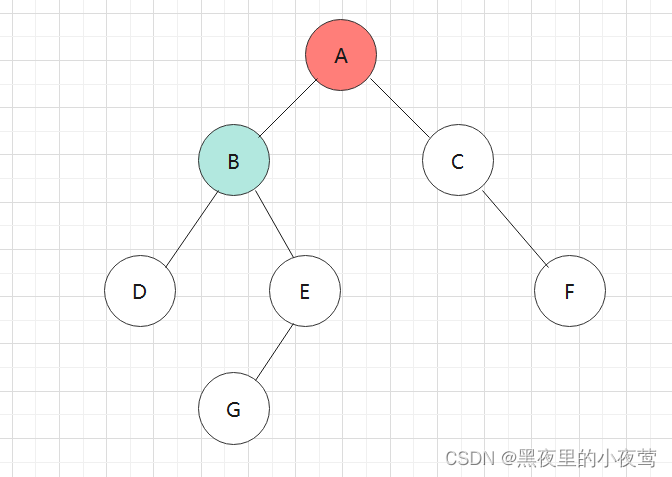
此时栈不为空， 然后栈顶元素B，tag = 0（其右子树没遍历过）故不出栈访问，重新设置 tag = 1，并遍历B的右子树：

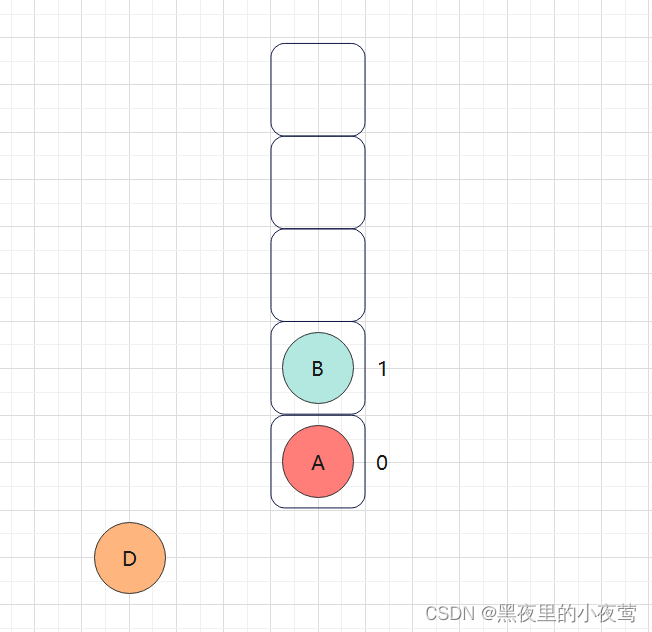
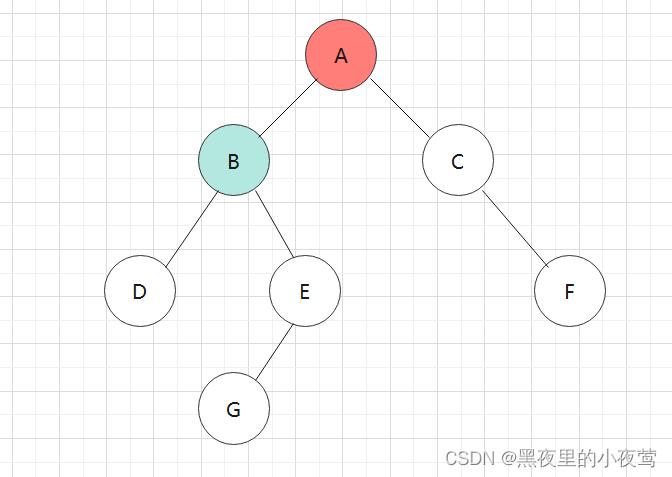
 B的右子树不为空，E入栈并设置tag = 0，随后遍历其左子树：

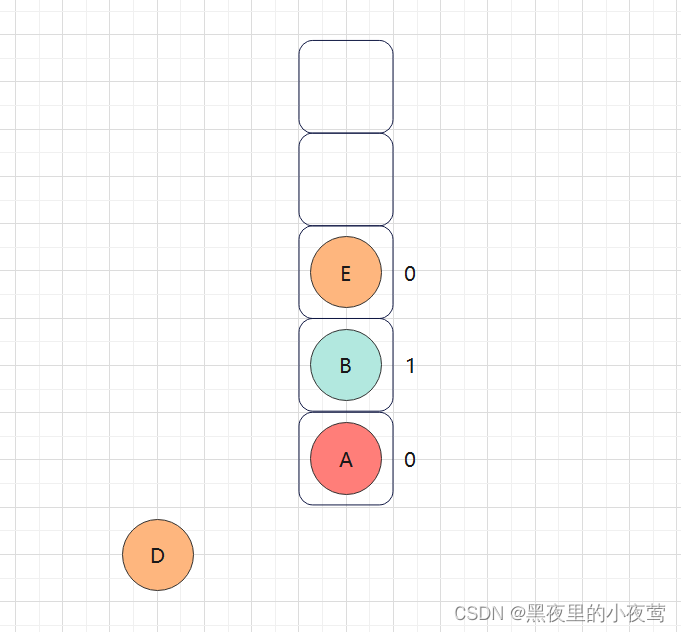
E的左子树不为空，G入栈并设立tag = 0，接着遍历G的左子树：

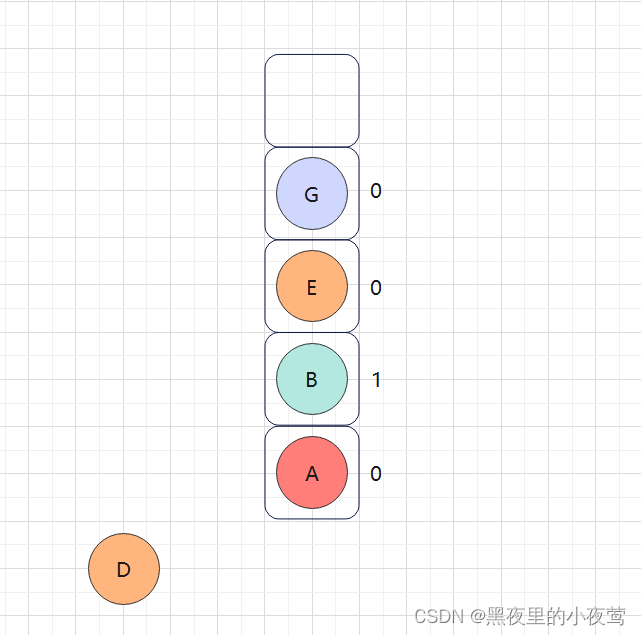
 G的左子树为空，不遍历，但tag = 0，故重新设置tag = 1，并遍历G的右子树：

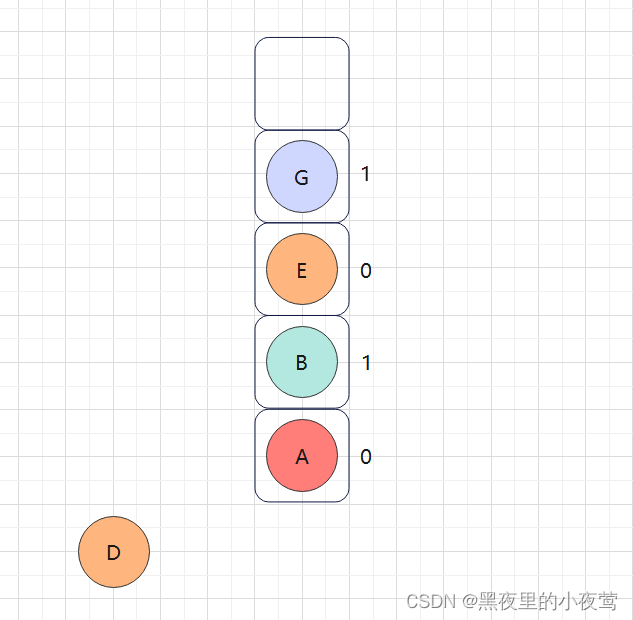
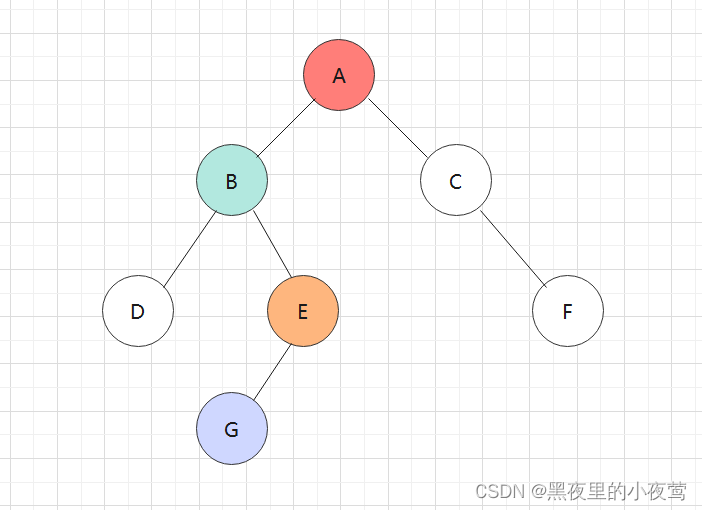
 G的右子树也为空，不遍历，由于此时G的tag = 1（说明G的左右子树已遍历完），G出栈访问：

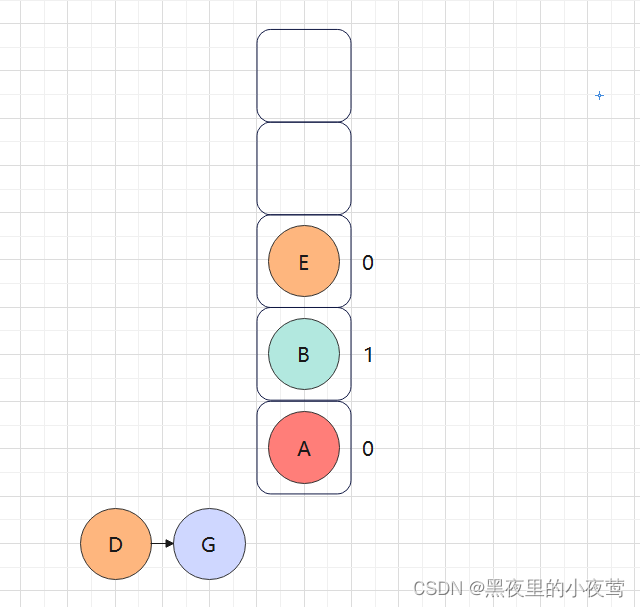
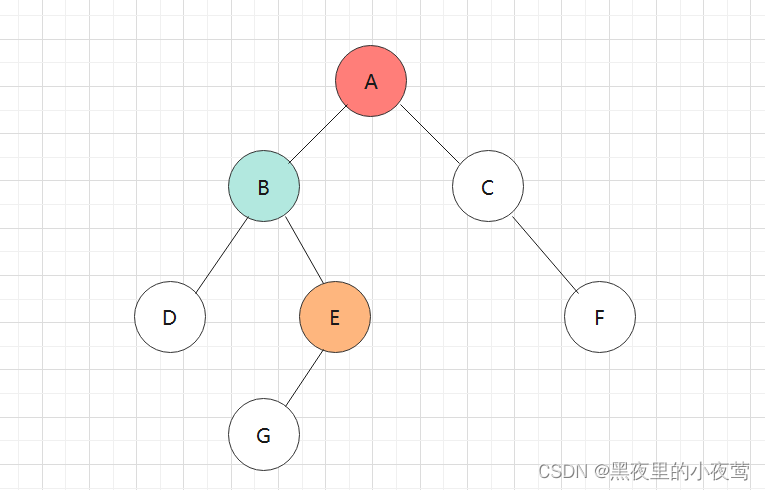
 此时由于E的tag = 0，不出栈访问并重新设置tag = 1，遍历E的右子树：

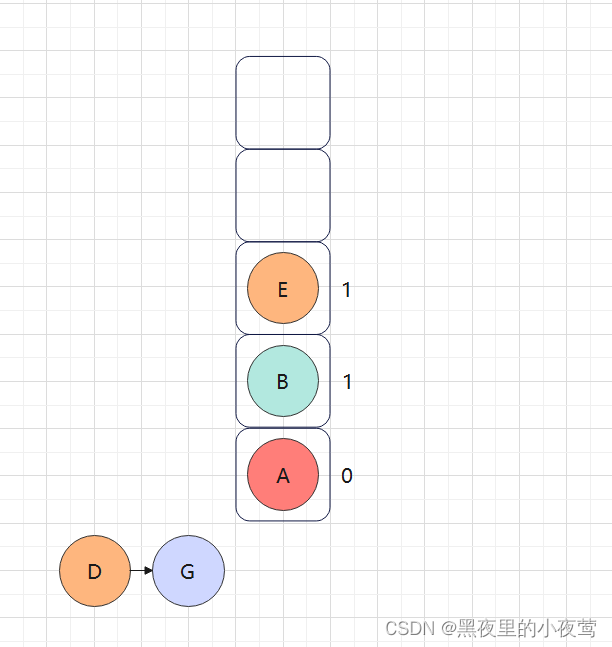
 E的右子树为空，不遍历，并且此时tag = 1，故E出栈并访问：

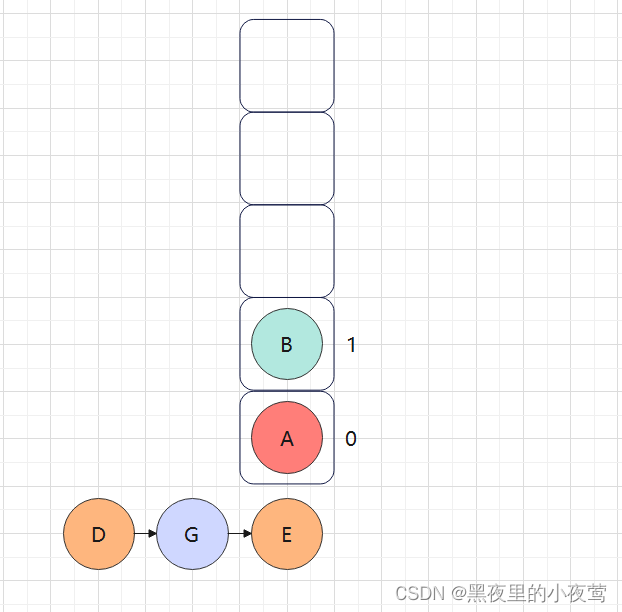
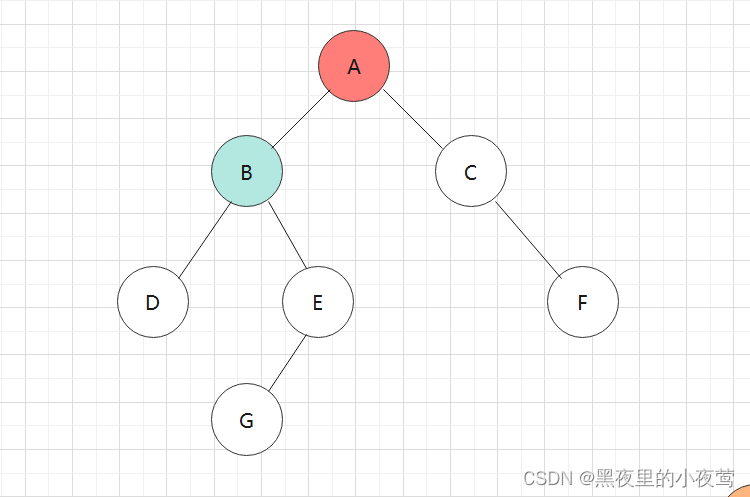
 此时由于栈顶元素B的tag = 1，故B也出栈访问：

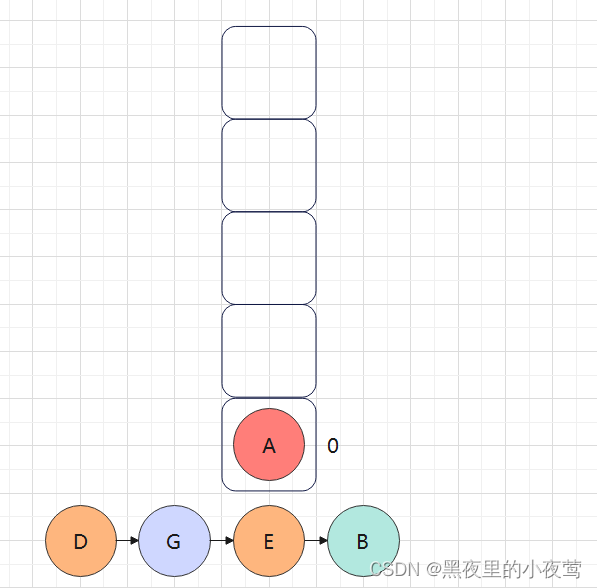
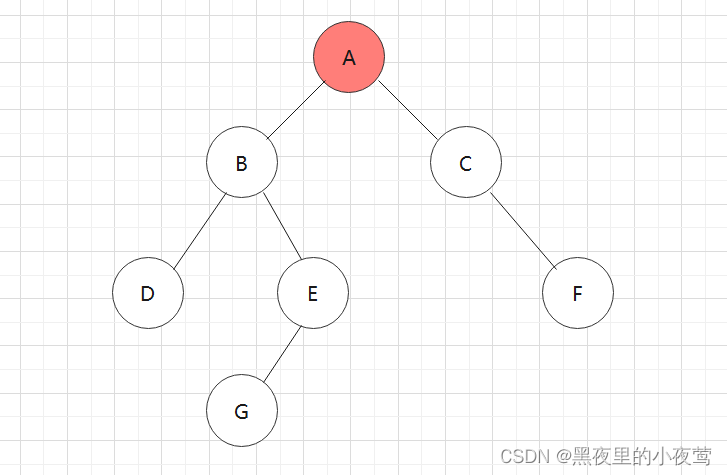
 紧接着，A的tag = 0，故其不被访问，并重新设置tag = 1，遍历A的右子树：

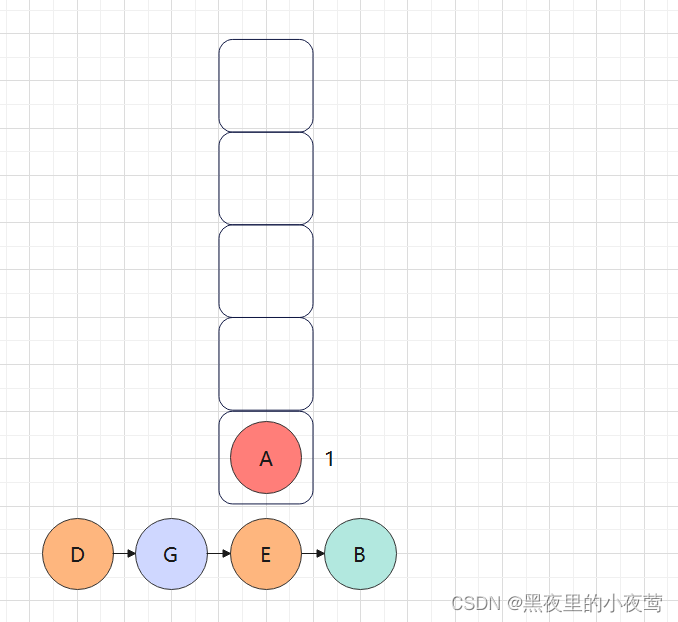
 A的右子树不为空，C入栈，并设置tag = 0，遍历C的左子树：

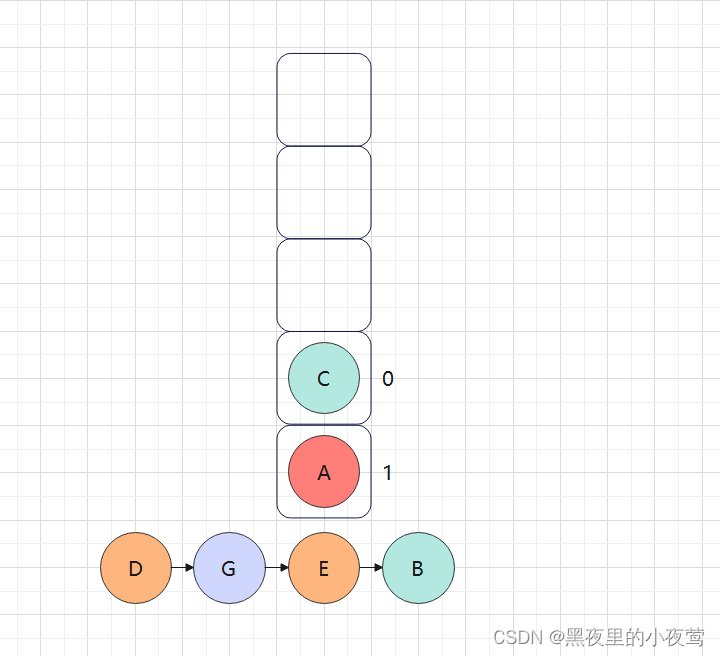
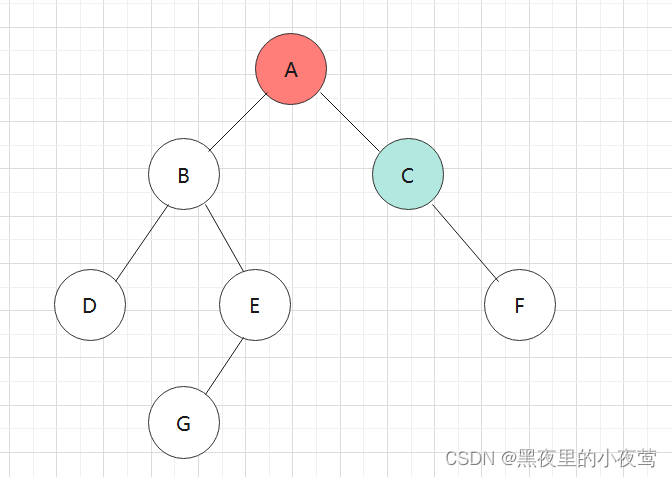
 C的左子树为空，不遍历，由于此时C的tag = 0，故重新设置 tag = 1，遍历C的右子树：

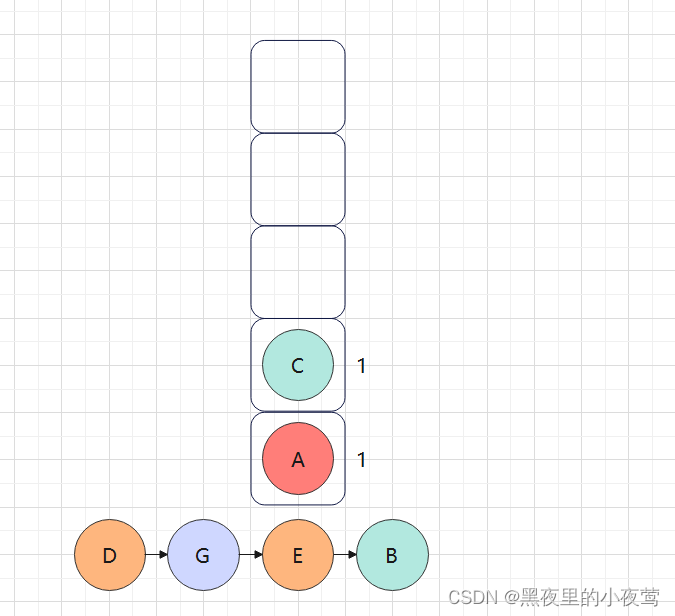
 C的右子树不为空，F入栈并令其标志tag = 0，遍历其左子树：

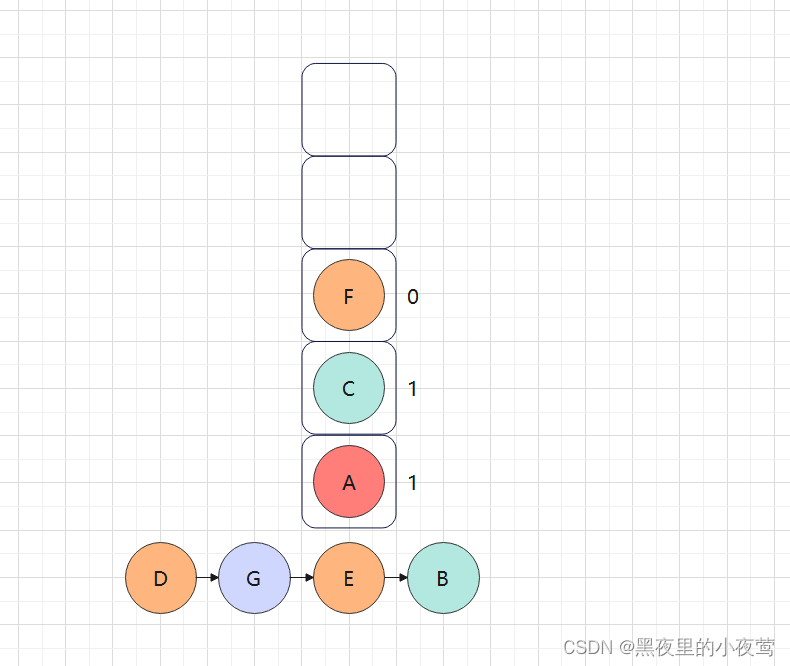
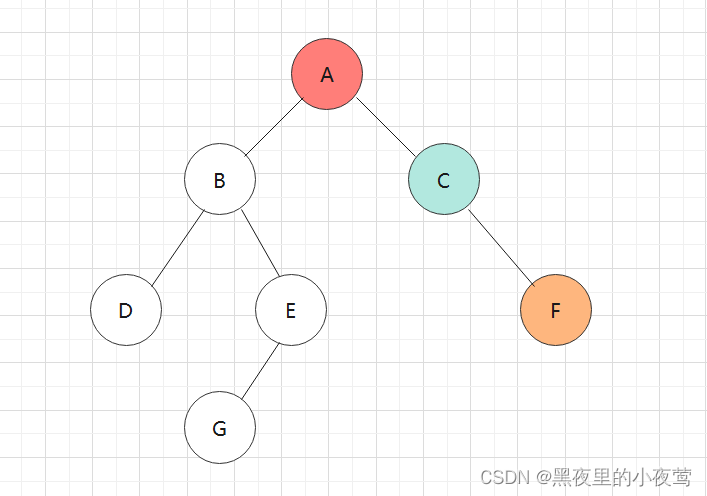
 F的左子树为空，不遍历，由于此时tag = 0，故重新设置tag = 1，遍历其右子树：

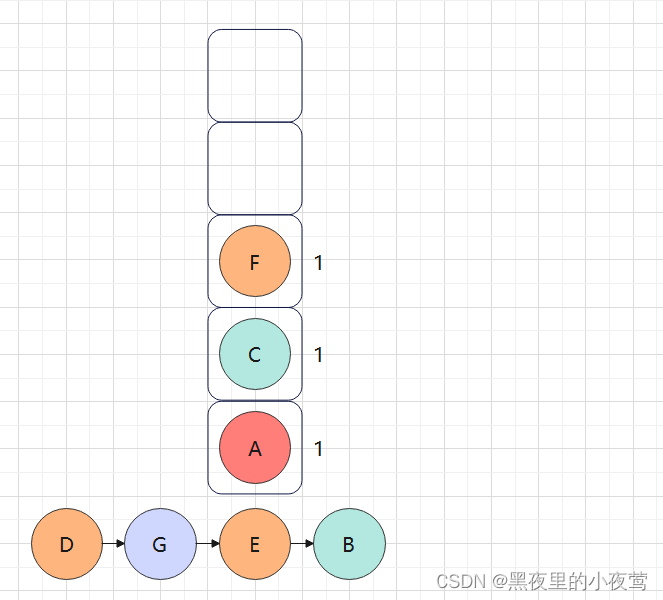
 F的右子树也为空，但此时tag = 1，故F出栈访问：

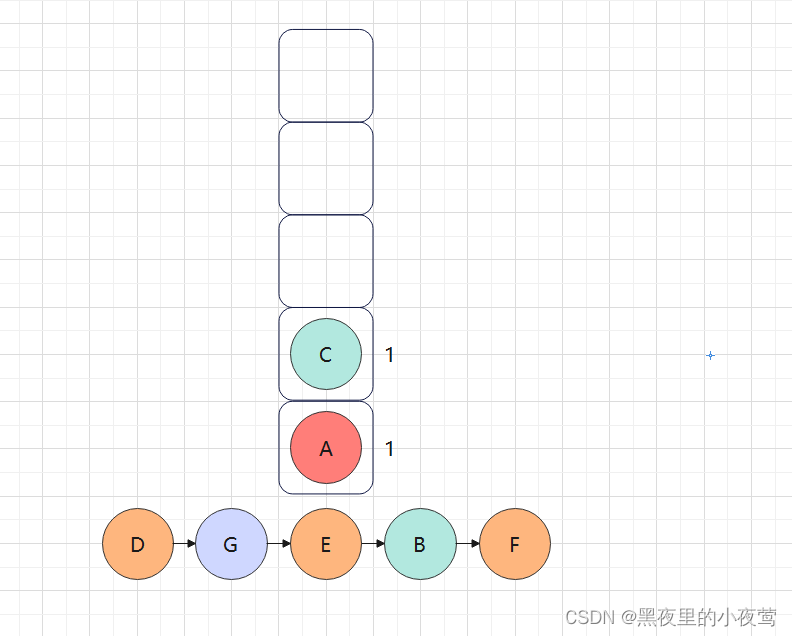
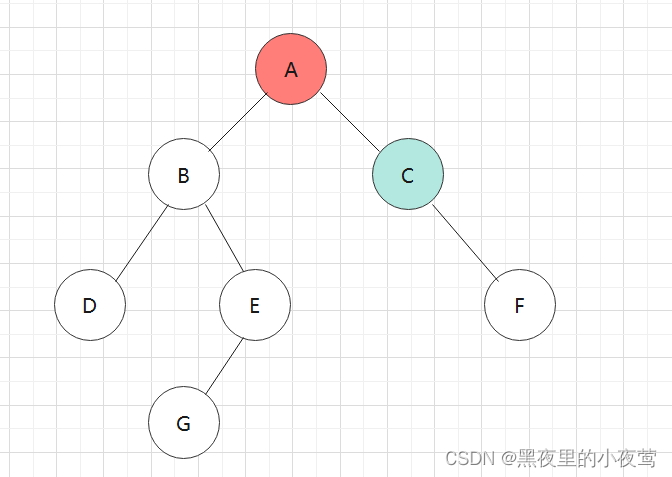
 此时由于栈顶元素C的tag = 1，故其也出栈访问：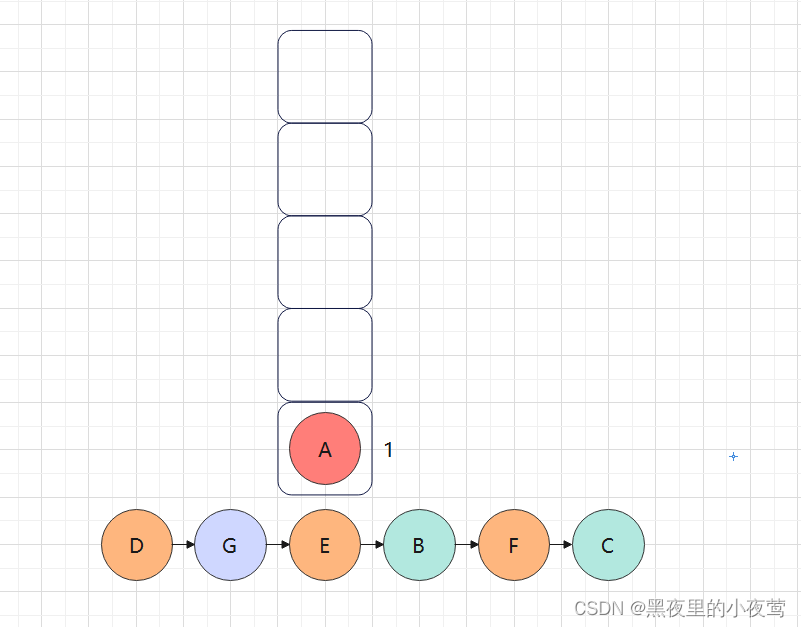

 A的tag也为1，故其也出栈访问：

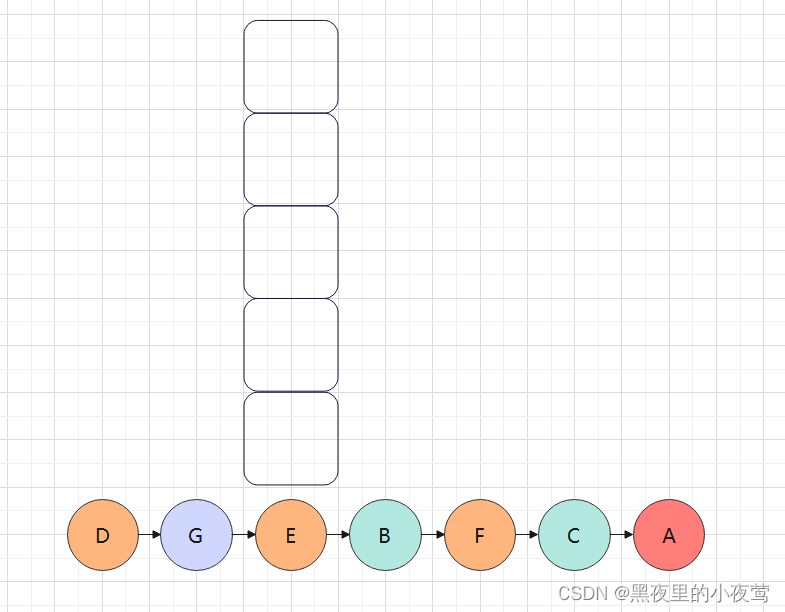
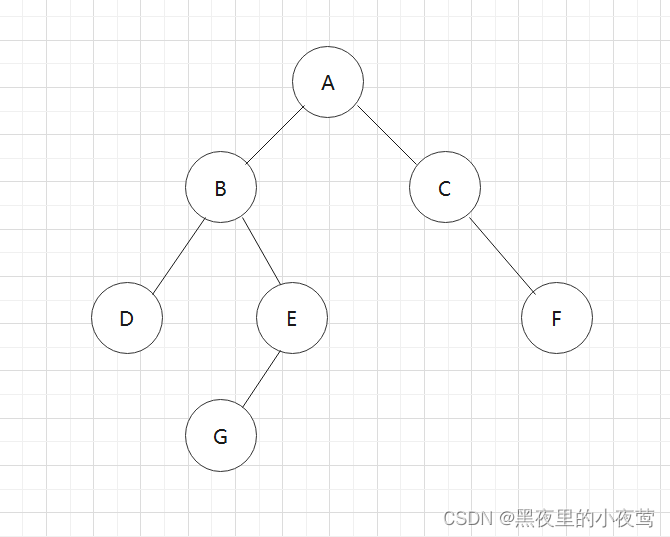
 此时栈为空，结点也为空，结束遍历，最后上面这颗二叉树的后序遍历结果为：

 同上面的后序遍历递归算法的结果一致。

四、总结

        二叉树的前、中、后序遍历的递归算法只是访问根结点的时间不同，但是都是先访问左子树再访问右子树，故如果去掉访问根结点这个步骤的话（即visit(T)）,这三种算法遍历的结点顺序一致，并且递归算法利用到调用栈，这是隐式的调用，我们的非递归算法就是把这个隐式调用的过程给真实显示出来。

五、测试程序

/*请输入：ABD##EG###C#F## */
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <windows.h>#define Maxsize 100  // 定义栈中元素的最大个数typedef char Elemtype;  // 数据类型/*二叉树的链式存储结构*/
typedef struct BiTNode
{Elemtype data; // 数据域struct BiTNode* lchild, * rchild; // 左右孩子指针
}BiTNode, * BiTree;/*栈的存储结构*/
typedef struct Stack
{BiTree data[Maxsize]; // 存放栈中元素int top;		// 栈顶指针
}SqStack;/*设置字体颜色*/
void color(short x);/*测试菜单*/
int TestMeanu(void);/*初始化栈*/
void InitStack(SqStack* S);
/*判断栈空*/
bool IsEmpty(SqStack S);
/*入栈*/
bool Push(SqStack* S, BiTree x);
/*出栈*/
bool Pop(SqStack* S, BiTree* x);/*创建二叉树*/
/*利用一个前序遍历的扩展二叉树的字符串序列*/
void CreateBiTree1(BiTree* T);/*二叉树遍历的递归算法*/
/*先序遍历*/
void PreOrder(BiTree T);
/*中序遍历*/
void InOrder(BiTree T);
/*后序遍历*/
void PostOrder(BiTree T);/*输出树结点*/
void visit(BiTree T);/*二叉树遍历的非递归算法*/
/*先序遍历*/
void PreOrder2(BiTree T);
/*中序遍历*/
void InOrder2(BiTree T);
/*后序遍历*/
/*利用标志*/
void PostOrder3(BiTree T);int main(void)
{BiTree T = NULL;printf("请输入以下字符串创建二叉树！！！\n");printf("ABD##EG###C#F##\n");CreateBiTree1(&T);while (true){	int choice = TestMeanu();switch (choice){case 0:exit(0);break;case 1:printf("1、先序遍历\n");printf("2、中序遍历\n");printf("3、后序遍历\n");printf("请输入要遍历的方式：");int choice1;scanf("%d", &choice1);color(11);switch (choice1){case 1:PreOrder(T);break;case 2:InOrder(T);break;case 3:PostOrder(T);break;default:printf("输入不规范，请规范输入！！！！\n");}break;case 2:printf("1、先序遍历\n");printf("2、中序遍历\n");printf("3、后序遍历\n");printf("请输入要遍历的方式：");int choice2;scanf("%d", &choice2);color(11);switch (choice2){case 1:PreOrder2(T);break;case 2:InOrder2(T);break;case 3:PostOrder3(T);break;default:printf("输入不规范，请规范输入！！！！\n");}}}
}/*设置字体颜色*/
void color(short x)
{/*颜色函数SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE),前景色 | 背景色 | 前景加强 | 背景加强);前景色：数字0-15 或 FOREGROUND_XXX 表示	（其中XXX可用BLUE、RED、GREEN表示）前景加强：数字8 或 FOREGROUND_INTENSITY 表示背景色：数字16 32 64 或 BACKGROUND_XXX 三种颜色表示背景加强： 数字128 或 BACKGROUND_INTENSITY 表示主要应用：改变指定区域字体与背景的颜色前景颜色对应值：0=黑色                8=灰色　　1=蓝色                9=淡蓝色        十六进制        　　2=绿色                10=淡绿色       0xa        　　3=湖蓝色              11=淡浅绿色      0xb　4=红色                12=淡红色       0xc　　5=紫色                13=淡紫色       0xd        　　6=黄色                14=淡黄色       0xe        　　7=白色                15=亮白色       0xf也可以把这些值设置成常量。*/if (x >= 0 && x <= 15)//参数在0-15的范围颜色SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), x);	//只有一个参数，改变字体颜色 else//默认的颜色白色SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), 7);
}/*测试菜单*/
int TestMeanu(void)
{color(16);int choice;printf("欢迎使用二叉树三种遍历算法测试程序!!!!!\n");printf("0、退出测试程序\n");printf("1、二叉树的递归遍历算法\n");printf("2、二叉树的非递归遍历算法\n");printf("请输入你需要测试的功能：");scanf("%d", &choice);return choice;
}/*初始化栈*/
void InitStack(SqStack* S)
{S->top = -1;
}/*判断栈空*/
bool IsEmpty(SqStack S)
{if (S.top == -1)return true;elsereturn false;
}/*入栈*/
bool Push(SqStack* S, BiTree x)
{if (S->top == Maxsize - 1)   // 栈满return false;S->data[++(S->top)] = x;return true;
}/*出栈*/
bool Pop(SqStack* S, BiTree* x)
{if (S->top == -1) // 栈空return false;*x = S->data[(S->top)--];return true;
}/*二叉树遍历的递归算法*/
/*先序遍历*/
void PreOrder(BiTree T)
{if (T != NULL){visit(T);				// 访问结点PreOrder(T->lchild);	// 遍历结点左子树PreOrder(T->rchild);	// 遍历结点右子树}
}/*中序遍历*/
void InOrder(BiTree T)
{if (T != NULL){InOrder(T->lchild);		// 遍历结点左子树visit(T);				// 访问结点InOrder(T->rchild);		// 遍历结点右子树}
}/*后序遍历*/
void PostOrder(BiTree T)
{if (T != NULL){PostOrder(T->lchild);	// 遍历结点左子树PostOrder(T->rchild);	// 遍历结点右子树visit(T);				// 访问结点}
}/*二叉树的非递归算法*/
/*先序遍历*/
void PreOrder2(BiTree T)
{SqStack S;				  // 申请一个辅助栈InitStack(&S);			  // 初始化BiTree p = T;			  // p为遍历指针while (p || !IsEmpty(S))  // 栈不为空或p不为空时循环{if (p)			      // 一路向左{visit(p);		  // 访问当前节点，并入栈Push(&S, p);p = p->lchild;	  // 左孩子不空，一直向左走}else				  //出栈，并转向出栈结点的右子树{Pop(&S, &p);	  // 栈顶元素出栈p = p->rchild;    // 向右子树走，p赋值为当前结点的右孩子}					  // 返回while循环继续进入if-else语句}
}/*中序遍历*/
void InOrder2(BiTree T)
{SqStack S;                  // 申请一个辅助栈InitStack(&S);				// 初始化BiTree p = T;				// p为遍历指针while (p || !IsEmpty(S))    // 栈不空或p不空时循环{if (p)					// 一路向左{Push(&S, p);        // 当前结点入栈p = p->lchild;		// 左孩子不空，一直向左走}else					// 出栈，并转向出栈结点的右子树{Pop(&S, &p);		// 栈顶元素出栈visit(p);			// 访问出栈结点p = p->rchild;		// 向右子树走，p赋值为当前结点的右孩子}						// 返回while循环继续进入if-else语句}
}/*利用标志*/
struct stack
{BiTree t;int tag;			// 标志
};						// tag = 0表示左子女被访问，tag = 1表示右字母被访问
void PostOrder3(BiTree T)
{struct stack s[Maxsize];int top = -1;while (T != NULL || top >= 0){while (T != NULL){s[++top].t = T;s[top].tag = 0;T = T->lchild;					// 沿左分支向下}while (top != -1 && s[top].tag == 1)visit(s[top--].t);					// 退栈if (top != -1){s[top].tag = 1;						// 标志访问过右子树被访问T = s[top].t->rchild;				// 沿右分支向下遍历}}
}/*输出树结点*/
void visit(BiTree T)
{printf("树结点的值：%c\n", T->data);
}/*利用一个前序遍历的扩展二叉树的字符串序列*/
void CreateBiTree1(BiTree* T)
{Elemtype ch;scanf("%c", &ch); //获取前序遍历的扩展二叉树的字符串的一个字符if (ch == '#')*T = NULL; // 空树结点else{*T = (BiTree)malloc(sizeof(BiTNode));if (!*T)  // 未分配到空间exit(false);(*T)->data = ch;	// 生成根结点(*T)->lchild = (*T)->rchild = NULL;CreateBiTree1(&(*T)->lchild); // 构造左子树CreateBiTree1(&(*T)->rchild); // 构造右子树}
}

六、程序输出

前序遍历：

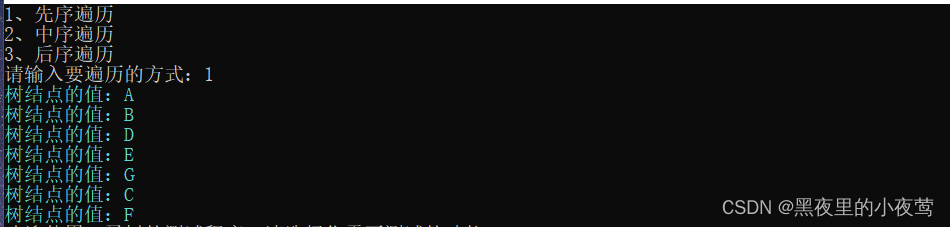
中序遍历：

后序遍历：

 

 

 


http://chatgpt.dhexx.cn/article/NPR4y5gx.shtml

相关文章

详细图解二叉树四种遍历(前序中序后序层次遍历)

详细图解二叉树四种遍历(前序中序后序层次遍历)

文章目录 一.前序遍历常规操作简单方法 二.中序遍历常规操作简单方法 三.后序遍历常规操作 四.层次遍历常规操作 本文中以此二叉树为例 一.前序遍历 常规操作 先根&#xff0c;再左&#xff0c;再右 确定了遍历整体结构&#xff1a; 确定了左子树中的整体结构 继续操作&…
阅读更多...
FPN细节剖析以及pytorch代码实现

FPN细节剖析以及pytorch代码实现

目录 FPN&#xff08;feature pyramid network&#xff09; 网络结构 bottleneck pytorch代码实现 公式&#xff1a;卷积层输入输出大小的计算公式 细节一&#xff1a;代码中blocks参数的含义 细节二&#xff1a;c1 c2 c3 c4 c5层尺寸分别为原图的1/2 1/4 1/8 1/16 1/32…
阅读更多...
目标检测之FPN、AugFPN、NAS-FPN

目标检测之FPN、AugFPN、NAS-FPN

针对小目标的检测有提升的文章。 未完待续~ Feature Pyramid Networks for Object Detection FPN是一种多尺度的目标检测算法。大多数目标检测算法都是采用顶层特征来做预测的&#xff0c;但是我们知道&#xff1a;低层的特征语义信息较少&#xff0c;但是位置信息丰富&#x…
阅读更多...
FPN网络和RPN网络介绍

FPN网络和RPN网络介绍

原文链接 神经网络特征提取过程中&#xff0c;一般底层特征具有良好的空间信息&#xff0c;高层的具有良好的语义信息。原来多数的object detection算法都是只采用顶层特征做预测&#xff0c;但我们知道低层的特征语义信息比较少&#xff0c;但是目标位置准确&#xff1b;高层…
阅读更多...
Neck网络 FPN + PAN 改进解读

Neck网络 FPN + PAN 改进解读

呃 这篇文章的目的在于补充一些知识以便于理解Neck部分的网络 特征提取网络 与 目标检测之间的关系 一个特征提取网络&#xff0c;假设有1000层&#xff0c;开始的特征图包含的细节信息就很多&#xff0c;而随着网络的加深&#xff0c;特征提取网络经过多次被卷积和池化操作&…
阅读更多...
FPN论文笔记

FPN论文笔记

FPN论文笔记 现在看FPN和Inception并行结构融合有点像&#xff0c;FPN上采样同时横向连接相加&#xff0c;Inception是堆叠几个感受野不同的feature&#xff0c;融合的思想有点相似。 FPN是什么&#xff1f; Feature Pyramid Networks,用于特征抽取&#xff08;feature extr…
阅读更多...
FPN算法一览

FPN算法一览

FPN应该是2017年CV顶会的优秀论文&#xff0c;基于目标检测做的研究&#xff0c;在小物体检测方面较为具有吸引力。 1.FPN 源论文&#xff1a;feature pyramid networks for object detection 参考代码&#xff1a;FPN 同时利用低层特征高分辨率和高层特征的高语义信息&…
阅读更多...
目标检测中的各种FPN

目标检测中的各种FPN

早期的目标检测算法&#xff0c;无论是一步式的&#xff0c;还是两步式的&#xff0c;通常都是在Backbone的最后一个stage&#xff08;特征图分辨率相同的所有卷积层归类为一个stage&#xff09;最后一层的特征图&#xff0c;直接外接检测头做目标检测。此种目标检测算法&#…
阅读更多...
FPN（在FasterRCNN里面是如何运用的）

FPN（在FasterRCNN里面是如何运用的）

FPN(Feature Pyramid Networks) FPN解决了什么问题&#xff1f; 答&#xff1a;FPN的提出是为了实现更好的feature maps融合&#xff0c;一般的网络都是直接使用最后一层的feature maps&#xff0c;虽然最后一层的feature maps 语义强&#xff0c;但是位置和分辨率都比较低&…
阅读更多...
深度学习之FPN+PAN

深度学习之FPN+PAN

一、FPN 检测不同尺度的物体具有挑战性&#xff0c;尤其是对于小物体&#xff0c;我们可以使用不同尺度的同一图像的金字塔来检测物体&#xff08;下左图&#xff09;但是&#xff0c;处理多尺度图像非常耗时并且内存需求太高而无法同时进行端到端训练&#xff0c;因此创建了一…
阅读更多...
FPN全解-最全最详细

FPN全解-最全最详细

这篇论文是CVPR2017年的文章&#xff0c;采用特征金字塔做目标检测&#xff0c;有许多亮点&#xff0c;特来分享。 论文&#xff1a;feature pyramid networks for object detection 论文链接&#xff1a;https://arxiv.org/abs/1612.03144 论文概述&#xff1a; 作者提出的…
阅读更多...
FPN和PAN的内容及区别

FPN和PAN的内容及区别

FPN和PAN都是用于解决在目标检测中特征金字塔网络(FPN)在多尺度检测任务上的不足的方法。下面分别详细介绍一下它们的原理和区别。 FPN FPN全称Feature Pyramid Network&#xff0c;是由FAIR在2017年提出的一种处理多尺度问题的方法。FPN的主要思路是通过构建金字塔式的特征图…
阅读更多...
深度学习之FPN和PAN

深度学习之FPN和PAN

注&#xff1a;借鉴整理&#xff0c;仅供自学&#xff0c;侵删 FPN是自顶向下&#xff0c;将高层的强语义特征传递下来&#xff0c;对整个金字塔进行增强&#xff0c;不过只增强了语义信息&#xff0c;对定位信息没有传递。PAN就是针对这一点&#xff0c;在FPN的后面添加一个自…
阅读更多...
FPN网络介绍

FPN网络介绍

目录 前言一.FPN网络二.网络创新点 前言 上一篇博文我们介绍了FCN结构&#xff0c;这篇博文我们来简答的介绍下FPN网络&#xff0c;FPN (Feature Pyramid Network) 是一种用于图像语义分割、物体检测等任务的神经网络结构。是针对目标检测提出的结构。 一.FPN网络 先来看下FP…
阅读更多...
FPN+PAN结构,SPP结构

FPN+PAN结构,SPP结构

一、FPNPAN FPN 高维度向低维度传递语义信息&#xff08;大目标更明确&#xff09; PAN 低维度向高维度再传递一次语义信息&#xff08;小目标也更明确&#xff09; 二、SPP 深层的feature map携带有更强的语义特征&#xff0c;较弱的定位信息。而浅层的feature map携带有…
阅读更多...
FPN+PAN结构学习

FPN+PAN结构学习

yolo4的neck结构采用该模式&#xff0c;我们将Neck部分用立体图画出来&#xff0c;更直观的看下两部分之间是如何通过FPN结构融合的。 如图所示&#xff0c;FPN是自顶向下的&#xff0c;将高层特征通过上采样和低层特征做融合得到进行预测的特征图。Neck部分的立体图像&#xf…
阅读更多...
FPN网络理解

FPN网络理解

1.什么是FPN fpn设计动机&#xff1a;1.高层特征向低层特征融合&#xff0c;增加低层特征表达能力&#xff0c;提升性能 2.不同尺度的目标可以分配到不同层预测&#xff0c;达到分而治之。 fpn设计细节&#xff1a;1*1的卷积是让最左侧的三个特征图的通道保持一致&#xff0c;从…
阅读更多...
FPN详述

FPN详述

简介 为了使用更多的语义信息&#xff0c;目标检测模型一般在卷积神经网络最后一层的特征图上进行后续操作&#xff08;随着不断地下采样&#xff0c;语义信息更丰富&#xff0c;空间信息更稀少&#xff09;&#xff0c;而这一层对应的下采样率一般是比较大的&#xff0c;如16…
阅读更多...
FPN与Unet的异同

FPN与Unet的异同

来源&#xff1a;目标检测的FPN和Unet有差别吗? - 知乎 (zhihu.com) 作者&#xff1a;CW不要無聊的風格 链接&#xff1a;https://www.zhihu.com/question/351279839/answer/1598104355 来源&#xff1a;知乎 著作权归作者所有。商业转载请联系作者获得授权&#xff0c;非商业…
阅读更多...
FPN以及其他结构FPN——Bi-FPN重点（仅供自己学习使用）

FPN以及其他结构FPN——Bi-FPN重点（仅供自己学习使用）

FPN FPN特征金字塔结构。 由于目标检测中对小物体检测很困难&#xff0c;因为卷积过程中&#xff0c;大物体的像素点多&#xff0c;小物体的像素点少&#xff0c;随着卷积的深入&#xff0c;大物体的特征容易被保留&#xff0c;小物体的特征越往后越容易被忽略。所以产生了FPN结…
阅读更多...
推荐文章

Copyright @ 2022~2023