王道谊
2020年3月
1. 传播动力学
“道生一,一生二,二生三,三生万物。” ---《道德经》
所谓“不积跬步无以至千里”,任何变化都是由点滴变化决定并发展起来的。知道所有的微观点滴变化,就能够掌握宏观变化。点滴变化决定并发展成宏观变化这一过程可以用动力学模型描述。点滴变化有时会被忽略,当充分显现时经常会势不可挡。有“风光人不觉,已著后园梅”,更有“山青花欲燃”。今天楼下迎春花开数朵儿,很快就多得数不过来了。
对点滴变化的研究,有两个方面。一个是研究引起变化的原因,这属于特定专业范畴,如研究新冠病毒的S蛋白和ACE2之间的亲和力;另一个方面是研究变化发展规律,从而预判宏观变化态势,这属于传播动力学范畴,如预测传播期、感染人数规模,评估防疫效果等。
传播动力学可见于小道消息传播,和传播者、接收者数量,以及传播者与接收者之间的互动频次有关。
类似的传播动力学还常用于网络信息传播、计算机病毒传播、商品/服务推荐、大型网络故障继发效应等。这里关注传染病。
2. 人群SIR划分
"The beginning of wisdom is the definition of terms." --- Socrates
在平静的日子里,大家自由地生活。有个调皮的小伙伴躁动不安,不幸中招,之后是他的亲戚朋友同事,再后来累及整个人群,如下图:
注:橙色表示刚中招,蓝色中招超一天。
考虑一种最简单的情况,新病毒和所有人都有亲和力,即所有人都是易感者,这样可以进行如下分类:
-
设总人数为N ,维持不变,不考虑自然生死和迁入迁出。
-
染病者治愈后有抗体不会再被感染,称为移出者(百毒不侵者),用集合R 表示(Removeds)。得此病不幸远去者,也归于此类。有些传染病,患者治愈后还可以被传染,那么移出者只包含这些最终不幸的患者。
-
中招的且没有治愈的人称为感染者(播散病毒者),用集合I(Infectives)表示。
-
还没有中过招的人称为易感者(小心提防者),用集合S(Susceptibles)表示。愈后无抗体的会重新回到S 。
-
某时刻t ,感染者占比为i(t),则感染人数为N·i(t) ; 移出者占比r(t) ,则移出者人数为N·r(t) ;易感者占比为s(t) ,则易感者人数为 N·s(t) 。显然,r(t)+i(t)+s(t)=1。
3. 自由传播传染
新病毒在作孽初期,还没有入医生的法眼,医疗机构和防疫部门还没有采取措施,病毒在逍遥地自由传播。不考虑治愈和死亡。
既然是研究点滴变化,我们就取一足够小时间段Δt 。最够小的时间段内感染人数增加可看作线性变化,和病毒散播者(感染者)数量成正比,和单位时间内每人平均有效接触数次数λ 成正比。因为感染者单位时间平均有效接触的λ 次中,接触易感者比例为s(t),所以引起传染的人数为λs(t)。这样可以得到以t 时刻为起点的Δt 内,感染者增加为:
对应的微分方程及其解为:
自由传播,没有考虑治愈情况下,人群分为S 和 I,且最终所有的人都会被感染。上述传播模型称为SI模型。SI模型只是在传染病发生初期有效,可以用来预测病例增加速度的峰值到来时间。λ 值越大,传染性越强,称为日接触率,此时t的单位为天。我们以1000万人口的城市为例,假设第1天,不知什么原因产生了一个突发病人。感染者比例和时间的关系如下图所示,λ 值为0.9时,感染人数超过99%需要24天;λ 值为1.3时,只需要16天。当然,本次新冠的λ 值要小得多。
挖掘λ 值的影响因素对于防疫工作非常重要。总的来讲,可以归结为如下几个方面:
-
传播途径。古登堡当年铸造的镜子,反射圣物上的反射光的反射光来救赎拿镜子人的罪孽,λ 值会大得惊人。“红眼病”,一见就妒,也不好控制。本次新冠主要是飞沫传染,有效接触距离为几米,“拱手不握手”就差不多避免了。值得注意的是,飞沫传染比体液传播的λ 值大的多,不可小觑。
-
人们的生活习惯。少聚会、勤洗手,显然可以有效降低λ 值,拥抱和贴面之类的问候,肯定会乐坏了新冠病毒。
-
隔离强度。要想减少甚至切断感染者和易感人群之间接触,最有效的办法是隔离。正如我们现在享受的居家时光,远程工作、网上学习。对于可敬的医生和各类保障支撑人员,不能居家,只能加强自我防护。
有效接触率λ 能够反映传染病之传染性的强弱,但总让人觉得不够直接。Anderson 等1992年提出了一个定义R0(基本再生数)用来反映传染性的强弱。R0定义如下:“the average number of secondary infections produced when one infected individual is introduced into a host population where everyone is susceptible”。在一个全部都是易感者人群中,引入一个感染者引发传染病,R0相当于一段时间内(可以是全部中招后)平均每个患者感染的人数。
套用一句俗话“一传十、十传百”。实际上传染过程是随机的,没这么简单,不过仍然可以部分说明问题。基于“一传十、十传百”,第一天引入一个患者;第二天新感染R0个;第三天新感染R02;...,第k天新感染R0(k-1),共有感染者:
由上式不难看出,R0<1时,传染病会逐渐消亡;R0>1时,传染病会爆发。R0越大,疫情发展会更快。如此看来,用R0值来衡量传染性的强弱更易懂一些。R0的计算可以采用两种方法,一个是根据流行病学调查,统计每个确诊者的密切接触者之中被感染的人数,计算均值得R0;另一种是通过建模计算R0。计算R0是要注意患者人群的差异,患者隔离状态差异等因素。在发病初期,R0会高,后期随着人们认识程度提高,患者被收治隔离的比例提高,R0会显著下降,λ 值也是如此。打败疫情,在数学上就要把R0降到1以下。
还是用上面的例子,对于1000万人口的城市,如果R0=3,基于“一传十、十传百”的方式,16天会使全部感染。如下图,大致相当于SI模型中λ 值为1.218对应的情况。
4. 治愈
"Cure Sometimes, Treat Often, Comfort Always." --- Hippocrates
在上述SI模型的基础上,我们再考虑救治因素。救治可以有效降低日接触率,同时减少感染者的数量,最终使每天出院的人数大于入院的人数,曙光就不远了。
假设每天治愈患者的比例为μ ,我们先考虑新增病例为0或很少时,现有确诊病例的变化情况。此时每天减少的病人为μ·N·i(t)。进一步简化,假设全部感染后再救治,治愈后不复发。即初始i(t)为1,于是:
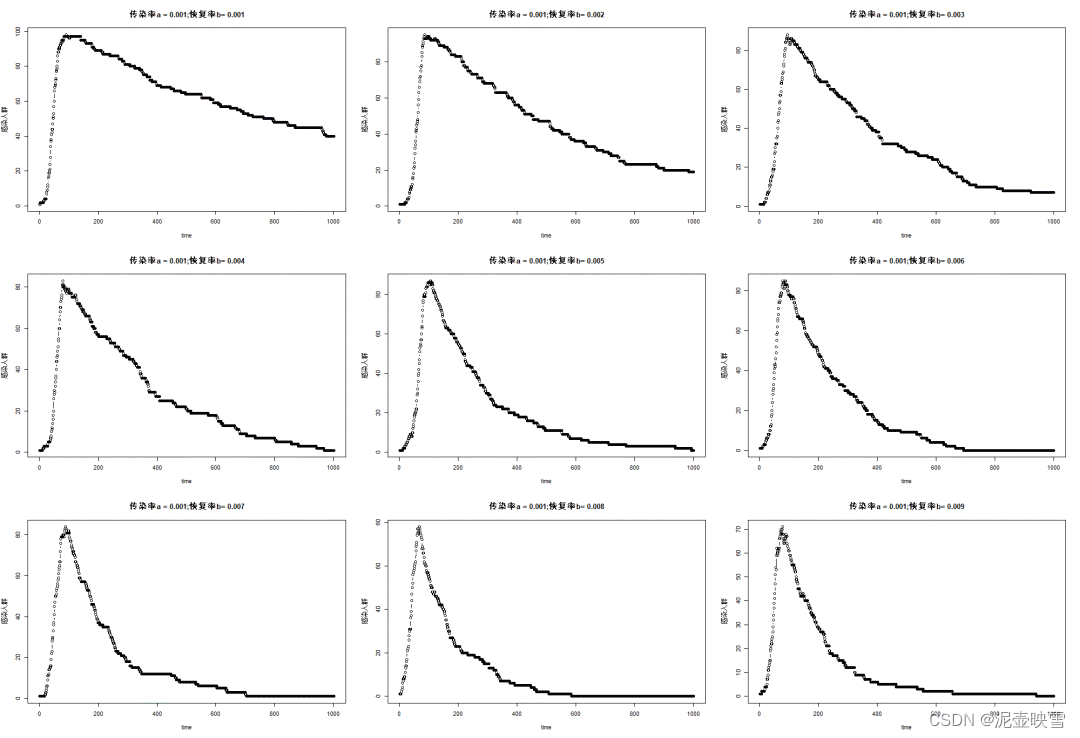
不同μ 值对应的i(t)~t 曲线如下图所示,救治水平提高的作用显而易见。
5. SIR模型
目前在国内基本控制住了,愈后有抗体,专家说会不会复发还有待研究。往好处想,有抗体就不复发了吧,所以治愈人群可以归类到移出者。另外专家说潜伏期也能传染,所以更省事了,不考虑incubation。于是一小时间段内的变化可表示如下:
对应的微分方程为:
上述方程没有解析解,但可以用数值方法计算,简单一点儿可以使用显示欧拉算法,花哨点儿可以使用二阶龙格-库塔法。更多的时候找个工具,直接求。其中λ 值反映传染性强弱,同时也反映该地区对此种传染病卫生防疫能力(卫生水平);μ 值反映该传染病对应的医疗救治水平,包括治疗效果和医疗资源(医疗水平)。
我用Excel表模拟了一个显示欧拉格式的微分方程数值解法,考虑如下因素:
-
1月20日,全国报告确诊病例近300例。这之前,其传染性还不广为人知(1月20日,钟院士答记者问公布“人传人”)。显然这时,λ 值大些,μ 值小些。
-
1月23日,武汉封城,全国的λ 值明显下降,μ 值略有提升(外省医疗资源相对充足)。
-
2月初,火神山和雷神山医院交付,方舱医院陆续落成,各地驰援湖北的最美逆行者相继抵鄂,λ 值明显下降,μ 值明显提升。
-
2月10日左右,武汉全城排查,之后全国新冠肺炎在压制状态下传播,λ 值再次下降,μ 值再度提升。
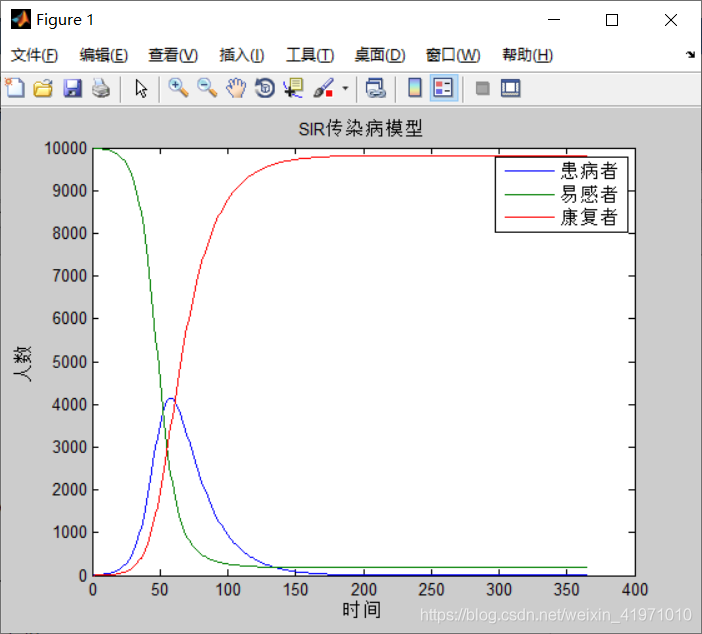
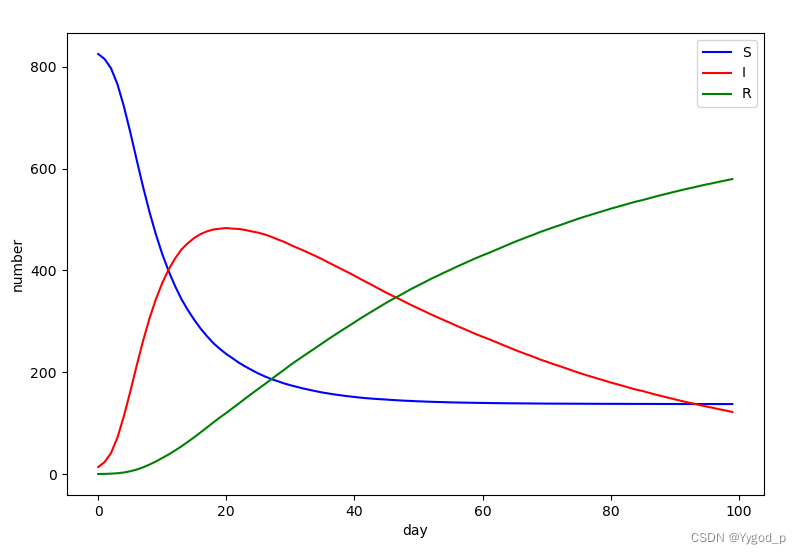
综合上述因素,利用数值计算解SIR模型对应的微分方程组得”现有确诊病例数随时间“变化曲线,如下图所示(示范一下,别太当真,真正能用的模型需要再认真点儿😀)。起点对应1月16日,高峰值出现在第36天后,对应2月21日。
把上图和下面来自今日头条网站的现有确诊疫情趋势图相比,是不是有几分神似^_^?

注:本图来自今日头条网站
从SIR模型的微分方程组中的第二个方程可以看出,当感染人数占比较小时(本次武汉最高千分之5左右),s(t) 约等于1, i(t) 的增加速度取决于(λ-μ)·i(t)。只有λ>μ,病例才会增加。因此,发现、认知、防控到解决,就是不断降低λ,提高μ。