算法能力是一个门槛，也是个有基础的门槛

无论你是iOS工程师，android工程师，java工程师，前端，后端还是全栈等等…

算法能力的强弱一方面在于思想，你是否有计算机思维抽象具体问题的能力

更重要的还在与基础了，如果你没有基础转化的能力，空有思想，在其他领域可能有助于你的工作效率问题，但在互联网尤其计算机从业方面无济于事

我是一名iOS工程师，但我不喜欢这样的定位，虽然现在公司的要求都会明确工种划分，但我自认为是个小强，我始终把自己定位称为一名计算机从业者，继续打怪升级

算法，是一个很好的试炼石

尤其是客户端程序员由于工作划分的原因，有很多人算法能力慢慢被弱化，工作上可能用不上，但我们客户端程序员不能找借口，市场是不会跟你商量的，尤其是年龄渐长之后，你pk的砝码又是什么呢

现在的客户端计算能力越来越强，手机上能处理的问题越来越多，手机的处理能力不弱于单台服务器，我们手机跟手机之间本身就是一个网络，是很重要的结点，那我们客户端的程序员们还有什么理由需要麻痹自己呢

快快行动起来吧，从算法基础开始，切不可被行业贴上了撕不掉的标签，总有一天，这个便签会完全限制掉你

本篇文章我想分享一个最小生成树，它并不是树，只是一种说辞

最小生成树是什么

首先了解图的概念

这是一个无向连通图，点之间的连线上的数字代表权重

最小生成树就是这个连通图子图并满足条件

• n个顶点，只会有n-1条边
• 最小生成树中 所有边 权重之和是最小的

最小生成树能做什么

我主要针对客户端程序员分享一些用途

可以考虑这样一个场景

• 一个app中包含很多功能页面，很多个场景，很多个入口

• 用户对于一款app的的使用习惯是多种多样的，随着app功能的迭代复杂，app的内容访问并不是线性的，而是相互重叠的

• 比如淘宝app，可以从搜索进入商品页，也可以从活动 - 产品直播 - 商品，还可以从商品 - 订单 - 详情 - 商品链接 - 直播间 - 商品

• 相信你已经看出来了，类似于这样的场景会很多，这是app产品复杂的结果

• 如果现在要对以往的功能进行用户数据统计，分析用户对于系列功能的黏度，功能使用的覆盖程度，使用频率分析，并根据分析结果进行调整

• 一般常规的做法是设计一套埋点框架，数据交给服务器，服务器来分析这些统计的数据

• 难道客户端就绑手绑脚了，只能做到这个程度

• 我觉得不然，从抽象角度看，app中的功能页面也好，功能点也好，用户对于app中各种功能的访问其实就是复杂的图结构而已

• 不同的用户沿着不同的路径进行探究，在图的路径上会延伸到各种功能结点，单个用户并不按照一定的规律访问

作为客户端程序员，你会怎么做

抛开所有的业务，这不就是一个求图的最小生成树问题么

• 客户端把用户的访问结点按照几天或者一周的时间维度抽象出来
• 把用户的结点跳转进行图中的边构建
• 解出构建连通图的最小生成树权重值
• 如果构建出来的图不是连通图，说明功能设计上有些不够圆滑，用户在某些功能跟功能之间是没有路径的，这就导致抽象出来的图不是连通的
• 每个用户的数据构建出来的图多少会有差异，怎么区分用户与用户呢
• 如果用户的功能结点够多，最终权重值比别的用户低，说明这个用户是比较纯粹的，对于功能的使用是比较单一的，不会反复跳切，也就是说不会因为app的功能版本升级马上关注
• 如果用户的权重值很高，说明是重度用户，可以统计这部分用户的比重，单个用户的分析就可由手机端处理完成，就不需要再由服务器端薅头发了，对于单用户的统计分析，客户端是占有很大优势的，离用户够近
• 如果用户的结点不多，但是计算的权重值也不是很低，说明可能卡在了某些功能入口处，用户不知道使用一些有门槛的功能入口进入，根据用户比重，可以考虑适当调整功能页面的分配，做个简单的调整

像这种例子，客户端会存在很多场景

最小生成树算法实现

在考虑怎么实现之前，你需要了解图的结构怎么存储

• 邻接矩阵

  • 如果要存储 A - B，也就是两点一线
  • 一个一维数组，存储顶点
  • 一个二维数组，存储边，也就是连线
  • 比如 A是0号元素，B是1号元素，array[0][1] 就代表 A-B的连线的权重

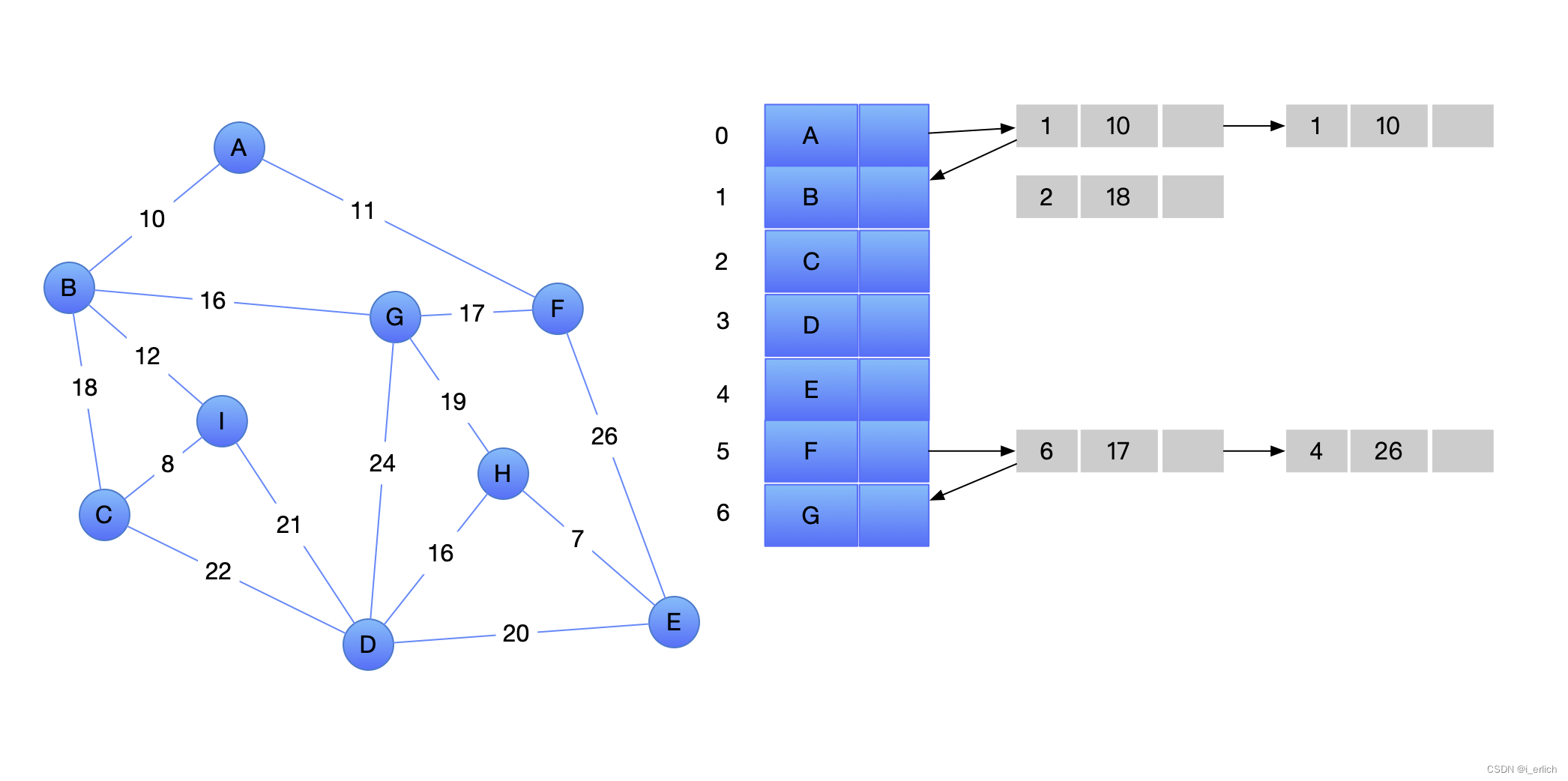
• 邻接表

  • 链接矩阵存储会存在空间的浪费，邻接表就出现了

  

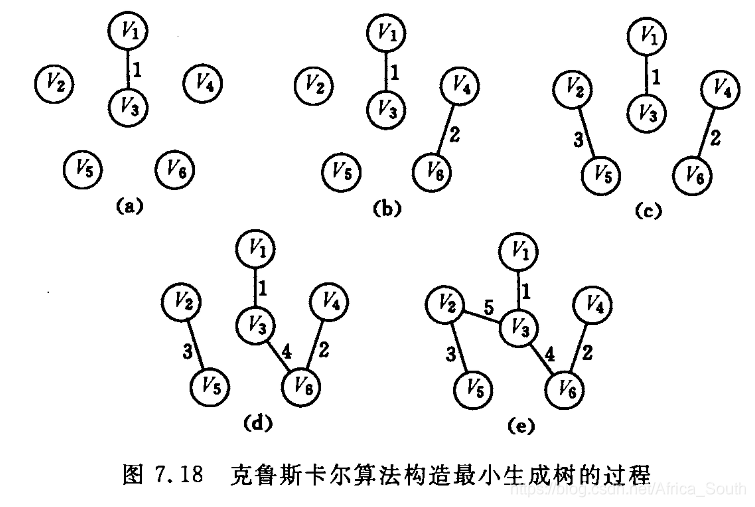
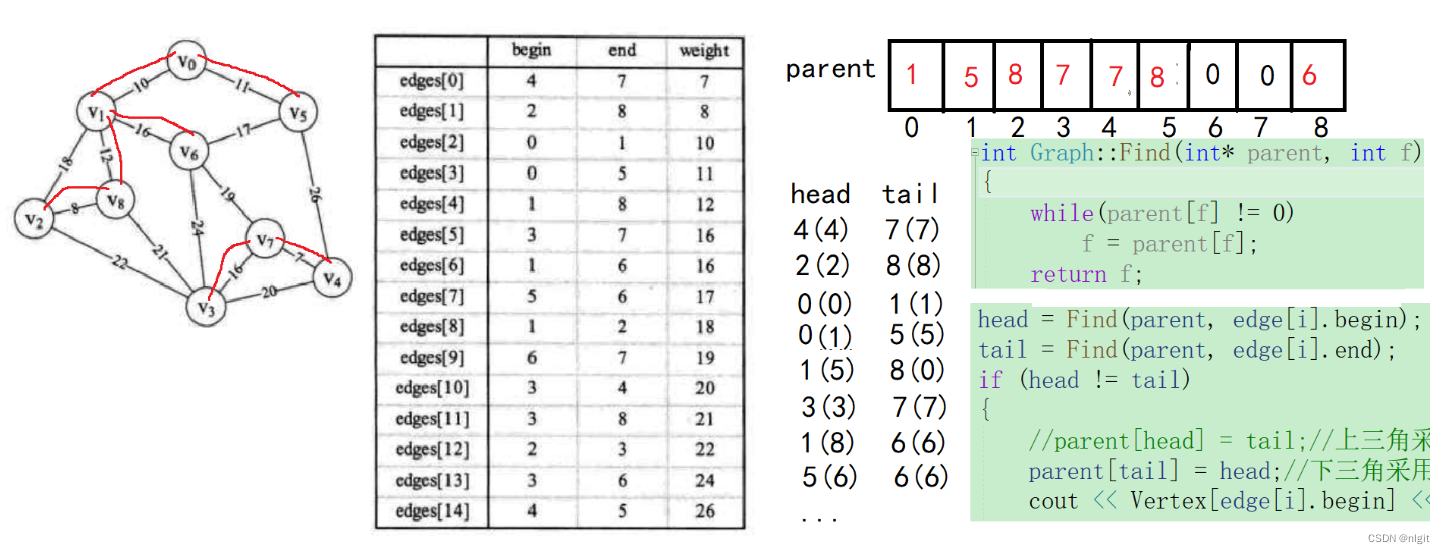
克鲁斯卡尔Kruskal算法

Kruskal是把邻接矩阵转换成 边表，也就是 15条边的数组，

每个元素包含结构 A - B(10) begin,end,weigh

数组按照权重大小排序

创建一维数组 parent，存储连通的下标

遍历边表数组，通过parent查找连通结点

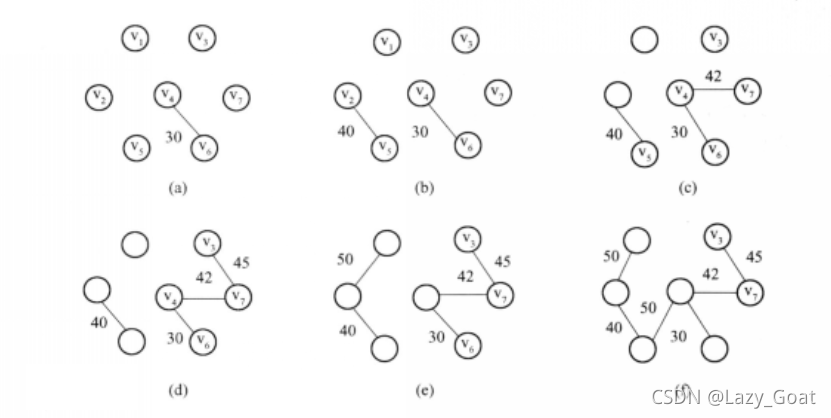
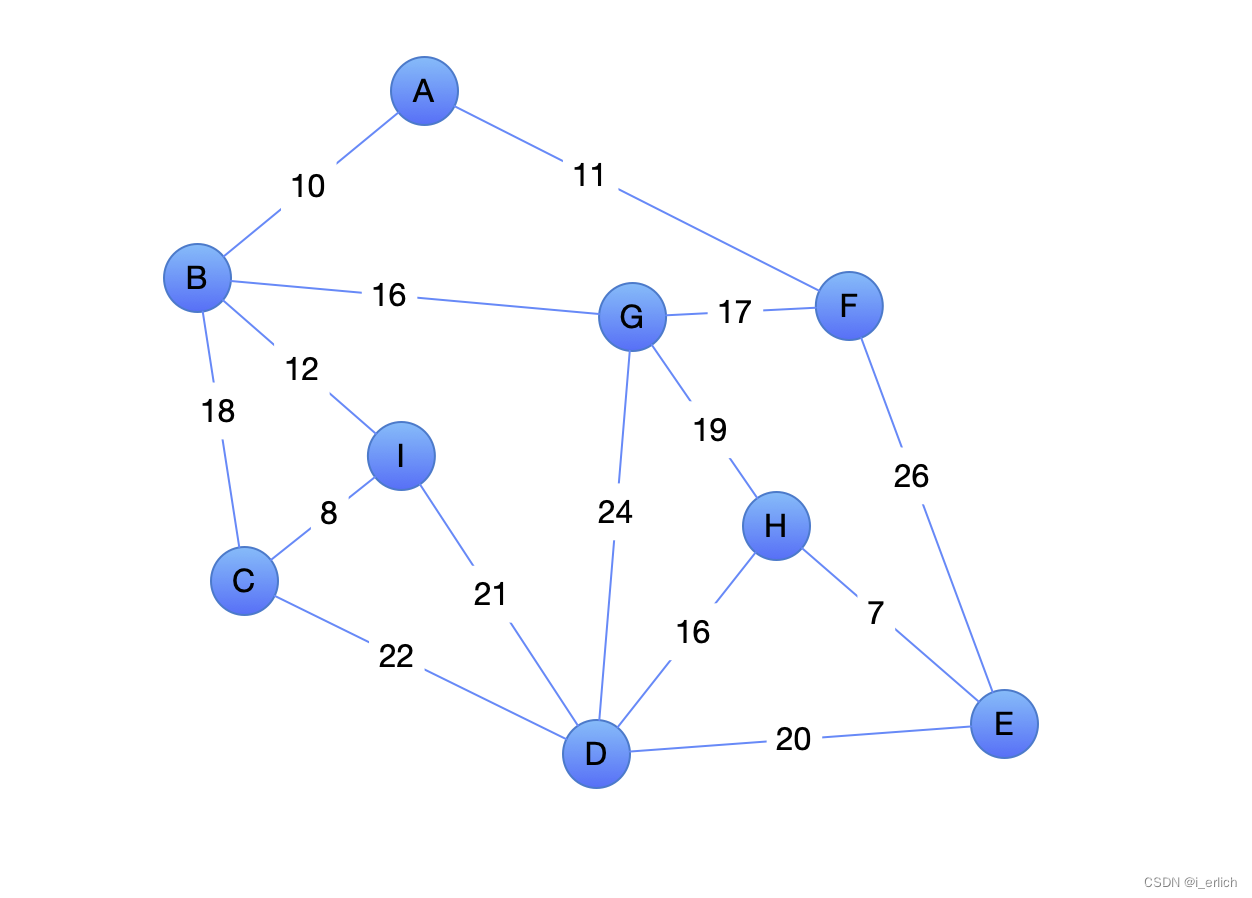
普里姆Prim算法

Prim是通过随意取一个开始顶点进行遍历

比如从A开始，有两条边，A-B(10), A-F(11)

选择权重小的 A-B(10)

B又有3个连接顶点 B-C B-I B-G

这个时候有4条边进行比较 B-C(18) B-I(12) B-G(16) A-F(11)

选择权重小的A-F(11)

F又有连接的结点 F-G(17) F-E(26)

有5条边进行比较 B-C(18) B-I(12) B-G(16) F-G(17) F-E(26)

依此规律进行

代码实现

以下代码部分囊括了

• 图的邻接矩阵实现方式
• 邻接表方式
• 图的遍历
  • 深度优先遍历
  • 广度优先遍历
• 最小生成树实现
  • 克鲁斯卡尔Kruskal算法
  • 普里姆Prim算法
• 还有具体构建实例图的输入数据，见代码后

// 深度优先遍历 - 邻接矩阵方式
#define VERTEXMAX       50  //最大顶点数
#define EDGEMAX         50  // 最大边数
#define GRAPH_INFINITY  65535 // 标识无穷#define TRUE 1
#define FALSE 0typedef char VertexType;
typedef int EdgeType;int verts_visit[VERTEXMAX];	 // 标识已遍历过的结点// 邻接矩阵存储结构
typedef struct MatrixGraph {VertexType verts[VERTEXMAX];                // 顶点EdgeType matrix[VERTEXMAX][VERTEXMAX];      // 邻接矩阵int num_vertex;     // 顶点数int num_edge;       // 边数int direct;         // true - 有向图   false - 无向图
} MatrixGraph;void CreateMatrixGraph(MatrixGraph *graph) {printf("输入顶点数:");scanf("%d", &graph->num_vertex);printf("输入边数:");scanf("%d", &graph->num_edge);printf("顶点数: %d, 边数: %d\n", graph->num_vertex, graph->num_edge);// 初始化，对角线 0， 其余 无穷for (int i = 0; i < graph->num_vertex; i++) {for (int j = 0; j < graph->num_vertex; j++) {if (i == j) {graph->matrix[i][j] = 0;} else {graph->matrix[i][j] = GRAPH_INFINITY;}}}for (int i = 0; i < graph->num_vertex; i++) {printf("输入第%d个顶点: ", i + 1);getchar();scanf("%c", &graph->verts[i]);}printf("顶点：");for (int i = 0; i < graph->num_vertex; i++) {printf("%c ", graph->verts[i]);}printf("\n");printf("有向图1 还是 无向图0: ");scanf("%d", &graph->direct);for (int k = 0; k < graph->num_edge; k++) {int i, j, w;printf("输入第%d条边(i, j, w): ", k + 1);   // w- 标识权重getchar();scanf("%d, %d, %d", &i, &j, &w);graph->matrix[i][j] = w;if (!graph->direct) {graph->matrix[j][i] = w;}}int edges = 0;for (int i = 0; i < graph->num_vertex; i++) {for (int j = i + 1; j < graph->num_vertex; j++) {if (graph->matrix[i][j] != 0 && graph->matrix[i][j] != GRAPH_INFINITY) {edges++;printf("<%c-%c>(%d) ", graph->verts[i], graph->verts[j], graph->matrix[i][j]);}}printf("\n");}printf("总共%d条边\n", edges);
}

// 邻接矩阵方式-深度优先遍历实现  第i个顶点
void MG_DFS(MatrixGraph *graph, int i) {verts_visit[i] = TRUE;printf("%c ", graph->verts[i]);for (int j = 0; j < graph->num_vertex; j++) {if (graph->matrix[i][j] != 0 && graph->matrix[i][j] != GRAPH_INFINITY && !verts_visit[j]) {MG_DFS(graph, j);}}
}// 可能包含非连通图
void MG_Traverse(MatrixGraph *graph) {printf("开始深度优先遍历\n");for (int i = 0; i < graph->num_vertex; i++) {verts_visit[i] = FALSE;}for (int i = 0; i < graph->num_vertex; i++) {if (!verts_visit[i]) {MG_DFS(graph, i);}}printf("\n");
}

// 邻接表存储结构
typedef struct EdgeNode {       // 表头指向的 结点， 标识边int table_index;            // 在table中的索引下标int weigh;                  // 权重struct EdgeNode *next;
} EdgeNode;typedef struct VertNode {VertexType ch;EdgeNode *firstEdgeNode;
} VertNode, AdjTable[100];typedef struct AdjGraph {AdjTable table;int arc_num;                // 边数int node_num;               // 结点数int direct;                 // 是否有向图
} AdjGraph, *AdjGraphLink;void CreteAdjTableGraph(MatrixGraph *graph, AdjGraphLink TG) {TG->direct = graph->direct;TG->node_num = graph->num_vertex;TG->arc_num = graph->num_edge;for (int i = 0; i < graph->num_vertex; i++) {TG->table[i].ch = graph->verts[i];TG->table[i].firstEdgeNode = NULL;}for (int i = 0; i < graph->num_vertex; i++) {for (int j = i + 1; j < graph->num_vertex; j++) {if (graph->matrix[i][j] != 0 && graph->matrix[i][j] != GRAPH_INFINITY) {EdgeNode *eNode = (EdgeNode *)malloc(sizeof(EdgeNode *));eNode->table_index = j;eNode->weigh = graph->matrix[i][j];eNode->next = NULL;if (TG->table[i].firstEdgeNode == NULL) {TG->table[i].firstEdgeNode = eNode;} else {eNode->next = TG->table[i].firstEdgeNode;TG->table[i].firstEdgeNode = eNode;}if (!TG->direct) {EdgeNode *eNode1 = (EdgeNode *)malloc(sizeof(EdgeNode *));eNode1->table_index = i;eNode->weigh = graph->matrix[j][i];eNode1->next = NULL;if (TG->table[j].firstEdgeNode == NULL) {TG->table[j].firstEdgeNode = eNode1;} else {eNode1->next = TG->table[j].firstEdgeNode;TG->table[j].firstEdgeNode = eNode1;}}}}}
}

// 深度优先遍历-邻接表方式实现 第i个顶点
void MG_DFS_adjtable(AdjGraphLink graph, int i) {verts_visit[i] = TRUE;printf("%c ", graph->table[i].ch);EdgeNode *p = graph->table[i].firstEdgeNode;while (p) {if (!verts_visit[p->table_index]) {MG_DFS_adjtable(graph, p->table_index);}p = p->next;}
}// 可能包含非连通图
void MG_Traverse_adjtable(AdjGraphLink graph) {printf("邻接表方式 - 开始深度优先遍历\n");for (int i = 0; i < graph->node_num; i++) {verts_visit[i] = FALSE;}for (int i = 0; i < graph->node_num; i++) {if (!verts_visit[i]) {MG_DFS_adjtable(graph, i);}}printf("\n");
}

// 邻接矩阵方式 - 判断是否完全连通图
bool MatrixGraph_Check_Completely_Connected(MatrixGraph *graph) {for (int i = 0; i < graph->num_vertex; i++) {verts_visit[i] = FALSE;}int loop_count = 0;for (int i = 0; i < graph->num_vertex; i++) {if (!verts_visit[i]) {loop_count++;MG_DFS(graph, i);}}if (loop_count > 1) {return false;}return true;
}
// 邻接表方式 - 判断是否完全连通图
bool AdjGraph_Check_Completely_Connected(AdjGraphLink graph) {for (int i = 0; i < graph->node_num; i++) {verts_visit[i] = FALSE;}int loop_count = 0;for (int i = 0; i < graph->node_num; i++) {if (!verts_visit[i]) {loop_count++;MG_DFS_adjtable(graph, i);}}if (loop_count > 1) {return false;}return true;
}

#define QUEUE_MAX  50
// 广度优先遍历 依赖 队列
typedef struct QueueNode {int data[QUEUE_MAX];int front;          // 队列的头int rear;           // 队列的尾
} QueueNode, *Queue;
void InitQueue(Queue queue) {queue->front = 0;queue->rear = 0;
}
bool QueueEmpty(Queue queue) {return queue->front == queue->rear;
}
bool QueueFull(Queue queue) {return (queue->rear + 1) % QUEUE_MAX == queue->front;
}
// 队首元素
int QueueHead(Queue queue) {return queue->front;
}
// 队尾元素
int QueueRear(Queue queue) {return queue->rear;
}
// 队列中元素长度
int QueueLen(Queue queue) {return (queue->rear - queue->front + QUEUE_MAX) % QUEUE_MAX;
}
// 入队
bool EnQueue(Queue queue, int data) {if (QueueFull(queue)) {return false;}queue->data[queue->rear] = data;queue->rear = (queue->rear + 1) % QUEUE_MAX;return true;
}
// 出队
bool DeQueue(Queue queue, int *data) {if (QueueEmpty(queue)) {return false;}*data = queue->data[queue->front];queue->front = (queue->front + 1) % QUEUE_MAX;return true;
}
// 遍历队列
void Queue_Traverse(Queue queue) {if (QueueEmpty(queue)) {return;}int i = queue->front;printf("队列中的元素:\n");while (queue->front != queue->rear) {printf("%d ", queue->data[i]);i = (i + 1) % QUEUE_MAX;}printf("\n");
}

// 邻接矩阵广度优先遍历
void BFS_MatrixTraverse(MatrixGraph *graph) {printf("邻接矩阵 广度优先遍历\n");// verts_visit 重置for (int i = 0; i < graph->num_vertex; i++) {verts_visit[i] = FALSE;}// 创建队列QueueNode qu;Queue queue = &qu;InitQueue(queue);// 防止出现 不连通图的情况for (int i = 0; i < graph->num_vertex; i++) {if (!verts_visit[i]) {verts_visit[i] = TRUE;printf("%c ", graph->verts[i]);// 入队if (!EnQueue(queue, i)) {printf("操作入队列出现异常....\n");return;}while (!QueueEmpty(queue)) {// 出队   i存储出队的元素if (!DeQueue(queue, &i)) {printf("操作出队列出现异常....\n");return;}// 遍历 出队的元素i 的结点 连通的其他结点for (int j = 0; j < graph->num_vertex; j++) {if (graph->matrix[i][j] != 0 && graph->matrix[i][j] != GRAPH_INFINITY && !verts_visit[j]) {verts_visit[j] = TRUE;printf("%c ", graph->verts[j]);if (!EnQueue(queue, j)) {printf("操作入队列出现异常....\n");return;}}}}}}printf("\n");
}

// 邻接表广度优先遍历
void BFS_AdjTraverse(AdjGraphLink graph) {printf("邻接表 广度优先遍历\n");// verts_visit 重置for (int i = 0; i < graph->node_num; i++) {verts_visit[i] = FALSE;}// 创建队列QueueNode qu;Queue queue = &qu;InitQueue(queue);// 防止出现 不连通图的情况for (int i = 0; i < graph->node_num; i++) {if (!verts_visit[i]) {verts_visit[i] = TRUE;printf("%c ", graph->table[i].ch);// 入队if (!EnQueue(queue, i)) {printf("操作入队列出现异常....\n");return;}while (!QueueEmpty(queue)) {// 出队   i存储出队的元素if (!DeQueue(queue, &i)) {printf("操作出队列出现异常....\n");return;}// 遍历 出队的元素i 的结点 连通的其他结点EdgeNode *enode = graph->table[i].firstEdgeNode;while (enode != NULL) {if (!verts_visit[enode->table_index]) {verts_visit[enode->table_index] = TRUE;printf("%c ", graph->table[enode->table_index].ch);if (!EnQueue(queue, enode->table_index)) {printf("操作入队列出现异常....\n");return;}}enode = enode->next;}}}}printf("\n");
}

//
void Prim_Mini_GenTree_MatrixGraph(MatrixGraph *graph) {// 1.确认是个连通图if (!MatrixGraph_Check_Completely_Connected(graph)) {printf("----oops, 当前图是个非连通图....\n");return;}int min;int sum = 0;        // 存储 最小生成树 各边的权重累加之和// 2.定义两个数组// curr_associated_vertindex - 关联的顶点 下标// curr_weigh_cost - 相关联的顶点之间的 权重weighsint curr_associated_vertindex[VERTEXMAX];int curr_weigh_cost[VERTEXMAX];// 第一个顶点 从 graph->verts[0]开始curr_associated_vertindex[0] = 0;       //curr_weigh_cost[0] = 0;                 // 表示 结点 已经加入到 最小生成树// 3.第一个结点已经加入到最小生成树， 对 以上两个数组进行初始化for (int i = 1; i < graph->num_vertex; i++) {curr_associated_vertindex[i] = 0;// 比如 第一个结点  已经找到了两条边， // 其余的边在矩阵里 都用 GRAPH_INFINITY标识，就表示不存在curr_weigh_cost[i] = graph->matrix[0][i];     }// 4.循环curr_weigh_cost数组，找到最小权值，并获取到 关键顶点  // (从1开始, 因为0已经加入最小生成树了)int keyvert, j;printf("\n");for (int i = 1; i < graph->num_vertex; i++) {min = GRAPH_INFINITY;j = 1;keyvert = 0;// 从1开始，找与 第一个结点有关的所有结点// 5.拿第一个结点举例//  5.1 - curr_associated_vertindex 中存储了 0结点 下标//  5.2 - 遍历 curr_weigh_cost 中所有 与 0结点 相连的 权值//  5.3 - 权值最小的，就把 相连结点 的下标 // 		存进 curr_associated_vertindex里while (j < graph->num_vertex) {// curr_weigh_cost里存放的是当前 相关的 结点// 比如刚开始 - 具体实现其实存了邻接矩阵 [0][j]  // 多个节点， 有些结点其实不存在，weight = 65535， // 只有一部分是正常的weigh 值if (curr_weigh_cost[j] != 0 && curr_weigh_cost[j] < min) {  // 如果 与结点 关联的结点 已经加入到了 最小生成树，// 会把 curr_weigh_cost中 相应位置的weigh 变为了0min = curr_weigh_cost[j];keyvert = j;}j++;}// curr_associated_vertindex[keyvert] 就存储了 上一次找到的结点printf("(V%d-V%d)(%c-%c)[%d]\n", curr_associated_vertindex[keyvert], keyvert,graph->verts[curr_associated_vertindex[keyvert]], graph->verts[keyvert],graph->matrix[curr_associated_vertindex[keyvert]][keyvert]);sum += graph->matrix[curr_associated_vertindex[keyvert]][keyvert];// keyvert加入最小生成树  为新增的结点 找到 与它有联系的 顶点curr_weigh_cost[keyvert] = 0;// 6. 然后把刚加入最小生成树的结点  相关的结点 找出来，// 		并找出当前节点 相连的结点//  6.1 - 权值最小的结点 下标 存进 curr_associated_vertindex里//  6.2 - 结点的最小权值 存进 curr_weigh_cost里//  6.3 - 这样 curr_associated_vertindex里包含了 // 			需要参与比较的结点 下标//          curr_weigh_cost里 包含了 以上结点 相关联 的边的 权重for (j = 1; j < graph->num_vertex; j++) {// curr_weigh_cost 很多位置 默认你会存储 无穷大// 还有一种情况， 如果别的结点 与 循环的当下结点  // 		都 与另外同一个节点关联，哪个小就留哪个if (curr_weigh_cost[j] != 0 && graph->matrix[keyvert][j] < curr_weigh_cost[j]) {curr_weigh_cost[j] = graph->matrix[keyvert][j];// 解释意思： 新加到生成树的结点， 找出与此结点相连的所有结点// 找到了，就把 相连的点index 加入到 //		curr_associated_vertindex中// 注意：此时加入到 curr_associated_vertindex //		中的是 curr_weigh_cost的 索引// 因为下次要比较  所有与 点相关的 权值最小的curr_associated_vertindex[j] = keyvert;// 比如   v1 结点 连接了 v8 v2 v6 三个顶点// 则  curr_associated_vertindex 中存储 // 			就是  0 0 1 0 0 0 1 0 1// 三个顶点都 存储了 1}}}printf("最小生成树 权重： %d\n", sum);}

typedef struct Kruskal_Edge {int begin;int end;int weigh;
} KEdge;void swap(KEdge array[], int i, int j) {KEdge temp = array[i];array[i] = array[j];array[j] = temp;
}void q_sort(KEdge array[], int left, int right) {if (right < left) {return;}int mid_i = left;int l = left;int r = right;while (l < r) {while (l < r && array[r].weigh >= array[mid_i].weigh) {r--;}while (l < r && array[l].weigh <= array[mid_i].weigh) {l++;}if (l < r) {swap(array, l, r);}}swap(array, left, l);q_sort(array, left, l - 1);q_sort(array, r + 1, right);
}void quicksort(KEdge array[], int n) {q_sort(array, 0, n - 1);
}int find(int *parent, int f) {while (parent[f] > 0) {f = parent[f];}return f;
}// Kruskal - 邻接矩阵 - 最小生成树
// 转化成边表数组
void Kruskal_Mini_GenTree_MatrixGraph(MatrixGraph *graph) {KEdge *edges = (KEdge *)malloc(sizeof(KEdge) * graph->num_edge);int index = 0;for (int i = 0; i < graph->num_vertex; i++) {for (int j = i + 1; j < graph->num_vertex; j++) {if (graph->matrix[i][j] != GRAPH_INFINITY) {KEdge edge;edge.begin = i;edge.end = j;edge.weigh = graph->matrix[i][j];edges[index] = edge;index++;}}}printf("邻接矩阵转换为边表:\n");for (int i = 0; i < graph->num_edge; i++) {printf("(%d, %d, %d)\n", edges[i].begin, edges[i].end, edges[i].weigh);}printf("\n");int *parent = (int *)malloc(sizeof(int) * graph->num_vertex);for (int i = 0; i < graph->num_vertex; i++) {parent[i] = 0;}// 边表数组 按照权值排序quicksort(edges, graph->num_edge);//int m = 0, n = 0;int sum = 0;for (int i = 0; i < graph->num_edge; i++) {n = find(parent, edges[i].begin);m = find(parent, edges[i].end);if (n != m) {parent[n] = m;printf("(V%d-V%d)(%c-%c)[%d]\n", edges[i].begin, edges[i].end,graph->verts[edges[i].begin],graph->verts[edges[i].end],edges[i].weigh);sum += edges[i].weigh;}}printf("Kruskal 最小生成树 总权重：%d\n", sum);
}

void test_graph_mini_gentree(void) {MatrixGraph graph;CreateMatrixGraph(&graph);MG_Traverse(&graph);// 用邻接矩阵的数据 初始化 邻接表AdjGraph adj_table_graph;CreteAdjTableGraph(&graph, &adj_table_graph);MG_Traverse_adjtable(&adj_table_graph);// 邻接矩阵广度优先遍历BFS_MatrixTraverse(&graph);// 邻接表广度优先遍历BFS_AdjTraverse(&adj_table_graph);// prim最小生成树 - 邻接矩阵printf("prim - 邻接矩阵方式 - 最小生成树: \n");Prim_Mini_GenTree_MatrixGraph(&graph);// kruskal 最小生成树 - 邻接矩阵printf("kruskal - 邻接矩阵方式 - 最小生成树: \n");Kruskal_Mini_GenTree_MatrixGraph(&graph);
}

构建数据

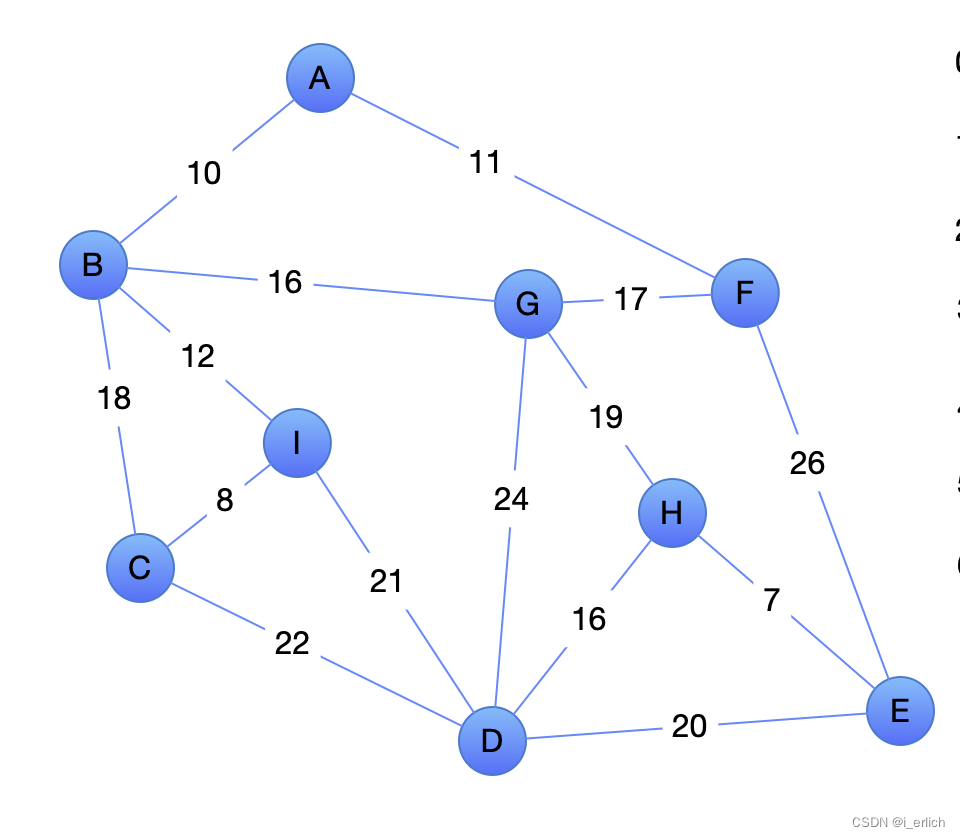
A B C D E F G H I
0 1 2 3 4 5 6 7 8
输入第1条边(i, j): 0,1 权重 10
输入第2条边(i, j): 0,5 11
输入第3条边(i, j): 1,6 16
输入第4条边(i, j): 5,6 17
输入第5条边(i, j): 1,8 12
输入第6条边(i, j): 6,7 19
输入第7条边(i, j): 1,2 18
输入第8条边(i, j): 8,2 8
输入第9条边(i, j): 2,3 22
输入第10条边(i, j): 8,3 21
输入第11条边(i, j): 6,3 24
输入第12条边(i, j): 7,3 16
输入第13条边(i, j): 7,4 7
输入第14条边(i, j): 3,4 20
输入第15条边(i, j): 5,4 26