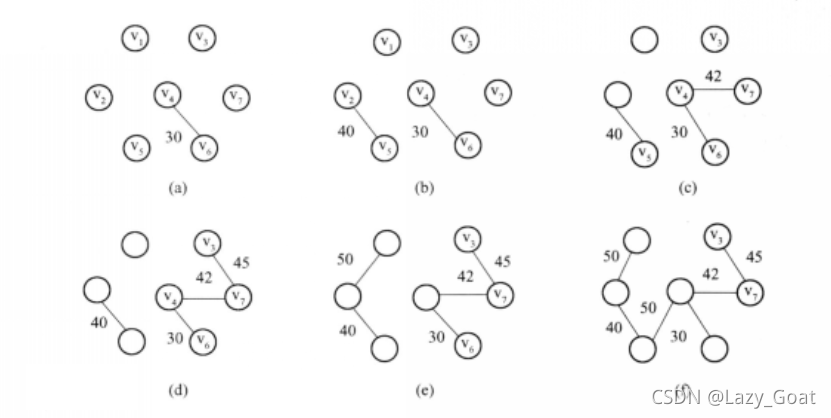
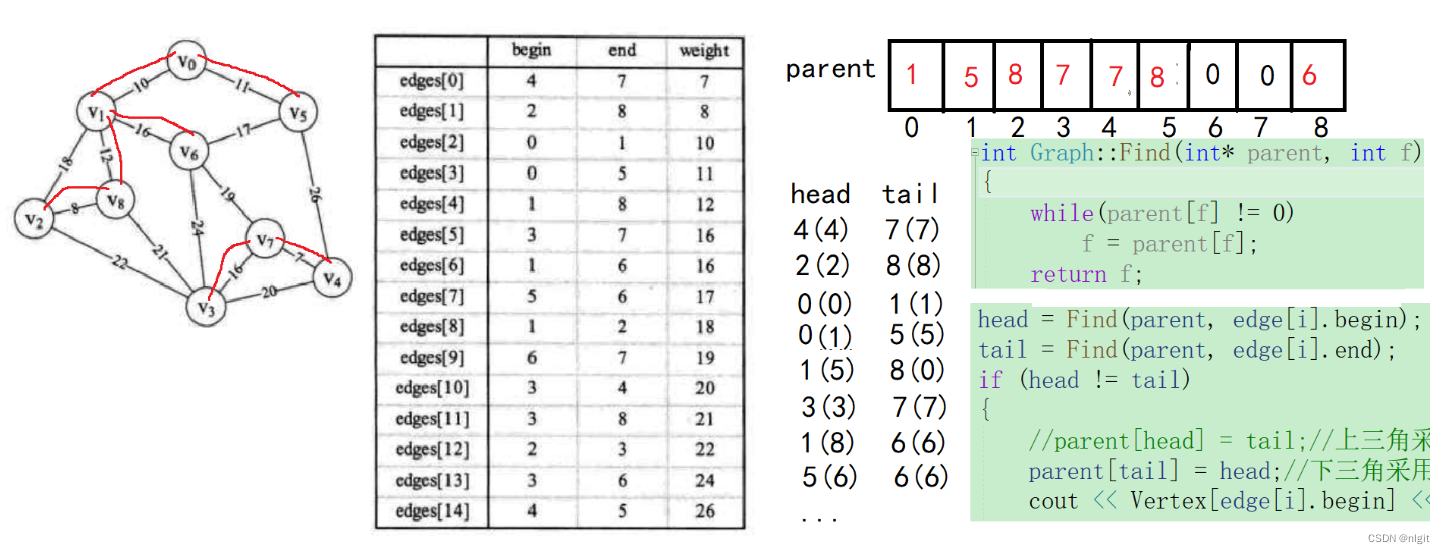
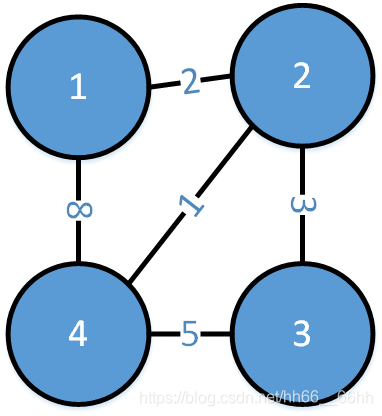
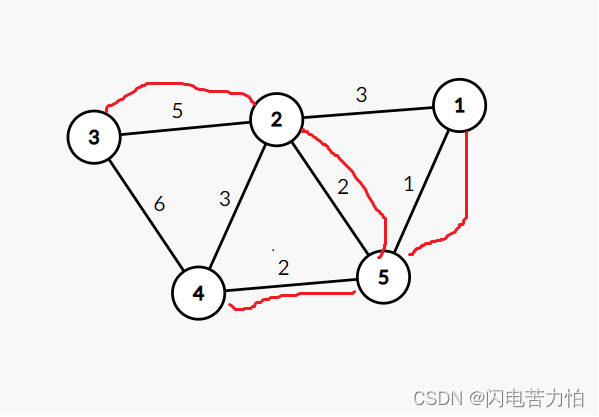
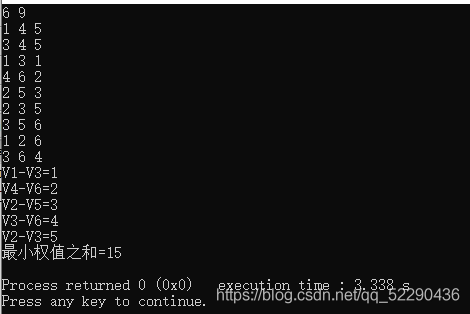
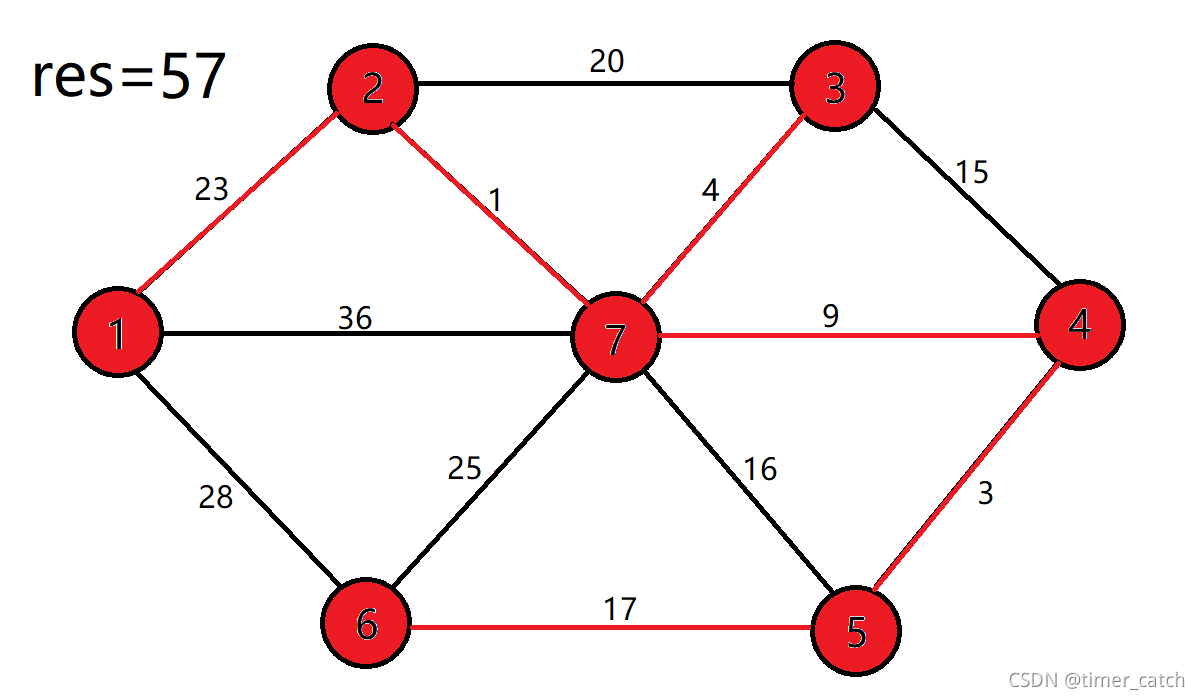
求这个网的最小生成树

/** 普里姆算法和克鲁斯卡尔算法求最小生成树* 采用邻接矩阵存储**/
#include<stdio.h>#define MAX_VERTEX_NUM 20
//图的定义
typedef struct 
{int vertexNum;int edgeNum;char vertex[MAX_VERTEX_NUM];int arc[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
}Graph,*PGraph;//辅助数组元素
typedef struct 
{int from;int to;int weight;int flag;
}ArrayNode; //构造无向网
void createdGraph(PGraph g)
{int i,j;g->vertexNum=6;g->edgeNum=10;for(i=0;i<g->vertexNum;i++)g->vertex[i]='A'+i;for(i=0;i<g->vertexNum;i++)for(j=0;j<g->vertexNum;j++)g->arc[i][j]=0;g->arc[0][1]=6;g->arc[0][2]=1;g->arc[0][3]=5;g->arc[1][0]=6;g->arc[1][2]=5;g->arc[1][4]=3;g->arc[2][0]=1;g->arc[2][1]=5;g->arc[2][3]=5;g->arc[2][4]=6;g->arc[2][5]=4;g->arc[3][0]=5;g->arc[3][2]=5;g->arc[3][5]=2;g->arc[4][1]=3;g->arc[4][2]=6;g->arc[4][5]=6;g->arc[5][2]=4;g->arc[5][3]=2;g->arc[5][4]=6;
}//初始化最小生成树
void initTree(PGraph tree)
{int i,j;tree->vertexNum=6;tree->edgeNum=5;for(i=0;i<tree->vertexNum;i++)tree->vertex[i]='0';for(i=0;i<tree->vertexNum;i++)for(j=0;j<tree->vertexNum;j++)tree->arc[i][j]=0;
}//普里姆算法求最小生成树
void prim(PGraph g,PGraph tree)
{int i,j,k;int index;  //指向权值最小的边ArrayNode  edgeArray[MAX_VERTEX_NUM*2]; //辅助数组 int length=0; //数组长度int n=1;  //统计数组已加入多少个顶点//初始状态把第一个顶点加入树中tree->vertex[0]='A';printf("%-3c",tree->vertex[0]);i=0;while(1){//寻找与顶点i相接且这条边的另一个顶点不在树中的边,存入edgeArray数组中for(j=0;j<g->vertexNum;j++){if(g->arc[i][j] > 0){//判断这条边的另一个顶点在不在树中for(k=0;k<tree->vertexNum;k++){if(tree->vertex[k] == g->vertex[j])break;}if(k == tree->vertexNum){edgeArray[length].from=i;edgeArray[length].to=j;edgeArray[length].weight=g->arc[i][j];edgeArray[length].flag=0;length++;}}}//从数组中选择权值最小的边index=-1;for(j=0;j<length;j++){if(index == -1 && edgeArray[j].flag == 0)index=j;if(edgeArray[j].flag==0 && edgeArray[j].weight < edgeArray[index].weight)index=j;}//在树中加入一个顶点，且把这条权值最小的边加入树中tree->vertex[edgeArray[index].to]='A'+edgeArray[index].to;edgeArray[index].flag=1;tree->arc[edgeArray[index].from][edgeArray[index].to]=edgeArray[index].weight;tree->arc[edgeArray[index].to][edgeArray[index].from]=edgeArray[index].weight;//当这个顶点加入树中时，与这个顶点相邻的边不可加入树中for(k=0;k<length;k++){if(edgeArray[k].to == edgeArray[index].to)edgeArray[k].flag=1;}i=edgeArray[index].to;printf("%-3c",tree->vertex[i]);n++;//当有g->vertexNum个顶点时，最小生成树构造完成if(n==g->vertexNum)break;}
}//判断两个顶点是否连通（广度优先搜索）
int connected(PGraph tree,int from,int to)
{int i,j,k;int vertex[MAX_VERTEX_NUM];//看成队列int front,rear;if(from==to)return 1;front=rear=0;//把第一个顶点存入数组vertex[rear++]=from;//遍历treewhile(front<=rear){i=vertex[front];for(j=0;j<tree->vertexNum;j++)if(tree->arc[i][j]>0){if(j==to)return 1;//判断此顶点是否在队列中for(k=0;k<rear;k++)if(vertex[k] == j)break;if(k==rear)vertex[rear++]=j;}front++;}return 0;
}//克鲁斯卡尔算法求最小生成树
void kruskal(PGraph g,PGraph tree)
{ArrayNode  edgeArray[MAX_VERTEX_NUM]; //辅助数组 int length=0;int i,j,k,index,n;//顶点先加入树中for(i=0;i<tree->vertexNum;i++)tree->vertex[i]=i+'A';//1.把所有的边有序(从小到大)的插入edgeArray数组中for(i=0;i<g->vertexNum;i++)for(j=0;j<g->vertexNum;j++){if(i<j && g->arc[i][j]>0){//寻找插入的位置indexfor(k=0;k<length;k++){if(edgeArray[k].weight > g->arc[i][j])break;}index=k;//移位for(k=length;k>index;k--)edgeArray[k]=edgeArray[k-1];//插入length++;edgeArray[index].flag=0;edgeArray[index].from=i;edgeArray[index].to=j;edgeArray[index].weight=g->arc[i][j];}}//2.从小到大取出n-1条边构造最小生成树n=0;while(n < g->vertexNum-1){//从小到大取一条符合要求的边for(k=0;k<length;k++)if(edgeArray[k].flag==0 && connected(tree,edgeArray[k].from,edgeArray[k].to)==0){break;}//把这条边加入树中tree->arc[edgeArray[k].from][edgeArray[k].to]=edgeArray[k].weight;tree->arc[edgeArray[k].to][edgeArray[k].from]=edgeArray[k].weight;edgeArray[k].flag=1;printf("%-3d",edgeArray[k].weight);n++;}
}void main()
{Graph graph;Graph tree;createdGraph(&graph);initTree(&tree);printf("普里姆算法树中顶点加入的顺序:\n");prim(&graph,&tree);printf("\n");initTree(&tree);printf("克鲁斯卡尔算法树中边加入的顺序:\n");kruskal(&graph,&tree);printf("\n");
}