图——最小生成树

1. 基本概念

在一个连通无向图G=(V, E)中，对于其中的每条边(u,v)∈E，赋予其权重w(u, v)，则最小生成树问题就是要在G中找到一个连通图G中所有顶点的无环子集T⊆E，使得这个子集中所有边的权重之和w(T) = $\displaystyle\sum_{(u,v)∈T} w(u, v)$ 最小。显然，T必然是一棵树，这样的树通常称为图G的生成树。

2. 最小生成树算法

通常来说，要解决最小生成树问题，通常采用两种算法：Prim算法和Kruskal算法。先假设要求一个连通无向图G=(V, E)的最小生成树T，且以其中的一个顶点V1为T的根结点。下面就分别对这两种算法进行介绍。

2.1 Prim算法

2.1.1 基本思想

Prim算法构建最小生成树的过程是：先构建一棵只包含根结点V1的树A，然后每次在连接树A结点和图G中树A以外的结点的所有边中，选取一条权重最小的边加入树A，直至树A覆盖图G中的所有结点。

注意：在这个算法中，关键点在于在连接树A结点和图G中树A以外的结点的所有边中选取权重最小的边。在算法实现过程中，要记录G中每个结点i到树A中结点的最小距离minidistance[i]，以及与之相连的树A中的那个结点miniadj[i]。minidistance[i]开始都初始化为无穷大，miniadj[i]都初始化为该顶点自己；每将一个结点j加入了树A，首先令minidistance[j]=0，然后遍历图G中所有不在树A中的结点，看看往树A中加入了结点j后，这些结点到树A中结点的最小距离会不会变小，如果变小则进行调整。例如，对于结点k，它在图G中，但不在树A中，且结点k与结点j相连，该边的权重为w(k, j)。在未将结点j加入树A前，结点k到树A中结点的最小距离为minidistance[k]；将结点j加入树A后，如果minidistance[k] > w(k, j)，那么结点k到树A中结点的最小距离就是结点k到结点j的最小距离，所以要将minidistance[k]调整为w(k, j)，且miniadj[k]为j。

例子
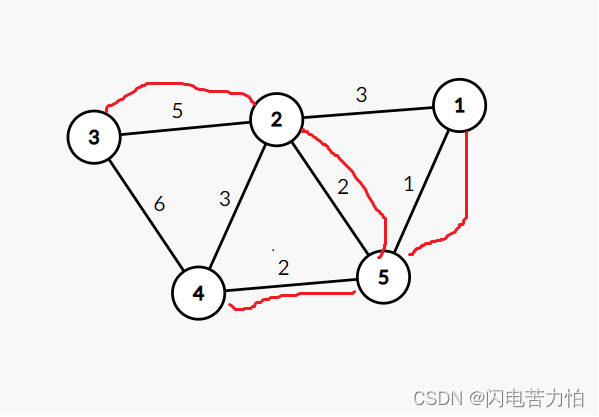
有一个无向连通图G，它有5个顶点，7条边，如下图所示。
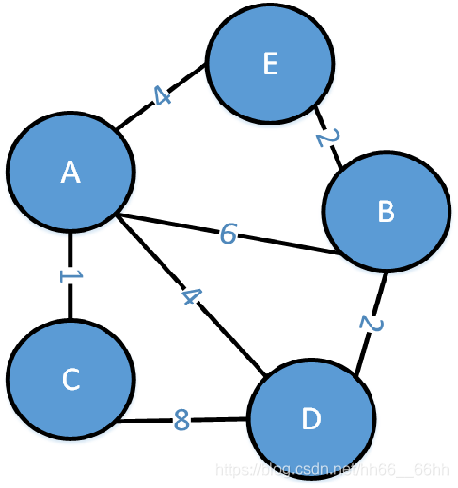
在这里插入图片描述
以结点A最为根结点，利用Prim算法来生成该图的最小生成树T的过程如下：
（1）开始T为空，初始化minidistance[A] = minidistance[B] = minidistance[C] = minidistance[D] = minidistance[E] = ${\infty}$ ，miniadj[A] = A，miniadj[B] = B, miniadj[C] = C，miniadj[D] = D，miniadj[E] = E；

（2）将结点A加入T，这时minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 6，miniadj[B] = A ，minidistance[C] = 1，miniadj[C] = A , minidistance[D] = 4，miniadj[D] = A , minidistance[E] = 4,miniadj[E] = A 。

（3）此时结点B,C,D,E都不在树T中，在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[C]，且miniadj[C]=A，所以将结点C和结点C与结点A连成的边加入树T。此时，minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 6，miniadj[B] = A ，minidistance[C] = 0，miniadj[C] = A , minidistance[D] = 4，miniadj[D] = A , minidistance[E] = 4,miniadj[E] = A 。

（4）此时结点B,D,E都不在树T中，在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[D]和minidistance[E]，从中随便选一个，此处选结点D，且miniadj[D]=A，所以将结点D和结点D与结点A连成的边加入树T。此时，minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 2，miniadj[B] = D ，minidistance[C] = 0，miniadj[C] = A , minidistance[D] = 0，miniadj[D] = A , minidistance[E] = 4,miniadj[E] = A 。

（5）此时结点B,E都不在树T中，在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[B]，且miniadj[B]=D，所以将结点B和结点B与结点D连成的边加入树T。此时，minidistance[A] = 0，miniadj[A] = A， minidistance[B] = 0，miniadj[B] = D ，minidistance[C] = 0，miniadj[C] = A , minidistance[D] = 0，miniadj[D] = A , minidistance[E] = 2,miniadj[E] = B。

（6）此时只有结点E都不在树T中，因此在连接树T结点和图G中树A以外的结点的所有边中，权重最小的边是minidistance[E]，且miniadj[E]=B，所以将结点E和结点E与结点B连成的边加入树T，此时最小生成树构成，如下图所示：
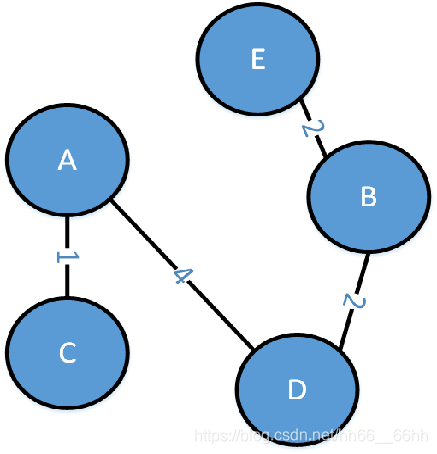
在这里插入图片描述

2.1.2 代码实现

#define Maximum 1000
#define Biggest 100000000typedef struct EdgeListNode{int adjId;int weight;EdgeListNode* next;
};typedef struct VertexListNode{int data;EdgeListNode* firstadj;
};typedef struct GraphAdjList{int vertexnumber;int edgenumber;VertexListNode vertextlist[Maximum];
};typedef struct MiniTreeEdge {int s;int e;int weight;MiniTreeEdge *next;
};typedef struct MiniTree {  //最小生成树MiniTreeEdge *head;  //指向最小生成树的根节点int vertextnumber;
};void MiniSpanTree_Prim(GraphAdjList g, MiniTree tree, int start_node) {tree.head = NULL;int *distance = (int*)malloc(sizeof(int) * g.vertexnumber + 2);int *miniadj = (int*)malloc(sizeof(int) * g.vertexnumber + 2);int i, j, k, lastnode, thisnode;lastnode = start_node;for(i=1; i<=g.vertexnumber; i++) {distance[i] = Biggest;miniadj[i] = i;}distance[start_node] = 0;tree.vertextnumber = 1;while(tree.vertextnumber < g.vertexnumber) {EdgeListNode *temp = g.vertextlist[lastnode].firstadj;while(temp != NULL) {j = temp->adjId;if(distance[j] && distance[j]>temp->weight) {distance[j] = temp->weight;miniadj[j] = lastnode;}temp = temp->next;}k = Biggest;for(i=1; i<=g.vertexnumber; i++) {if(distance[i] && k>distance[i]) {k = distance[i];thisnode = i;}}MiniTreeEdge *temp1 = (MiniTreeEdge*)malloc(sizeof(MiniTreeEdge));temp1->e = thisnode; //新加入的结点temp1->s = miniadj[thisnode]; //最小生成树中与新加入结点相连的结点temp1->weight = k; //新加入的边的权重temp1->next = NULL;temp1->next = tree.head;tree.head = temp1;distance[thisnode] = 0;lastnode = thisnode;tree.vertextnumber++;}//打印最小生成树MiniTreeEdge *e = tree.head;while(e != NULL) {cout<<e->s<<" -> "<<e->e<<"  :  "<<e->weight<<endl;e = e->next;}}

2.1.3 测试

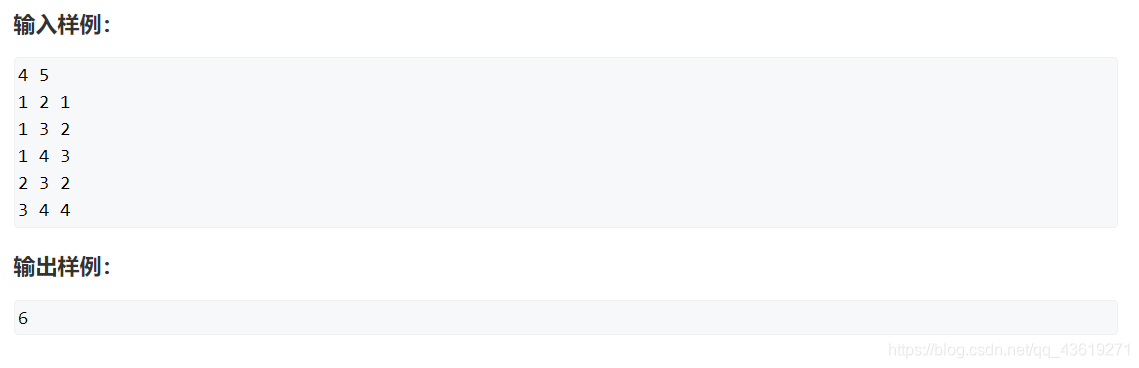
测试的图为：
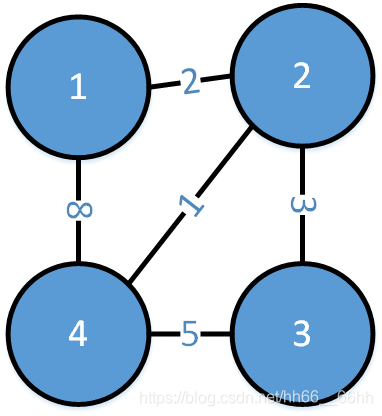
在这里插入图片描述

int main() {GraphAdjList g;g.edgenumber = 5;g.vertexnumber = 4;int i, j, k;EdgeListNode *temp;for(i=1; i<=4; i++) {g.vertextlist[i].data = i;g.vertextlist[i].firstadj = NULL;}temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 2; temp->weight = 2; temp->next = g.vertextlist[1].firstadj;g.vertextlist[1].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 4; temp->weight = 8; temp->next = g.vertextlist[1].firstadj;g.vertextlist[1].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 1; temp->weight = 2; temp->next = g.vertextlist[2].firstadj;g.vertextlist[2].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 3; temp->weight = 3; temp->next = g.vertextlist[2].firstadj;g.vertextlist[2].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 4; temp->weight = 1; temp->next = g.vertextlist[2].firstadj;g.vertextlist[2].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 2; temp->weight = 3; temp->next = g.vertextlist[3].firstadj;g.vertextlist[3].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 4; temp->weight = 5; temp->next = g.vertextlist[3].firstadj;g.vertextlist[3].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 1; temp->weight = 8; temp->next = g.vertextlist[4].firstadj;g.vertextlist[4].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 2; temp->weight = 1; temp->next = g.vertextlist[4].firstadj;g.vertextlist[4].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 3; temp->weight = 5; temp->next = g.vertextlist[4].firstadj;g.vertextlist[4].firstadj = temp;MiniTree tree;MiniSpanTree_Prim(g, tree, 1);MiniTreeEdge *e = tree.head;while(e != NULL) {cout<<e->s<<" -> "<<e->e<<"  :  "<<e->weight<<endl;e = e->next;}return 0;
}

2.2 Kruskal算法

2.2.1 基本思想

假设现在要求无向连通图G=(V, E)的最小生成树T，Kruskal算法的思想是令T的初始状态为|V|个结点而无边的非连通图，T中的每个顶点自成一个连通分量。接着，每次从图G中所有两个端点落在不同连通分量的边中，选取权重最小的那条，将该边加入T中，如此往复，直至T中所有顶点都在同一个连通分量上。

注意
此处的关键点有两个：
（1）在生成最小生成树前，要对图中的所有边进行排序；
（2）如何判断一条边的两个端点是否落在不同的连通分量上：
这里可以用一个数组parent来记录每个端点在其所在连通图中的父端点（例如parent[i]表示端点i的父端点），在一个连通分量中，总有一个端点的父端点是它自己（把它看成是一棵树的根节点）。
1）开始的时候初始化该数组为parent[i]=i（因为每个端点所在的连通图只有自己）；
2）每次要判断一条边(u, v)的两个端点是否在在不同的连通分量上，就找端点u和端点v在它们所在的连通图中的最底层的父端点，具体的方法是递归地找端点k的父端点，直至某个端点的父端点等于它自己：

int find_parent(int node, int *parent) { //找端点node的最底层父端点while(parent[node] != node) {node = parent[node];}return node;
}

3）假设n=find_parent(u, parent)，m=find_parent(v, parent)，那么就要对它们进行判断：
如果n==m，说明结点u和结点v在一个连通分量上，因此不能将其加入T；
如果n!=m，说明结点u和结点v不在一个连通分量上，这时可以将(u,v)加入T，且令parent[n]=m（或parent[m]=n）。

例子
仍然以上述这个无向连通图G为例，它有5个顶点，7条边，如下图所示。
在这里插入图片描述
利用Prim算法来生成该图的最小生成树T的过程如下：
（1）先对图中的所有边按照权重递增的顺序排序：
(A, C, 1) , (B, D, 2) , (B, E, 2) , (A, D , 4) , (A, E , 4) , (A, B, 6) , (C, D, 8).
对每个端点的parent进行初始化：
parent[A] = A, parent[B] = B, parent[C] = C, parent[D] = D, parent[E] = E.

（2）从权重最短的边开始遍历：
1）(A, C, 1)，因为parent[A] != parent[C]，所以将边(A, C)加入树T，且令parent[parent[C]]=parent[A]=A.此时，parent[A] = A, parent[B] = B, parent[C] = A, parent[D] = D, parent[E] = E，此时T中有1条边。

2）(B, D, 2)，因为parent[B] != parent[D]，将边(B, D)加入树T，且令parent[parent[D]]=parent[B]=B.此时，parent[A] = A, parent[B] = B, parent[C] = A, parent[D] = B, parent[E] = E，此时T中有2条边.

3）(B, E, 2)，因为parent[B] != parent[E]，将边(B, E)加入树T，且令parent[parent[E]]=parent[B]=B.此时，parent[A] = A, parent[B] = B, parent[C] = A, parent[D] = B, parent[E] = B，此时T中有3条边

4）(A, D, 2)，因为parent[A] != parent[D]，将边(A, D)加入树T，且令parent[parent[D]]=parent[A]=A.此时，parent[A] = A, parent[B] = A, parent[C] = A, parent[D] = B, parent[E] = E，此时T中有4条边，正好等于端点数减一，因此树T生成。

2.2.2 具体实现

#define Maximum 1000
#define Biggest 100000000typedef struct EdgeListNode{int adjId;int weight;EdgeListNode* next;
};typedef struct VertexListNode{int data;EdgeListNode* firstadj;
};typedef struct GraphAdjList{int vertexnumber;int edgenumber;VertexListNode vertextlist[Maximum];
};typedef struct MiniTreeEdge {int s;int e;int weight;MiniTreeEdge *next;
};typedef struct MiniTree {MiniTreeEdge *head;int edgenumber;
};typedef struct EdgeArrayData {int l;int r;int weight;
};bool compare(EdgeArrayData a, EdgeArrayData b) {return a.weight < b.weight;
}int find_parent(int node, int *parent) {while(parent[node] != node) {node = parent[node];}return node;
}void  MiniSpanTree_Kruskal(GraphAdjList g, MiniTree *tree) {int i, j, k, edge_index, *parent;MiniTreeEdge *e;EdgeArrayData *edge = (EdgeArrayData*)malloc(sizeof(EdgeArrayData)*(g.edgenumber+2));parent = (int*)malloc(sizeof(int)*(g.vertexnumber+2));tree = (MiniTree*)malloc(sizeof(MiniTree));EdgeListNode *v;//将图中的每条边存储在edge里edge_index = 0;for(i=1; i<=g.vertexnumber; i++) {v = g.vertextlist[i].firstadj;parent[i] = i;while(v != NULL) {if(v->adjId > i) {  //为了避免将一条边存两次edge[edge_index].l = i;edge[edge_index].r = v->adjId;edge[edge_index].weight = v->weight;edge_index++;}v = v->next;}}sort(edge, edge+edge_index, compare); //将边按权重从小到大排序tree->edgenumber = 0;tree->head = NULL;for(i=0; i<edge_index; i++) {j = find_parent(edge[i].l, parent); k = find_parent(edge[i].r, parent);if(j != k) {parent[j] = k;e = (MiniTreeEdge*)malloc(sizeof(MiniTreeEdge));e->s = edge[i].l;e->e = edge[i].r;e->weight = edge[i].weight;e->next = tree->head;tree->head = e;tree->edgenumber++;}if(tree->edgenumber == g.vertexnumber - 1) {break;}}MiniTreeEdge *ee = tree->head;while(ee != NULL) {cout<<ee->s<<" -> "<<ee->e<<"  :  "<<ee->weight<<endl;ee = ee->next;}
}

2.2.3 测试

测试的图为：
在这里插入图片描述


int main() {GraphAdjList g;g.edgenumber = 5;g.vertexnumber = 4;int i, j, k;EdgeListNode *temp;for(i=1; i<=4; i++) {g.vertextlist[i].data = i;g.vertextlist[i].firstadj = NULL;}temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 2; temp->weight = 2; temp->next = g.vertextlist[1].firstadj;g.vertextlist[1].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 4; temp->weight = 8; temp->next = g.vertextlist[1].firstadj;g.vertextlist[1].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 1; temp->weight = 2; temp->next = g.vertextlist[2].firstadj;g.vertextlist[2].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 3; temp->weight = 3; temp->next = g.vertextlist[2].firstadj;g.vertextlist[2].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 4; temp->weight = 1; temp->next = g.vertextlist[2].firstadj;g.vertextlist[2].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 2; temp->weight = 3; temp->next = g.vertextlist[3].firstadj;g.vertextlist[3].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 4; temp->weight = 5; temp->next = g.vertextlist[3].firstadj;g.vertextlist[3].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 1; temp->weight = 8; temp->next = g.vertextlist[4].firstadj;g.vertextlist[4].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 2; temp->weight = 1; temp->next = g.vertextlist[4].firstadj;g.vertextlist[4].firstadj = temp;temp = (EdgeListNode*)malloc(sizeof(EdgeListNode));temp->adjId = 3; temp->weight = 5; temp->next = g.vertextlist[4].firstadj;g.vertextlist[4].firstadj = temp;MiniTree *tree;MiniSpanTree_Kruskal(g, tree);MiniTreeEdge *e = tree->head;while(e != NULL) {cout<<e->s<<" -> "<<e->e<<"  :  "<<e->weight<<endl;e = e->next;}return 0;
}