Prim 算法又称DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。

Prim 算法是一种贪心，Prim 最初的时候是将所有的点分为两个集合 $V_{a}$ 、 $V_{b}$ ，其中一个集合 $V_{a}$ 表示已经加入生成树的点，而另一个集合 $V_{b}$ 表示还未加入生成树的点。初始时， $V_{a}$ 为空(当然，也可以只包含一个节点)，其他节点都在 $V_{b}$ 。每次选从 $V_{b}$ 中选取一个节点加入 $V_{a}$ ，同时保证这一节点与 $V_{a}$ 中的某一个节点的边长最小，显然这条边就是最小生成树上的边，直到所有的节点都被插入生成树中，算法即结束，所到得的生成树就是最小生成树。

显然，这种策略是正确的。

因此，Prim 算法的时间复杂度O( $n^{2 }$ ) 。

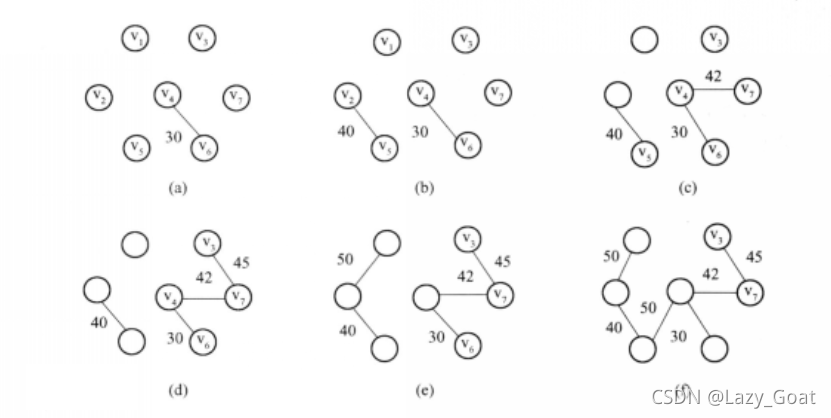
图文解释：

【代码实现】

int n;//点数 
bool v[1001];//记录该点是否被放入生成树 
int a[1001][1001];//原图数据 
int dis[1001];//每个点到生成树的距离 
for(int i=1;i<=n;i++)
{int p=0;int minn=0x7f7f7f;//初始为无穷大 for(int j=1;j<=n;j++)//寻找最短距离 {if(!v[j]&&dis[j]<minn){minn=dis[j];p=i;}}v[p]=1;ans+=minn;//加入生成树并统计边权和 for(int i=1;i<=n+1;i++)//更新每个点到生成树的最小距离 {if(dis[i]>a[p][i]){dis[i]=a[p][i];}}
}

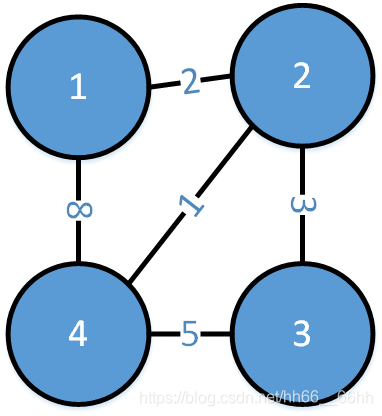
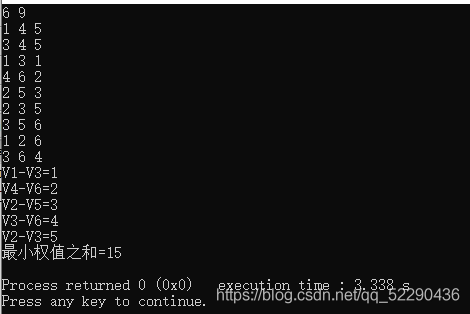
这里为大家引入一道的 Prim 算法的例题：

解题思路：目标是在一个点上建立一所发电站，并让所有的矿井都有电可用。这样一来，就可以引入一个新的知识——超级点。可以设不存在的 0 号点作为超级点，在矿井上建立发电站相当于把它与 0 号点相连，这样以来，问题就转化成了一个最小生成树问题，然后，就是套用 Prim 的模板。

【AC 代码】

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
int n,m,ans;
int minn;
int dis[2001],k;
bool v[2001];
int f[2001][2001];//变量的声明
int main()
{scanf("%d",&n);//读入for(int i=1;i<=n;i++){int x;scanf("%d",&x);//读入f[i][0]=x;//设置0号点f[0][i]=x;//设置0号点}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){scanf("%d",&f[i][j]);//读入}}for(int i=1;i<=n;i++){f[i][i]=0x7f7f7f;//自己与自己不能相连，所以初始为无穷大}v[0]=true;//0号点放入生成树for(int i=1;i<=n;i++){dis[i]=f[0][i];//初始与生成树的最小距离}for(int i=1;i<=n;i++){minn=0x7f7f7f;k=0;for(int j=1;j<=n;j++)//寻找距离最短且不在生成树上的点{if((!v[j])&&(dis[j]<minn)){minn=dis[j];k=j;}}ans+=dis[k];//加入生成树，并更新权值v[k]=true;//标记for(int j=1;j<=n;j++)//更新每个点到生成树的最短距离{if(f[k][j]<dis[j]){dis[j]=f[k][j];}}}printf("%d\n",ans);//输出return 0;//完结撒花}

kruskal 算法：

kruskal 算法也是一种贪心算法，只不过 Prim 算法是对生成树上的点所连的边贪心，而kruskal 算法是对所有的边进行贪心。

kruskal 算法的策略是：先把每个节点当成一颗最小生成树，然后按照边权从小到大排序，每次枚举边权最小的边，如果两个点不在同一棵最小生成树中，就将两棵生成树合并，反之则舍弃，直到插入 n-1 条边形成一珂生成树。得到的生成树就是最小生成树。

kruskal 算法与并查集有惊人的相似，所以建议先学会并查集。

显然，这种策略是正确的。

因此，kruskal 算法的时间复杂度是：O(m×log m) 。

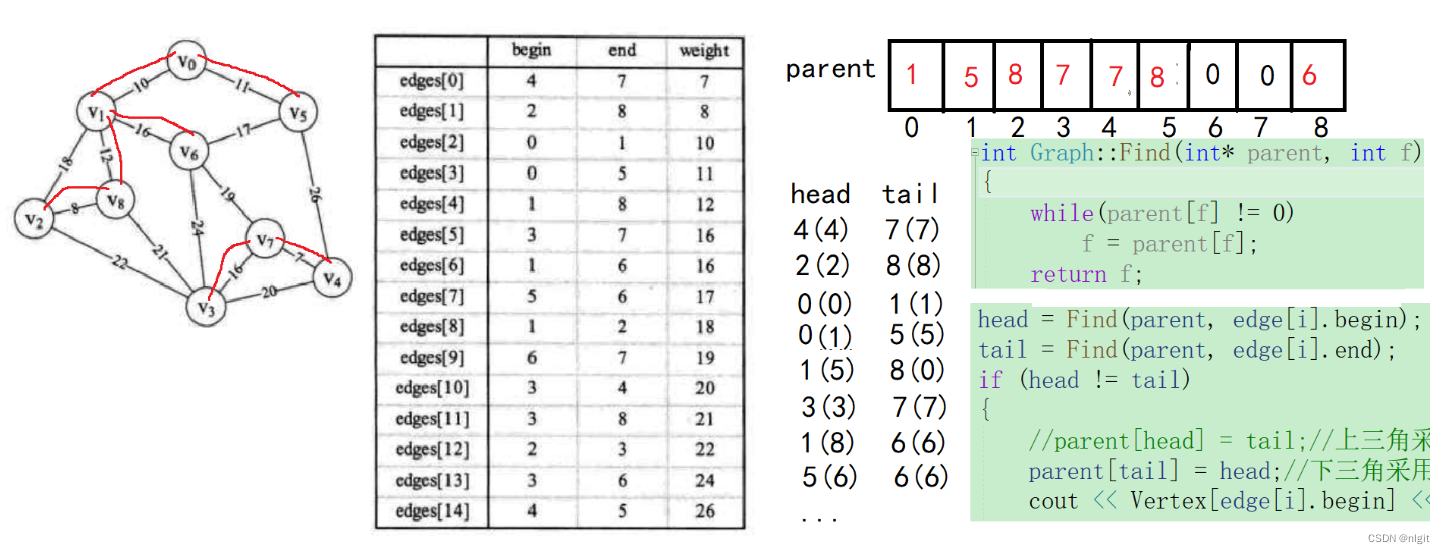
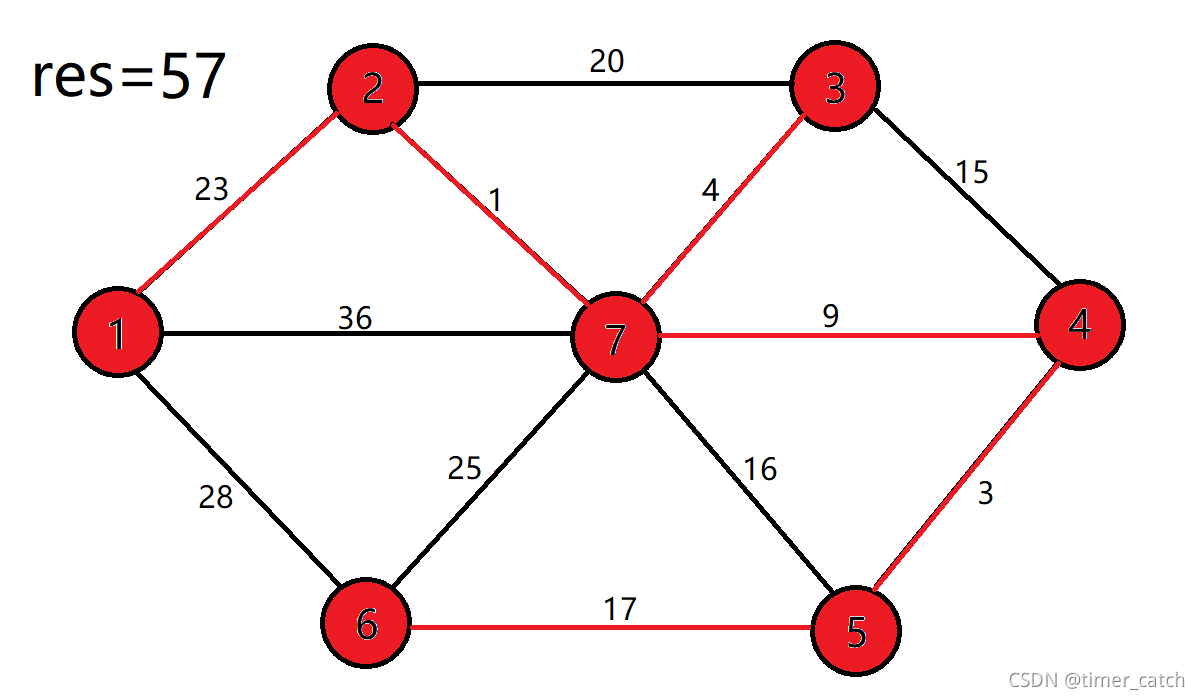
图文解释：

【代码实现】

int n,m;//n个点，m条边
int sum,ans;//sum记录连接的边数
int fa[1000001];//记录其祖先
struct node//结构体
{int x;//端点之一int y;//端点之二int w;//边权值
}a[1000001];
int cmp(node x,node y)//将数据按照从小到大的顺序排序
{return x.w<y.w;
}
int find(int k)//寻找k的祖先
{if(fa[k]==k){return k;}return fa[k]=find(fa[k]);
}
for(int i=1;i<=n;i++)//初始化
{fa[i]=i;
}
sort(a+1,a+1+m,cmp);//排序
for(int i=1;i<=m;i++)//加边
{int x=find(a[i].x);//找端点之一的祖先int y=find(a[i].y);//找端点之二的祖先if(x!=y)//如果不在同一个集合{fa[y]=x;//合并sum++;//边数加1ans+=a[i].w;//记录边权和if(sum==n-1)//如果边数达到n-1，则寻找完毕{break;/*/跳出循环}} 
}

小编为大家引入一道经典的 kruskal 的题目，以便大家巩固。

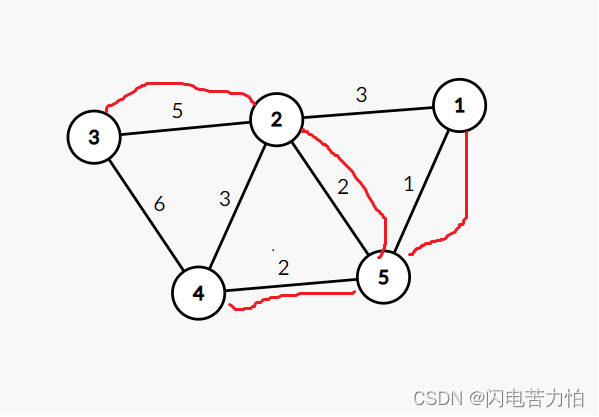
题目传送名：P2330 [SCOI2005]繁忙的都市

解题思路：其实这道题不论是用 Prim 还是 kruskal 都很简单，不过这里主要以练习 kruskal 为主要目的，所以，重点讲 kruskal 算法。

题目要求的是最少的边数和生成树内最大的边权值，边的数量肯定是 n-1 ，最大的边权值也只需要在跑 kruskal 的时候记录即可。

【代码实现】

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<vector>
#include<string>
#include<cstring>
#include<queue>//头文件
using namespace std;
int n,m;//n个点，m条边
int sum,ans;//sum用来记录加入生成树的边的数量，ans用来更新最大的边权值
int fa[1000001];//记录祖先节点
struct node//记录每条边的信息
{int x;int y;int w;//边的权值
}a[1000001];
int cmp(node x,node y)//将所有的边按照从小到大的顺序排列
{return x.w<y.w;
}
int find(int k)//寻找祖先元素
{if(fa[k]==k){return k;}return fa[k]=find(fa[k]);
}
int main()
{scanf("%d%d",&n,&m);//读入for(int i=1;i<=n;i++){fa[i]=i;//初始化}for(int i=1;i<=m;i++)//读入{int x,y,w;scanf("%d%d%d",&x,&y,&w);a[i].x=x;a[i].y=y;a[i].w=w;}sort(a+1,a+1+m,cmp);//排序for(int i=1;i<=m;i++)//枚举边{int x=find(a[i].x);//查询a[i].x的祖先int y=find(a[i].y);//查询a[i].y的祖先if(x==y)//如果已经在一个集合中，则忽略{continue;} fa[x]=y;//合并两个集合sum++;//边数累加ans=max(ans,a[i].w);//更新最大边权值if(sum==n-1)//如果生成树中的边数等于n-1，则最小生成树已经生成{break;//跳出}}printf("%d %d\n",sum,ans);//输出return 0;//完结撒花
}