概述

克鲁斯卡尔$(Kruskal)$算法是求连通网的最小生成树的另一种方法。与普里姆$(Prim)$算法不同，它的时间复杂度为$O(eloge)$(e为网中的边数)，所以，适合于求边稀疏的网的最小生成树 。

$Prim$和$Kruskal$，前者更适合顶点较多的时候使用；后者更适合边较少的时候使用；

算法分析

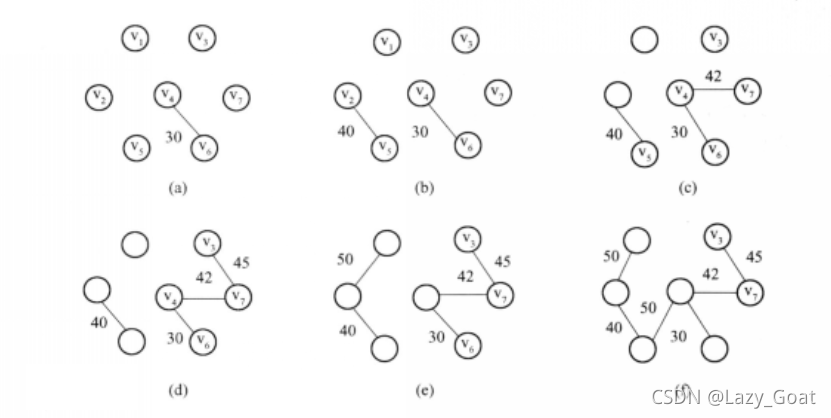
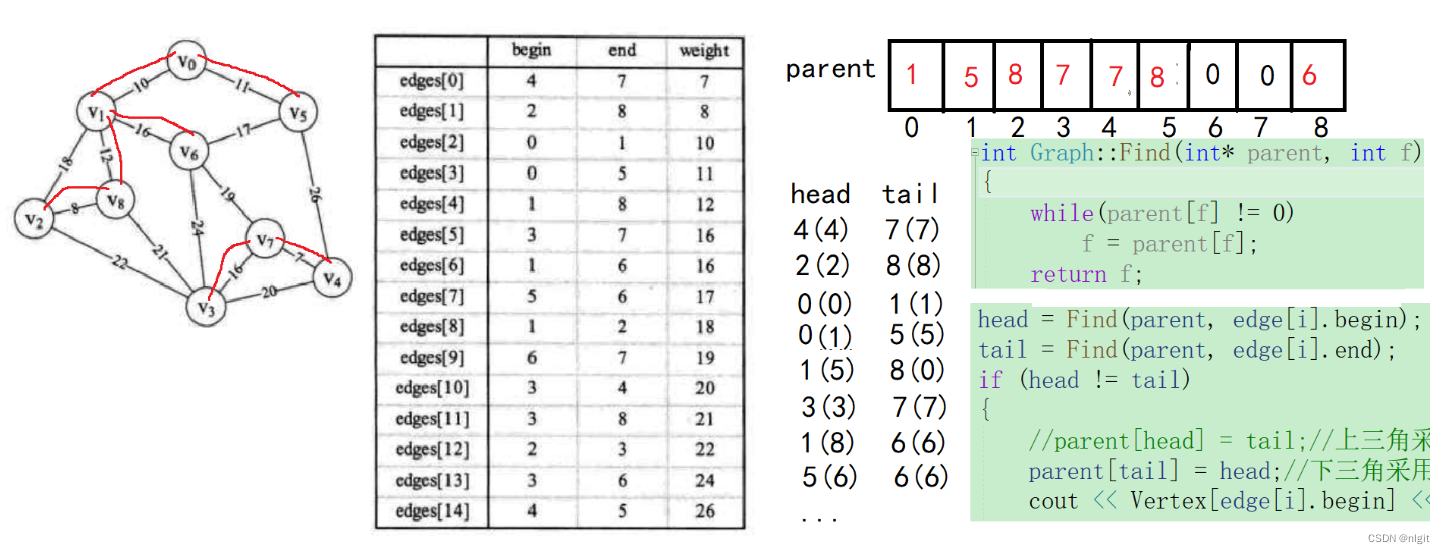
按权值由小到大的顺序排列的编辑是：（各边由起点序号，终点序号，权值表示）

1. (4,6,30)
2. (2,5,40)
3. (4,7,42)
4. (3,7,45)
5. (1,2,50)
6. (4,5,50)
7. (3,4,52)
8. (1,3,60)
9. (2,4,65)
10. (5, 6, 70)

$Kruskal$算法思想简单，但是在实现的时候需要考虑防止闭合回路的出现。

我们把属于一条边的两个顶点作为一个集合，通过这样方法就可以防止闭合回路的出现。

如果是同一条边就把两个顶点赋值相同的数值。

使用这样的结构体把数据存储起来$Edge$

typedef struct{ int vex1;  //边的起始顶点 int vex2;  //边的终止顶点 int weight; //边的权值 
}Edge;

收集好图的数据以后，使用递归排序使边以从小到大(权值的的大小)的顺序排好。

这是一个递归排序 $\downarrow$

int fun(Edge arr[],int low,int high){int key;Edge lowx;lowx=arr[low];key=arr[low].weight;while(low<high){while(low<high && arr[high].weight>=key)high--;if(low<high)arr[low++]=arr[high];while(low<high && arr[low].weight<=key)low++;if(low<high)arr[high--]=arr[low];}arr[low]=lowx;return low;} 
void quick_sort(Edge arr[],int start,int end)
{int pos;if(start<end){pos=fun(arr,start,end);quick_sort(arr,start,pos-1);quick_sort(arr,pos+1,end);}
}

调用$Kruskal$算法生成最小树

void kruskal(Edge E[],int n,int e)
{ int i,j,m1,m2,sn1,sn2,k,sum=0;int vset[n+1];for(i=1;i<=n;i++) //初始化辅助数组 vset[i]=i;k=1;//表示当前构造最小生成树的第k条边，初值为1 j=0;//E(边集)中边的下标，初值为0while(k<e)//生成的边数小于e时继续循环 {m1=E[j].vex1;m2=E[j].vex2;//取一条边的两个邻接点 sn1=vset[m1];sn2=vset[m2];                           //分别得到两个顶点所属的集合编号 if(sn1!=sn2)//两顶点分属于不同的集合，该边是最小生成树的一条边  {//防止出现闭合回路 printf("V%d-V%d=%d\n",m1,m2,E[j].weight);sum+=E[j].weight;k++;   //生成边数增加 if(k>=n)break;for(i=1;i<=n;i++)    //两个集合统一编号if (vset[i]==sn2)  //集合编号为sn2的改为sn1vset[i]=sn1;}j++;//扫描下一条边 }printf("最小权值之和=%d\n",sum);
}

这个算法中，这部分做的是初始化工作。

	int i,j,m1,m2,sn1,sn2,k,sum=0;int vset[n+1];for(i=1;i<=n;i++) //初始化辅助数组 vset[i]=i;k=1;//表示当前构造最小生成树的第k条边，初值为1 j=0;//E(边集)中边的下标，初值为0

$vest[]$数组用于判断两个顶点是否属于同一个集合。

以权值从小到大的顺序取出每一条边(两个顶点和权值)，判断这个边两顶点是否属于同一个集合。如果属于，则取下一条边；否则记录这条最小边，然后统一这条边的两个顶点所属的集合。

   while(k<e)//生成的边数小于e时继续循环 {m1=E[j].vex1;m2=E[j].vex2;//取一条边的两个邻接点 sn1=vset[m1];sn2=vset[m2];                           //分别得到两个顶点所属的集合编号 if(sn1!=sn2)//两顶点分属于不同的集合，该边是最小生成树的一条边  {//防止出现闭合回路 printf("V%d-V%d=%d\n",m1,m2,E[j].weight);sum+=E[j].weight;k++;//生成边数增加 if(k>=n)break;for(i=1;i<=n;i++)    //两个集合统一编号if (vset[i]==sn2)  //集合编号为sn2的改为sn1vset[i]=sn1;}j++;//扫描下一条边 }

代码

#include <stdio.h>
#define MAXE 100
#define MAXV 100
typedef struct{ int vex1;  //边的起始顶点 int vex2;  //边的终止顶点 int weight; //边的权值 
}Edge;
void kruskal(Edge E[],int n,int e)
{ int i,j,m1,m2,sn1,sn2,k,sum=0;int vset[n+1];for(i=1;i<=n;i++) //初始化辅助数组 vset[i]=i;k=1;//表示当前构造最小生成树的第k条边，初值为1 j=0;//E(边集)中边的下标，初值为0while(k<e)//生成的边数小于e时继续循环 {m1=E[j].vex1;m2=E[j].vex2;//取一条边的两个邻接点 sn1=vset[m1];sn2=vset[m2];                           //分别得到两个顶点所属的集合编号 if(sn1!=sn2)//两顶点分属于不同的集合，该边是最小生成树的一条边  {//防止出现闭合回路 printf("V%d-V%d=%d\n",m1,m2,E[j].weight);sum+=E[j].weight;k++;   //生成边数增加 if(k>=n)break;for(i=1;i<=n;i++)    //两个集合统一编号if (vset[i]==sn2)  //集合编号为sn2的改为sn1vset[i]=sn1;}j++;//扫描下一条边 }printf("最小权值之和=%d\n",sum);
}
int fun(Edge arr[],int low,int high){int key;Edge lowx;lowx=arr[low];key=arr[low].weight;while(low<high){while(low<high && arr[high].weight>=key)high--;if(low<high)arr[low++]=arr[high];while(low<high && arr[low].weight<=key)low++;if(low<high)arr[high--]=arr[low];}arr[low]=lowx;return low;} 
void quick_sort(Edge arr[],int start,int end)
{int pos;if(start<end){pos=fun(arr,start,end);quick_sort(arr,start,pos-1);quick_sort(arr,pos+1,end);}
}
int main()
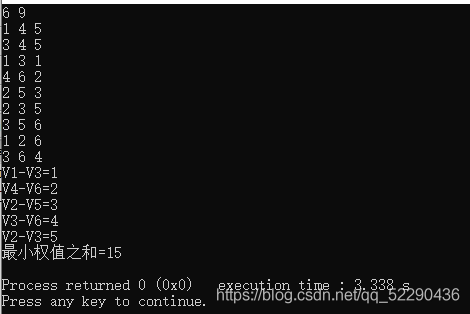
{Edge E[MAXE];int nume,numn;printf("输入顶数和边数:\n");scanf("%d%d",&numn,&nume);for(int i=0;i<nume;i++)scanf("%d%d%d",&E[i].vex1,&E[i].vex2,&E[i].weight);quick_sort(E,0,nume-1);kruskal(E,numn,nume);
}
//INPUT要输入的：
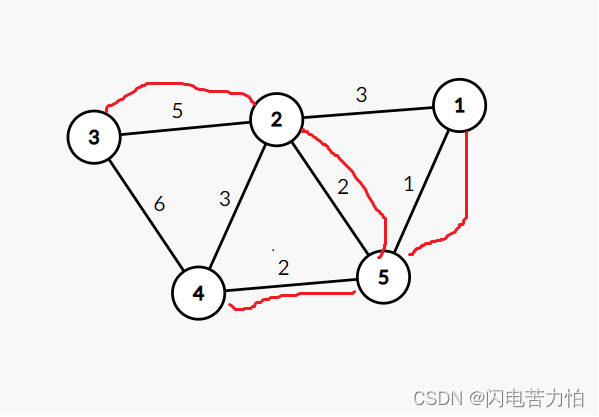
//6 10
//1 2 6
//1 3 1
//1 4 5
//2 3 5
//2 5 3
//3 4 5
//3 5 6
//3 6 4
//4 6 2
//5 6 6