最小生成树

本文参考自《大话数据结构》

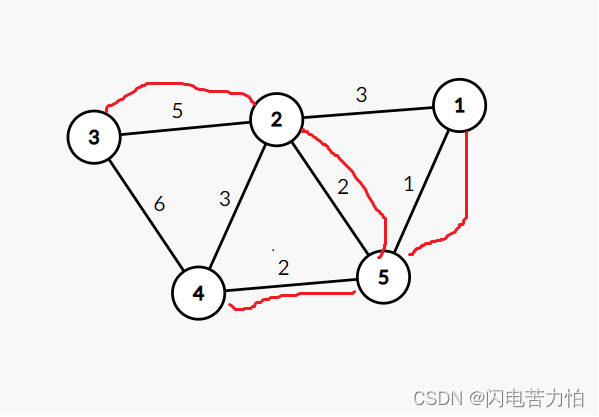
一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树称为最小生成树 。

找连通网的最小生成树，经典的有两种算法：普里姆算法和克鲁斯卡尔算法。

普里姆(Prim)算法

/* Prim算法生成最小生成树 */
void MiniSpanTree_Prim(MGraph G){int min, i, j, k;int adjvex[MAXVEX];	//保存相关顶点下标int lowcost[MAXVEX];	//保存相关顶点间边的权值lowcast[0] = 0;	//初始化第一个权值为0，即v0加入生成树，lowcost的值为0，在这里就是此下标的顶点已经加入生成树adjvex[0] = 0;	//初始化第一个顶点下标为0for(i = 1;i<G.numVertexes;i++){	//循环除下标为0外的全部顶点lowcost[i] = G.arc[0][i];		//将v0顶点与之有边的权值存入数组adjvex[i] = 0;	//初始化都为v0的下标}for(i=1;i<G.numVertexes;i++){min = INFINITY;	//初始化最小权值为无穷大，通常设置为很大的数字j = 1;k = 0;while(j<G.numVertexes){		//循环全部顶点if(lowcost[j] != 0 && lowcost[j] < min){	//如果权值不为0且权值小于minmin = lowcost[j];		//让当前权值成为最小值k = j;		//将当前最小值的下标存入k}j++;}printf("(%d,%d)",adjvex[k],k);	//打印当前顶点边中权值最小边lowcost[k] = 0;	//将当前顶点的权值设置为0，表示此顶点已经完成任务for(j=1;j<G.numVertexes;j++){	//循环所有顶点if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j]){	//若下标为k顶点各边权值小于此前这些顶点未被加入生成树权值lowcost[j] = G.arc[k][j];		//将较小权值存入lowcostadjvex[j] = k;	//将下标为k的顶点存入adjvex}}}
}

假设N=(P,{E})是连通网，TE是N上最小生成树中边的集合。算法从U={u0}（u0∈V），TE={}开始。重复执行下述操作：在所有u∈U，v∈V-U的边（u，v）∈E中找一条代价最小的边（u0，v0）并入集合TE，同时v0并入U，直至U=V为止。此时TE中必有n-1条边，则T=(V,{TE})为N的最小生成树。

由算法代码中的循环嵌套可得此算法复杂度为O(n^2)。

克鲁斯卡尔(Kruskal)算法

普里姆算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树的。
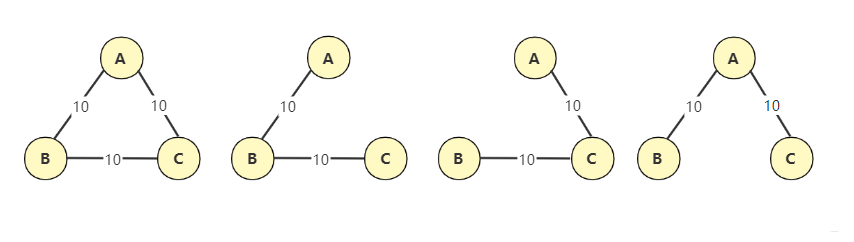
而克鲁斯卡尔算法是以边为目标进行构建，因为权值是在边上，直接去找最小值的边来构建生成树也是很自然的想法，只不过构建时要考虑是否会形成环路而已。

edge边集数组结构的定义代码：

/* 对边集数组Edge结构的定义 */
typedef struct{int begin;int end;int weight;
}Edge;

克鲁斯卡尔算法代码如下：

/* kruskal算法生成最小生成树 */
void MiniSpanTree(MGraph G){	//生成最小生成树int i, n, m;Edge edges[MAXEDGE];	//定义边集数组int parent[MAXVEX];	//定义一数组用来判断边与边是否形成环路/* 此处省略将邻接矩阵G转化为边集数组edges并按权由小到大排序的代码 */for(i = 0;i<G.numVertexes;i++)parent[i] = 0;	//初始化数组值为0for(i = 0;i<G.numEdges;i++){	//循环每一条边n = Find(parent, edges[i].begin);m = Find(parent, edges[i].end);if(n != m){		//假如n与m不等，说明此边没有与现有生成树形成环路parent[n] = m;	//将此边的结尾顶点放入下标为起点的parent中，表示此顶点已经在生成树集合中printf("(%d,%d) %d", edges[i].begin, edges[i].end, edges[i].weight);}}
}int Find(int* parent, int f){	//查找连线顶点的尾部下标while(parent[f] > 0)f = parent[f];return f;
}

克鲁斯卡尔算法实现的定义：

假设N={V,{E})是连通网，则令最小生成树的初始状态为只有n个顶点而无边的非连通图T={V,{}}，图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连同分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。以此类推，直到T中所有顶点都在同一连通分量上为止。
此算法的Find函数由边数e决定，时间复杂度为O(loge)，而外面有一个for循环e次，所以克鲁斯卡尔算法的时间复杂度为O(eloge)。
对比两个算法，克鲁斯卡尔算法主要是针对边展开，边数少的时候效率会非常高，所以对于稀疏图有很大的优势；而普里姆算法对于边数非常多的稠密图情况会更好一些。

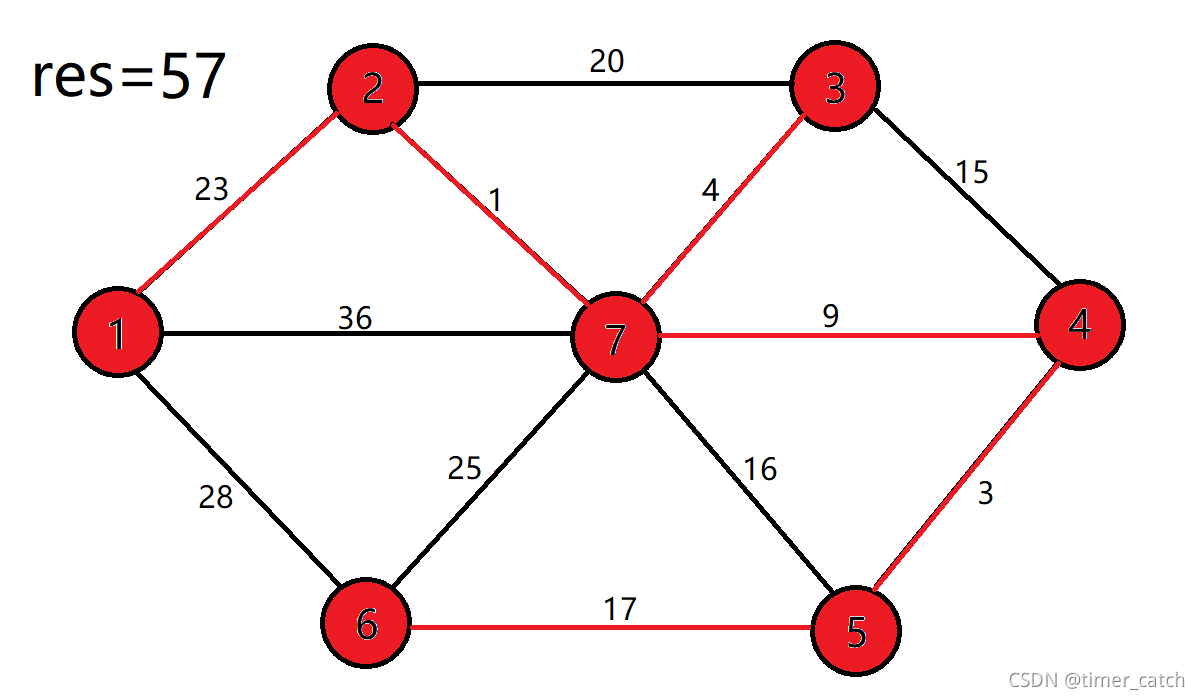
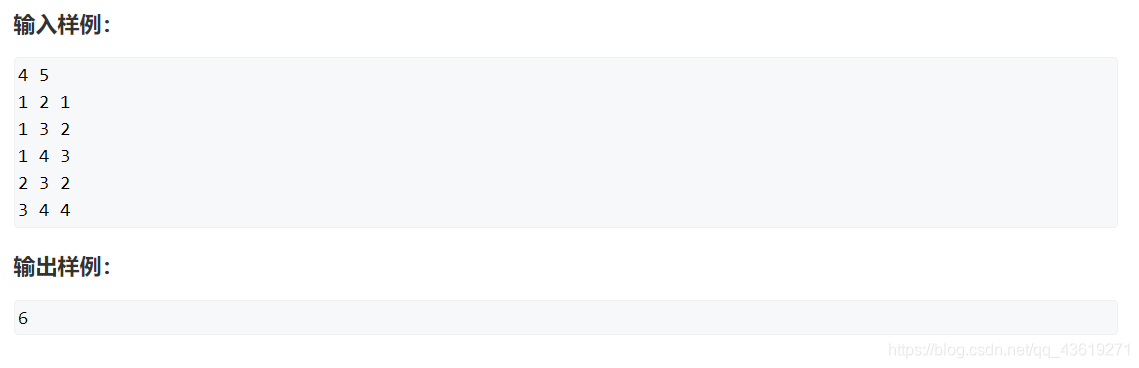
例子

最小生成树例子图解

克鲁斯卡尔

#include <stdio.h>typedef char VertexType;
typedef int EdgeType;struct Edge{int begin;int end;EdgeType weight;
};/* 插入排序 */
void sort(Edge* edge, int maxedge){int i, j, min;Edge temp;for(i=0;i<maxedge-1;i++){min = i;for(j=i+1;j<maxedge;j++){if(edge[min].weight > edge[j].weight){min = j;}}if(min != i){temp.begin = edge[i].begin;temp.end = edge[i].end;temp.weight = edge[i].weight;edge[i].begin = edge[min].begin;edge[i].end = edge[min].end;edge[i].weight = edge[min].weight;edge[min].begin = temp.begin;edge[min].end = temp.end;edge[min].weight = temp.weight;}}
}int Find(int* parent, int i){while(parent[i] > 0)i = parent[i];return i;
}/* kruskal算法生成最小生成树 */
void MiniSpanTree(int maxvex, int maxedge){int i, n, m;Edge edge[maxedge];	//定义边集数组 int parent[maxvex];	//定义一数组判断是否形成回路//===============================================此处省略了构建图的过程，图的构建可以看看我其他博客 printf("输入边和权值：\n");for(i=0;i<maxedge;i++)scanf("%d,%d,%d",&edge[i].begin, &edge[i].end, &edge[i].weight);//===============================================sort(edge, maxedge);for(i=0;i<maxvex;i++)parent[i] = 0;	//初始化for(i=0;i<maxedge;i++){n = Find(parent, edge[i].begin);m = Find(parent, edge[i].end);if(n != m){	//不等，说明没有生成环形树 parent[n] = m;	//将此边的结尾顶点放入下标为起点的parent中，表示此顶点已经在生成树集合中printf("(%d,%d)%d\n",edge[i].begin, edge[i].end, edge[i].weight); }}
}int main(){int maxvex;int maxedge;printf("输入顶点数和边数：\n");scanf("%d,%d",&maxvex, &maxedge);MiniSpanTree(maxvex,maxedge);return 0;
}

最小生成树-克鲁斯卡尔

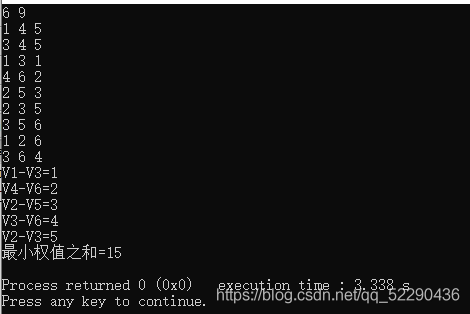
普里姆

#include <stdio.h>
#include <stdlib.h>typedef char VertexType;	//顶点类型
typedef int EdgeType;	//边上的权值类型
#define MAXVEX 100	//最大顶点数 
#define INFINITY 65535	//代表无穷大
bool visited[MAXVEX];	//标记结点是否遍历过 struct MGraph{VertexType vexs[MAXVEX];	//顶点表EdgeType arc[MAXVEX][MAXVEX];	//邻接矩阵，边表int numVertexes, numEdges;	//图中顶点数和边数 
};/* 建立无向图的邻接矩阵表示 */
void CreateMGraph(MGraph* G){int i, j, k, w;printf("输入顶点数和边数：\n");scanf("%d,%d",&G->numVertexes, &G->numEdges);printf("输入顶点值（字符）：\n");for(i=0;i<G->numVertexes;i++){//读取顶点信息，建立顶点表 getchar();	//吃掉回车 scanf("%c", &G->vexs[i]);}for(i=0;i<G->numVertexes;i++)for(j=0;j<G->numVertexes;j++)G->arc[i][j] = INFINITY;	//邻接矩阵初始化for(k=0;k<G->numEdges;k++){	//读取numEdges条边，建立邻接矩阵 printf("输入边（vi,vj）上的下标i，下标j和权w：\n");scanf("%d,%d,%d",&i,&j,&w);G->arc[i][j] = w;G->arc[j][i] = G->arc[i][j];	//无向图的邻接矩阵关于主对角线对称 }
}/* Prim算法生成最小生成树 */
void MiniSpanTree_Prim(MGraph* G){int min, i, j, k;int adjvex[MAXVEX];	//保存相关顶点下标int lowcost[MAXVEX];	//保存相关顶点间边的权值lowcost[0] = 0;	//初始化第一个权值为0，即v0加入生成树，lowcost的值为0，在这里就是此下标的顶点已经加入生成树adjvex[0] = 0;	//初始化第一个顶点下标为0for(i = 1;i<G->numVertexes;i++){	//循环除下标为0外的全部顶点lowcost[i] = G->arc[0][i];		//将v0顶点与之有边的权值存入数组adjvex[i] = 0;	//初始化都为v0的下标}for(i=1;i<G->numVertexes;i++){min = INFINITY;	//初始化最小权值为无穷大，通常设置为很大的数字j = 1;k = 0;while(j<G->numVertexes){		//循环全部顶点if(lowcost[j] != 0 && lowcost[j] < min){	//如果权值不为0且权值小于minmin = lowcost[j];		//让当前权值成为最小值k = j;		//将当前最小值的下标存入k}j++;}printf("(%d,%d)%d\n",adjvex[k],k,lowcost[k]);	//打印当前顶点边中权值最小边lowcost[k] = 0;	//将当前顶点的权值设置为0，表示此顶点已经完成任务for(j=1;j<G->numVertexes;j++){	//循环所有顶点if(lowcost[j] != 0 && G->arc[k][j] < lowcost[j]){	//若下标为k顶点各边权值小于此前这些顶点未被加入生成树权值lowcost[j] = G->arc[k][j];		//将较小权值存入lowcostadjvex[j] = k;	//将下标为k的顶点存入adjvex}}}
}int main(){MGraph* G = (MGraph*)malloc(sizeof(MGraph));CreateMGraph(G);MiniSpanTree_Prim(G);return 0;
}