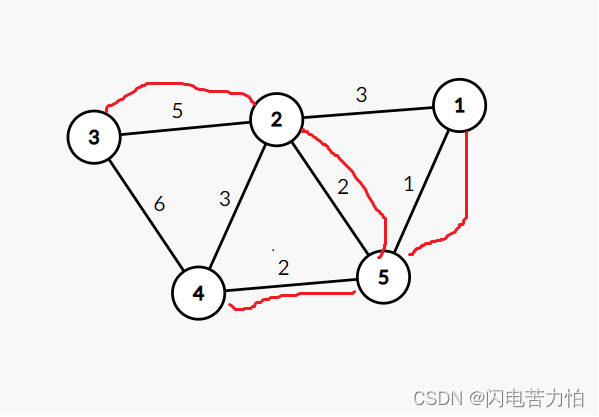
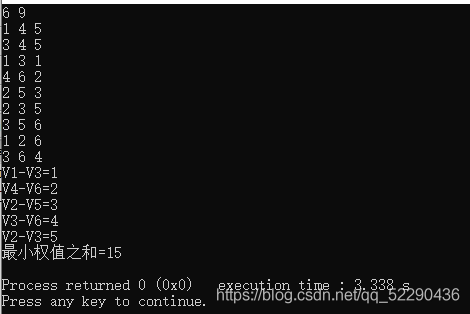
上篇Prim算法简要的讲解了最小生成树。也提到过Prim算法堆优化，但本蒟蒻并没有贴Prim         （堆优化的代码）。至于为什么没有贴呢？上篇Prim算法blog末尾有说明。

好勒！咱们接着讲Kruskal算法。这跟Prim算法有很大的不同

Prim和Kruskal算法差异：

1:Prim复杂度为O（n^2+m)   而Kruskal的复杂度为O(mlogm)    //注：n：点数    m：边数

2:Prim算法思想是枚举点的联通情况进行延伸计算，因此枚举每个点造成了n^2的复杂度，而Kruskal的算法思想是枚举边的情况，之大大减少了枚举的数量且减少了复杂度

Kruskal基本思想：

克鲁斯卡尔（Kruskal）算法从另一途径求网的最小生成树。其基本思想是：假设连通网G=（V，E），令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，{}），概述图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止。

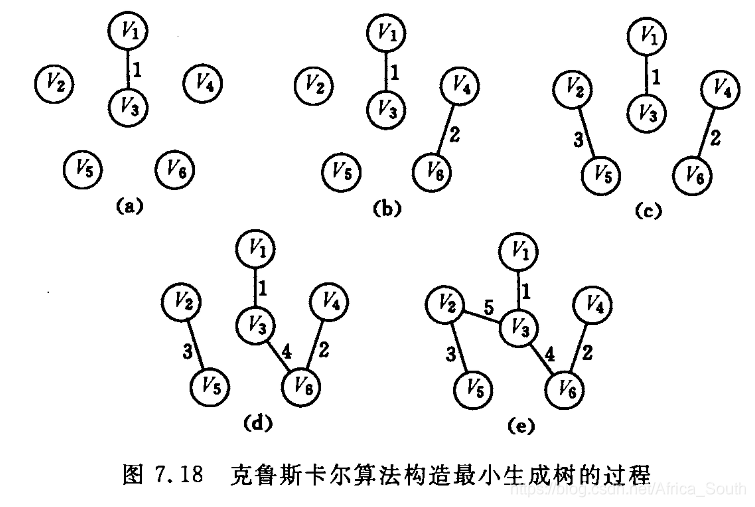
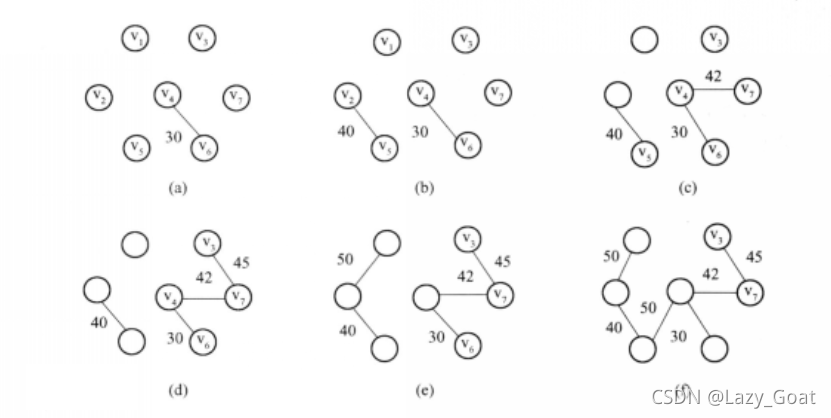
Kruskal方法构造最小生成树的过程图解：

 

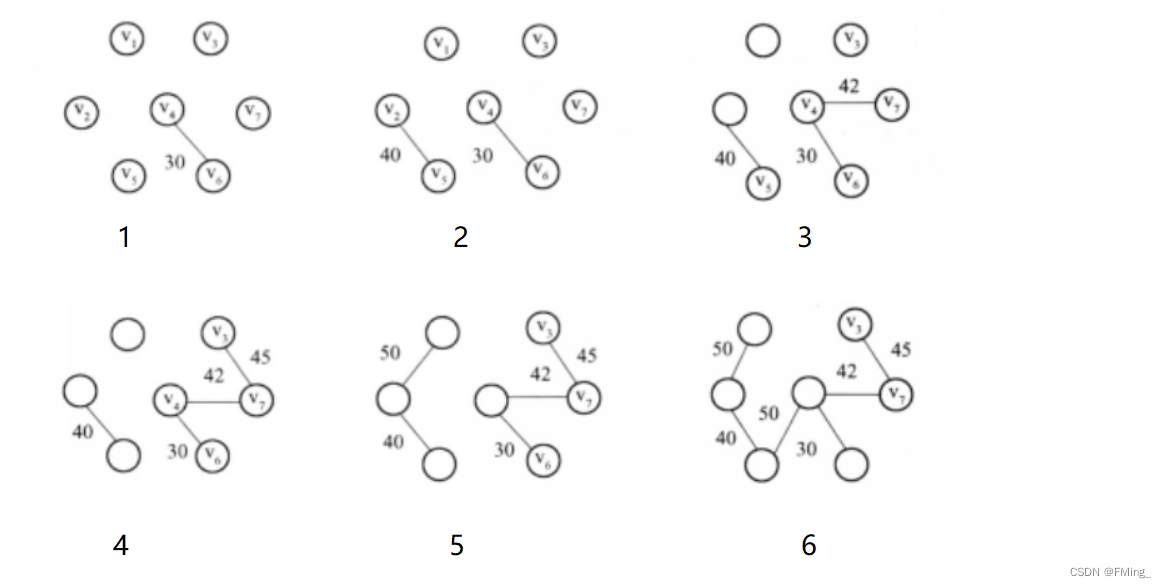
按权值由小到大的顺序排列的编辑是：（各边由起点序号，终点序号，权值表示） 

1.(4,6,30)   2.(2,5,40)   3.(4,7,42)   4.(3,7,45)   5.(1,2,50)   6.(4,5,50)   7.(3,4,52)   8.(1,3,60)

9.(2,4,65)  10.(5, 6, 70)

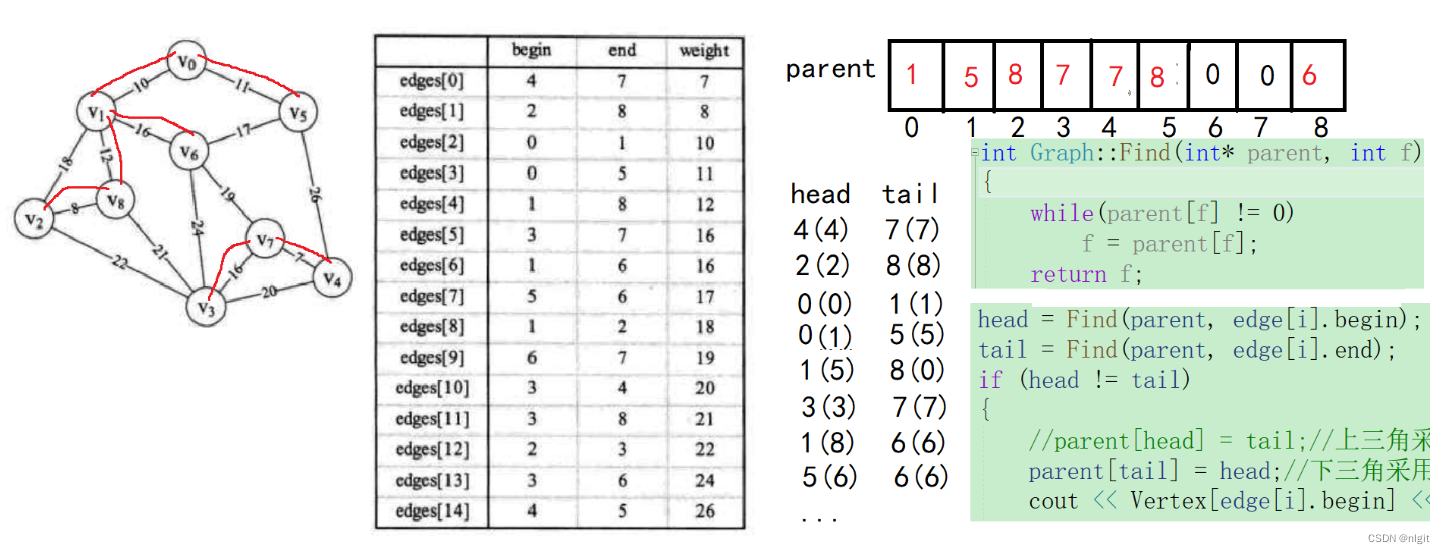
克鲁斯卡尔算法思想设计克鲁斯卡尔算法函数主要包括两个部分：首先是带权图G中e条边的权值的排序；其次是判断新选取的边的两个顶点是否属于同一个连通分量。对带权图G中e条边的权值的排序方法可以有很多种，各自的时间复杂度均不相同，对e条边的权值排序算法时间复杂度较好的算法有快速排序法、堆排序法等，这些排序算法的时间复杂度均可以达到O（elge）。判断新选取的边的两个顶点是否属于同一个连通分量的问题是一个在最多有n个顶点的生成树中遍历寻找新选取的边的两个顶点是否存在的问题，此算法的时间复杂度最坏情况下为O（n）

观察Kruskal算法：

无向连通网的最小生成树首先是一棵生成树，即它应该是一个使网中所有顶点相连通而所需边的条数为最小的子网络，且其代价和在所有生成树中为最小。因此，可以从网的连通性角度来观察Kruskal算法。

初始时，最小生成树就是网中所有顶点的集合，它们之间没有任何一条边连接，即它们自成一个连通分量。而Kruskal算法的执行过程其实就是一个选取网中权值为最小的边的过程，即将两个小的连通分量连接为较大的连通分量，直至所有顶点都在一个连通分量中为止。每当选取网中的一条边时总会出现以下两种情况之一： 

①该边所依附的两个顶点分属于不同的连通分量。这时，该边可以作为最小生成树的一条边，因为两个不同的连通分量通过这条边的连接而相连通，成为了一个连通分量 。

②该边所依附的两个顶点属于同一个连通分量。如果选取这条边作为最小生成树的一条边，则必将构成环。因为连通分量中任意两个顶点间都有路径相通，一旦再加入一条边，该边所依附的两个顶点之间就有了两条路径，即构成了环。故属于这种情况的边即使其权值小也应该舍弃

再结合例题＋代码的方式进行讲解：

小二，上题！

例题：链接：http://oj.daimayuan.top/course/14/problem/691

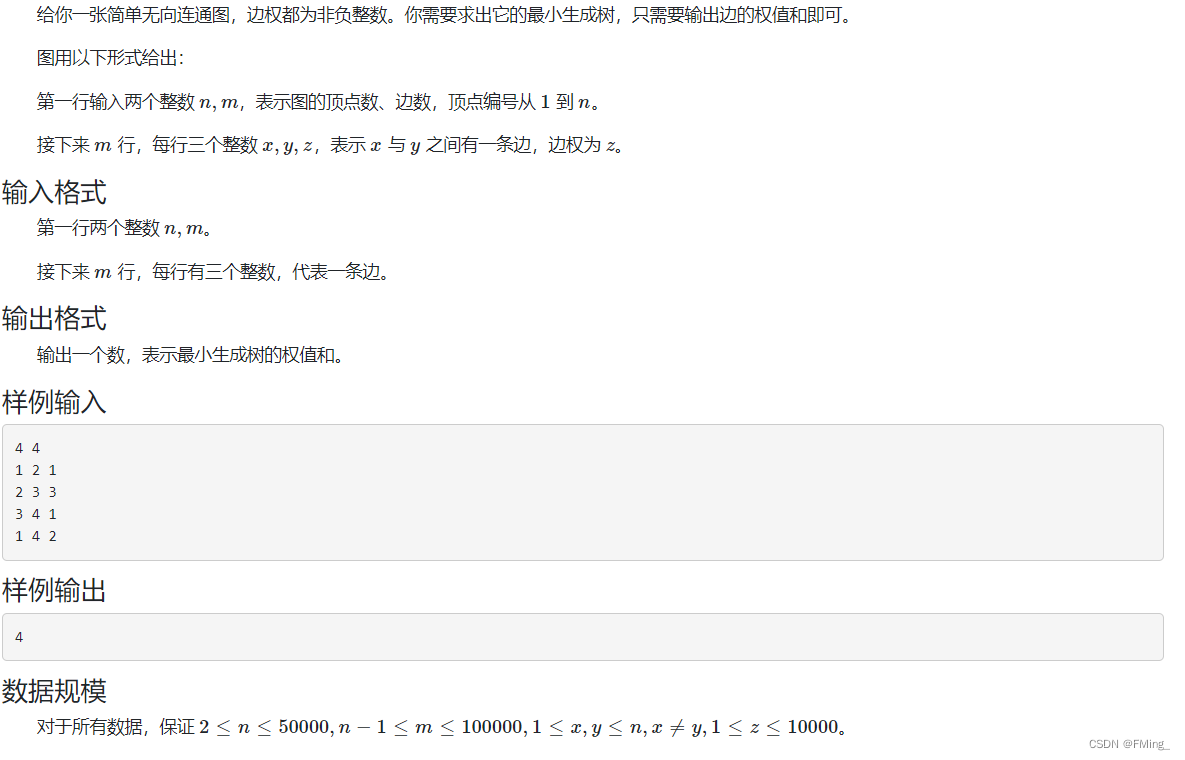
代码实现：

//Kruskal算法：O(mlogm): m为边的数量
#include<bits/stdc++.h>//万能头文件
using namespace std;
const int M=100002;//边的数量
const int N=50001;//点的数量
struct Node//定义一个包含起点，终点，边权的结构体
{int x,y,v;bool operator<(const Node &A) const//重构//目的是进行边权由小到排序{return v<A.v;}
}a[M];int n,m,fa[N];
//并查集的基本操作，在数据结构专题里我有讲解，大佬们要是忘记了，可以去看看
int Find(int x)//找父节点
{if(x==fa[x]) return x;return fa[x]=Find(fa[x]);
}
//Kruskal算法
int Kruskal()
{for(int i=1;i<=n;i++) fa[i]=i;//初始化父节点sort(a+1,a+1+m);//将边权排序int ans=0,cnt=n;//ans记录最小生成树的值，cnt代表有多少个集合for(int i=1;i<=m;i++)//枚举边{int x=Find(a[i].x),y=Find(a[i].y);//找起点和终点所属的集合if(x!=y)//若是不在一个集合（父节点）{fa[x]=y;//进行合并操作ans+=a[i].v;//加最小边权--cnt;//总集合树-1}if(cnt==1) break;//如果最终只有一个集合，说明已经生成了最小生成树，就结束循环}if(cnt!=1) return -1;//如果不为一个集合，返回-1else return ans;//否则返回最小生成树值
}int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=m;i++)//存图操作scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].v);printf("%d",Kruskal());
}

总结：

1.最小生成树的算法分为两种： Prim算法和Kruskal（本蒟蒻目前就只知道这两种）

2.Prim是在点上的操作，Kruskal是在边上的操作

3.Prim算法复杂度：O(n^2+m)               Prim（堆优化）:O((m+n)logn) 

   Kruskal算法复杂度：O(mlogm)

来都来了，给个点赞和关注呗（路过的给本蒟蒻一个赞也行...QAQ）