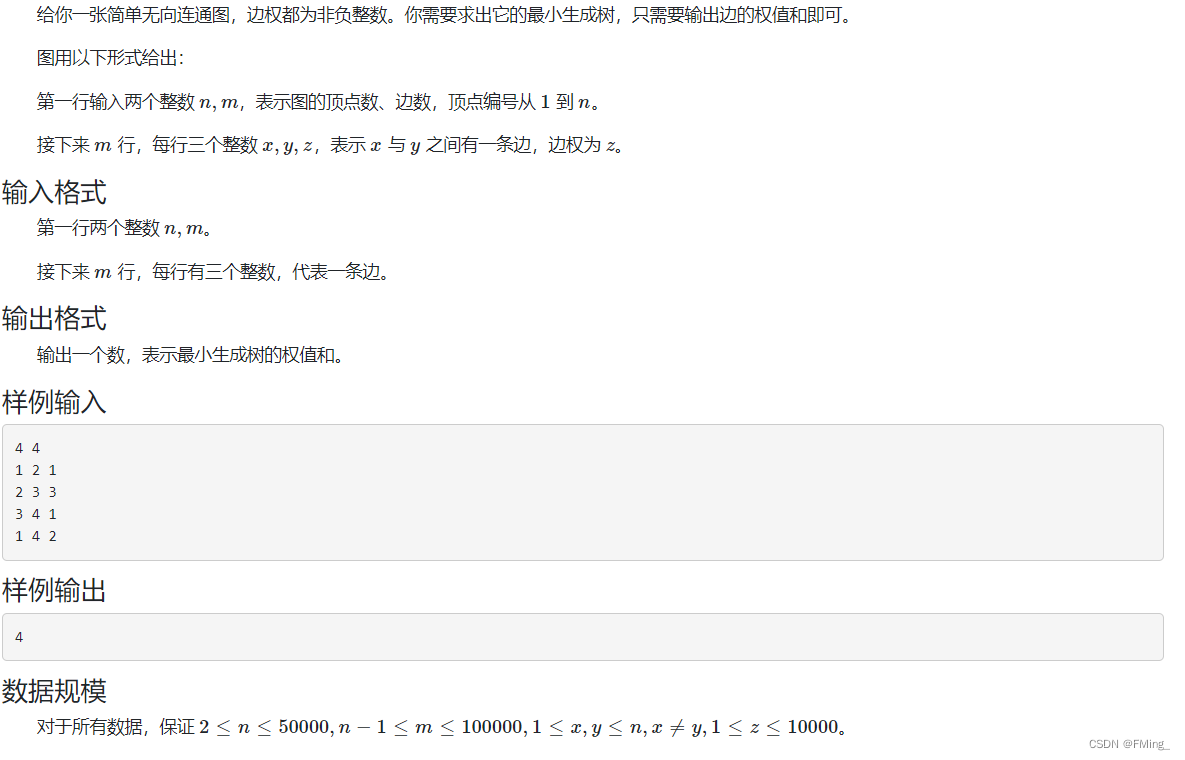
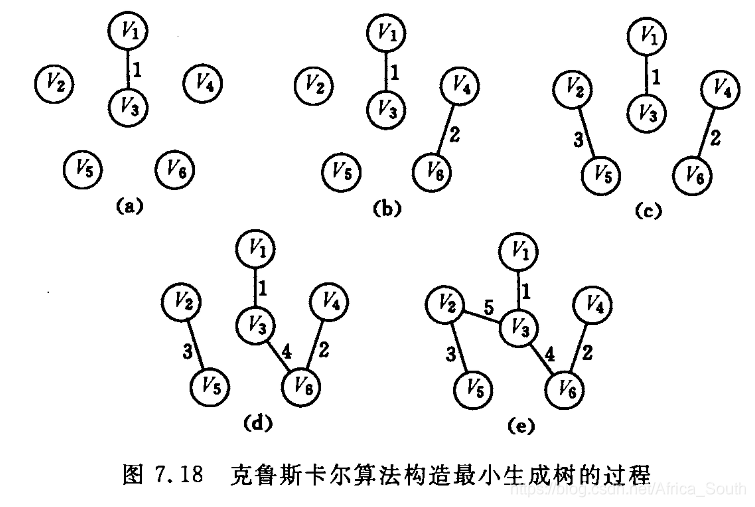
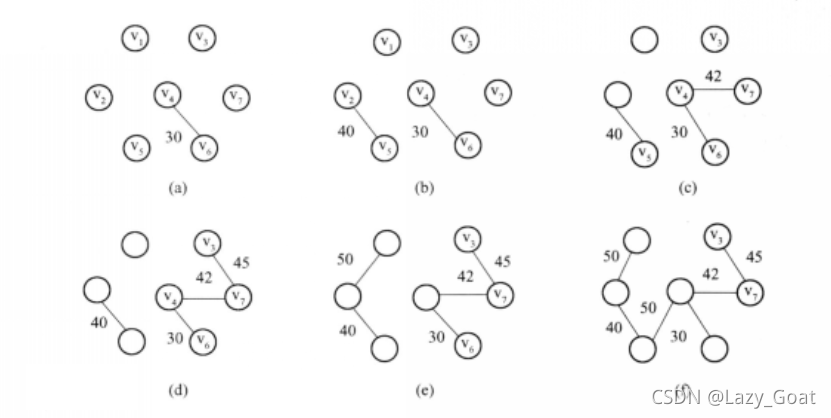
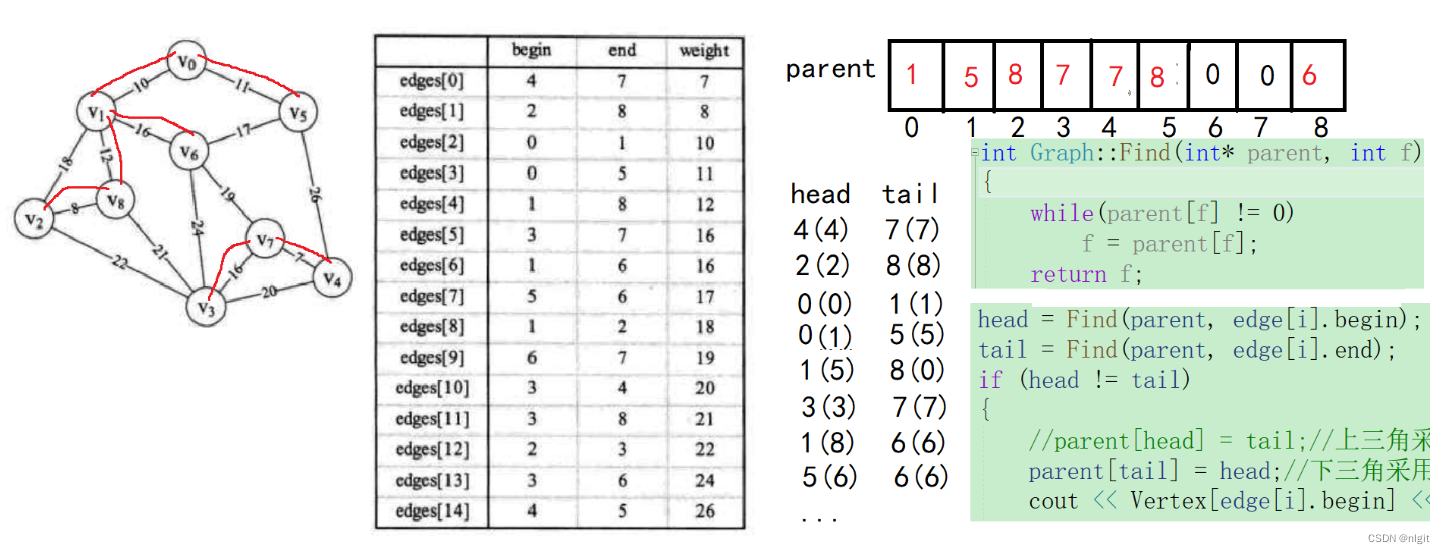
最小树形图（有向图的最小生成树）

article/2025/9/16 9:41:39

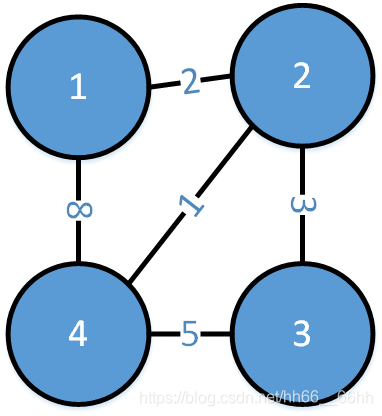
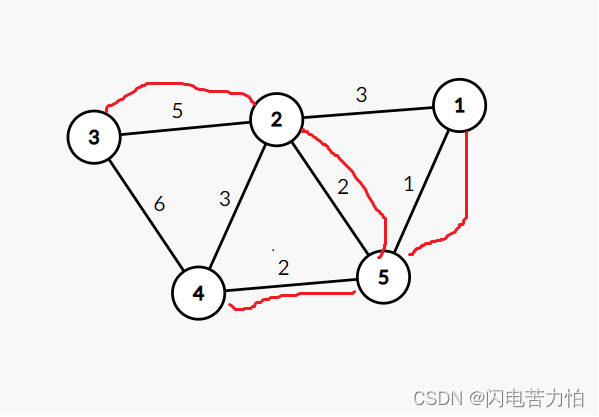
我们知道，无向图的最小生成树的求法有Krusal和prime算法，一个是归点一个是归边，在具体实现上Krusal可以用并查集实现，难度不大。

这里稍微区别一下最短路径和最小生成树（因为我又搞混了23333）
最小生成树能够保证首先是树（对于n个顶点的图只有n-1条边），其次保证任意两个顶点之间都可达，再次保证这棵树的边权值之和为最小，但不能保证任意两点之间是最短路径；
最短路径保证从源点S到目地点D的路径最小（有向图中不要求终点能到起点），不保证任意两个顶点都可达;
最小生成树是用最小代价遍历整个图中所有顶点，所有的权值和最小。而最短路径只是保证出发点到终点的路径和最小，不一定要经过所有顶点；
最小生成树是到一群点（所有点）的路径代价和最小，是一个n-1条边的树，最短路径是从一个点到另一个点的最短路径；
总之，最小生成树一定保证包含所有结点，而最短路径则不然。若题目要求必须每个点都必须经过，则是MST的问题；若只要求起点终点的最小消费，则是最短路径问题。

那么，对于有向图求最小生成树应该如何求呢？有向图就意味着可能有环，比如下面的图：
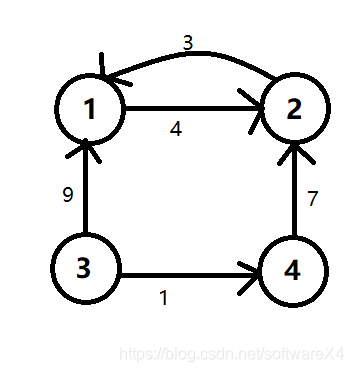
在这里插入图片描述
1、2结点形成一个环，应该删除哪一条边呢？如果从3出发，就会删掉2->1的边，如果从4出发，就会删掉1->2的边。那么如果把1、2合成一个点，所以3的权值更新为9-3=6，同理4的权值变为7-4 = 3。相当于变相删除不需要走的边。
有向图的最小生成树（最小树形图）求解步骤如下：

先求出最短弧集合E0；

对于节点1 = min{3,9},结点2 = min{4,7},结点4 = 1

如果E0不存在，则图的最小树形图也不存在；
如果E0存在且不具有环，则E0就是最小树形图；
如果E0存在但是存在有向环，则把这个环收缩成一个点u，形成新的图G1，然后对G1继续求其的最小树形图，直到求到图Gi，如果Gi不具有最小树形图，那么此图不存在最小树形图，如果Gi存在最小树形图，那么逐层展开，就得到了原图的最小树形图。

对于上面那张图，整个过程直观地看就是这样：
收缩环
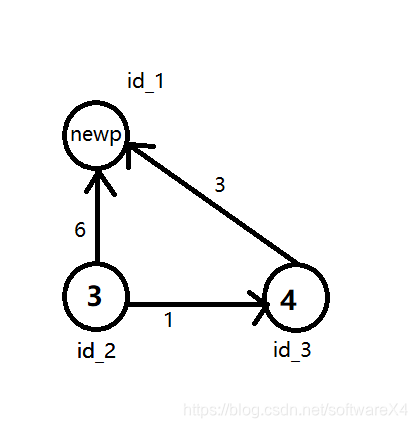
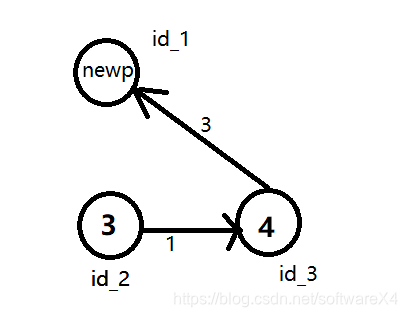
收缩之后的最小树形图
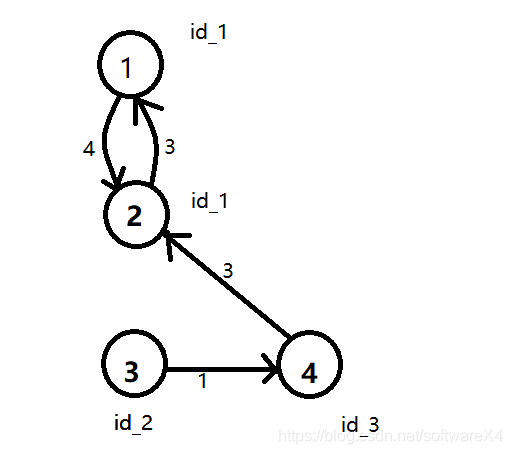
展开收缩点如下，则权值和为1+3+3+4=11
下面是一个更科学的流程图：
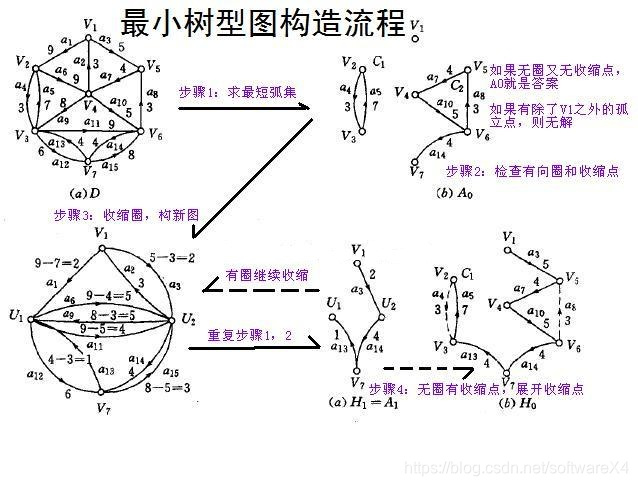
在这里插入图片描述

附上代码：

#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
#define INF 0x7f7f7f7f
const int maxn = 105;
const int maxm = 100050;int n, m;
int in[maxn];  //保存每个点的最小入权值
int pre[maxn];  //保存最小权值的父节点
int vis[maxn], id[maxn]; //vis是访问标识，id是重新分配的节点号
struct E{int from,to,dis;
}edge[maxm];int dist_mst(int n,int m,int root){  //节点数、边数、根节点int ans = 0;while(1){for(int i = 0; i < n;++i)in[i] = INF;for(int i = 0; i < m;++i){int u = edge[i].from;int v = edge[i].to;//非根节点选出最小边，并记录父节点if(in[v] > edge[i].dis && u != v){in[v] = edge[i].dis;pre[v] = u;}}//若除了根节点外还有入度为0的结点，即孤立点，则没有最小生成树for(int i = 0; i < n;++i){if(i == root)continue;if(in[i] == INF)return -1;}memset(vis,-1,sizeof(vis));memset(id,-1,sizeof(id));int cnt = 0;in[root] = 0;for(int i = 0; i < n;++i){ans += in[i];int v = i;//每个不断向上搜寻父节点，要么找到根节点，要么找到自己，形成一个环//id[v] ！= -1意味着当前结点已经被重新分配过节点号了，即已经处理了自环while(vis[v] != i && id[v] == -1 && v != root){vis[v] = i;v = pre[v];}//vis[v] == i 即找到了自环，接下来进行缩点（在一个环内分配同一节点号）if(v != root && id[v] == -1){for(int u = pre[v];u != v;u = pre[u])id[u] = cnt;id[v] = cnt++;}}//没有使用cnt，说明已经没有环，结果已经保存在ans中if(cnt == 0)break;//为不在环中的分配节点号for(int i = 0; i < n;++i){if(id[i] == -1)id[i] = cnt++;}//更新边集节点号for(int i = 0; i < m;++i){int u = edge[i].from;int v = edge[i].to;edge[i].from = id[u];edge[i].to = id[v];if(id[u] != id[v])edge[i].dis -= in[v];//这里id[u] != id[v]说明  edges[i]这条边原来不在有向环中，//如果这条边指向了有向环，那么它的边权就要减少  in[v] 等价于整个环的边权减去in[v]//而如果没有指向有向环，说明它与这个有向环毫无关系，那么在之前的寻找自环缩点过程中已经把这条边的权值加上了，所以这里避免重复计算让这条边的权值减小in[v]变为0}n = cnt;root = id[root];}return ans;}
int main(){int n,m;scanf("%d%d",&n,&m);for(int i=0;i<m;i++){scanf("%d%d%d",&edge[i].from,&edge[i].to,&edge[i].dis);if(edge[i].from==edge[i].to)edge[i].dis=INF;}int res=dist_mst(n,m,0);if(res==-1)printf("No\n");elseprintf("%d\n",res);return 0;
}

一道例题：POJ3164 Command Network
这道题套模板，但是要注意把int改为double。(POJ判题真的很严格orz)
附上AC代码：

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>
#define INF 0x3f3f3f3f
using namespace std;
const int maxn = 10001;
const int maxm = 100050;int n, m;
double in[maxn];
int pre[maxn];
int vis[maxn], id[maxn];
struct E{int from,to;double dis;
}edge[maxm];
struct P{double x,y;double getDis(P p){return sqrt((x-p.x)*(x-p.x) + (y-p.y)*(y-p.y));}
}point[maxn];
double dist_mst(int n,int m,int root){double ans = 0;while(1){for(int i = 0; i< n;++i)in[i] = INF;for(int i = 0; i < m;++i){int u = edge[i].from;int v = edge[i].to;if(in[v] > edge[i].dis && u != v){in[v] = edge[i].dis;pre[v] = u;}}for(int i = 0; i < n;++i){if(i == root)continue;if(in[i] == INF)return -1;}memset(vis,-1,sizeof(vis));memset(id,-1,sizeof(id));int cnt = 0;in[root] = 0;for(int i = 0; i < n;++i){ans += in[i];int v = i;while(vis[v] != i && id[v] == -1 && v != root){vis[v] = i;v = pre[v];}if(v != root && id[v] == -1){for(int u = pre[v];u != v;u = pre[u])id[u] = cnt;id[v] = cnt++;}}if(cnt == 0)break;for(int i = 0; i < n;++i){if(id[i] == -1)id[i] = cnt++;}for(int i = 0; i < m;++i){int u = edge[i].from;int v = edge[i].to;edge[i].from = id[u];edge[i].to = id[v];if(id[u] != id[v])edge[i].dis -= in[v];}n = cnt;root = id[root];}return ans;}
int main(){int n,m;while(~scanf("%d%d",&n,&m)){for(int i=0;i<n;i++){scanf("%lf%lf",&point[i].x,&point[i].y);}for(int i = 0; i < m;++i){int x,y;scanf("%d%d",&x,&y);edge[i].from = x-1;edge[i].to = y-1;if(edge[i].from != edge[i].to) edge[i].dis = point[x-1].getDis(point[y-1]);else edge[i].dis = INF;}double res=dist_mst(n,m,0);if(res==-1)printf("poor snoopy\n");elseprintf("%.2lf\n",res);}return 0;
}