最小生成树问题（C语言）

所谓一个 带权图 的最小生成树，就是原图中边的权值最小的生成树 ，所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。

kruskal

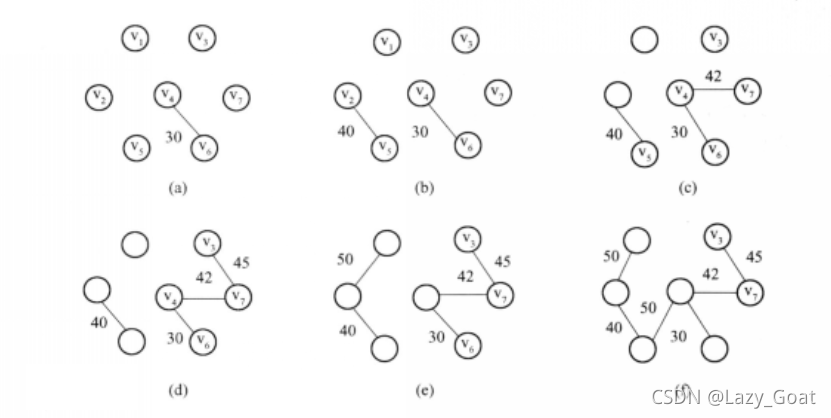
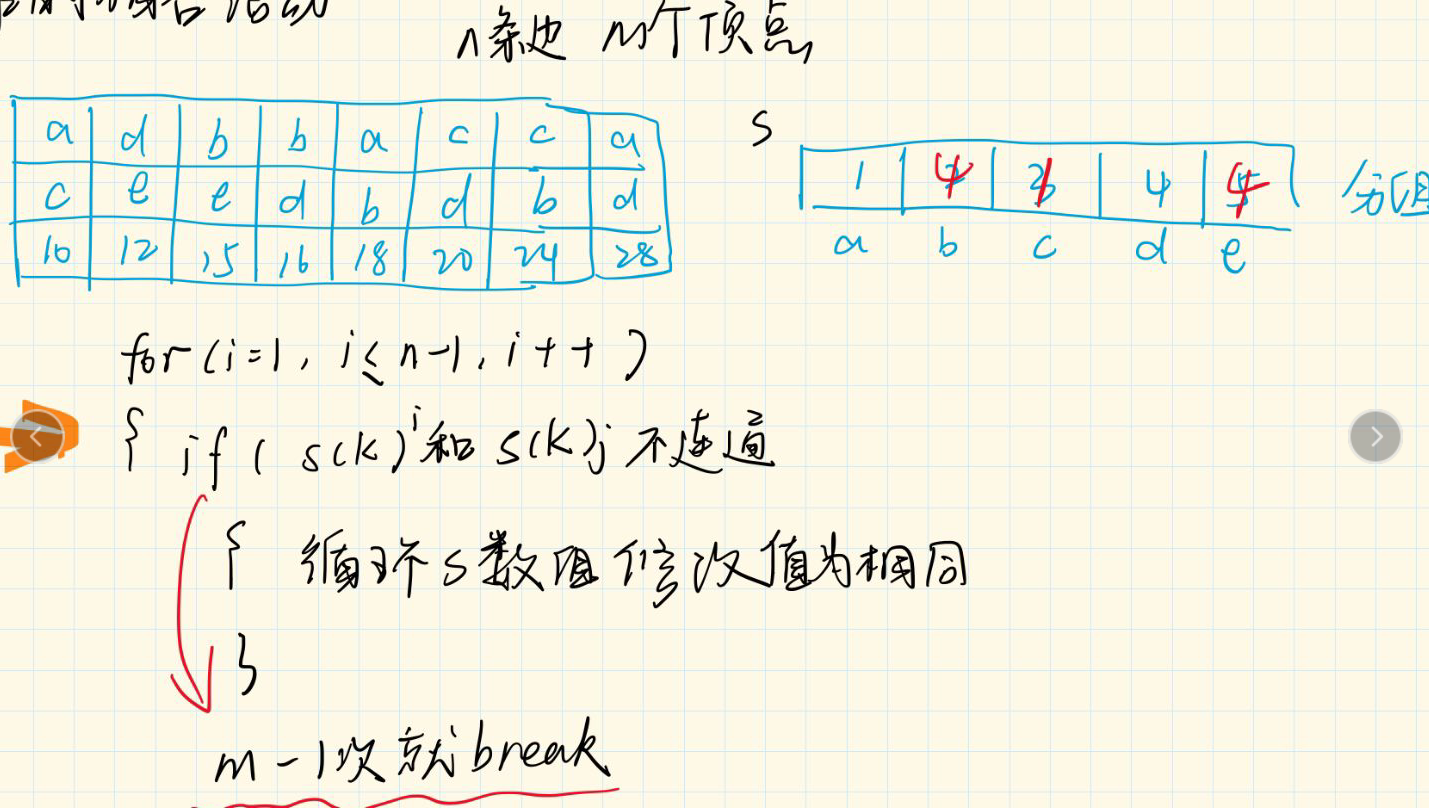
克鲁斯卡尔算法（Kruskal）是一种使用贪婪方法的最小生成树算法。 该算法初始将图视为森林，图中的每一个顶点视为一棵单独的树。 一棵树只与它的邻接顶点中权值最小且不违反最小生成树属性（不构成环）的树之间建立连边。

注意：一定要先排序！！

代码

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
typedef struct
{char letter;int id;
} letter_struct;
typedef struct
{letter_struct one;letter_struct two;int num;
} edge;edge a[MAXSIZE]= {{{'d',4},{'e',5},12},{{'a',1},{'c',3},10},{{'b',2},{'e',5},15},{{'a',1},{'b',2},18},{{'b',2},{'d',4},16},{{'c',3},{'d',4},20},{{'c',3},{'b',2},14},{{'a',1},{'d',4},28}};
int s[MAXSIZE] = {0,1,2,3,4,5};
void kruskal(edge a[MAXSIZE], int row,int column,int jiedian)
{int i,j;int oneid,twoid;int count = 0;for(i=0;i<column;i++){oneid = a[i].one.id;twoid = a[i].two.id;if(s[oneid]!=s[twoid])//说明不连通{for(j=0;j<column;j++){if(s[j]==s[twoid]){s[j]=s[oneid];}}printf("%c---%c:%d\n",a[i].one.letter,a[i].two.letter,a[i].num);count++;if(count>=jiedian-1) break;}}
}
/*排序*/
void simpleseselectsort(edge a[MAXSIZE],int row,int column,int jiedian)
{int i,j,k;edge *tmp = (edge *)malloc(sizeof(edge));for(i=0;i<column;i++){k=i;for(j=i+1;j<column;j++){if(a[j].num < a[k].num) k=j;}if(k!=i){tmp->num = a[i].num;tmp->one = a[i].one;tmp->two = a[i].two;a[i].num = a[k].num;a[i].one = a[k].one;a[i].two = a[k].two;a[k].num = tmp->num;a[k].one = tmp->one;a[k].two = tmp->two;}}
}int main()
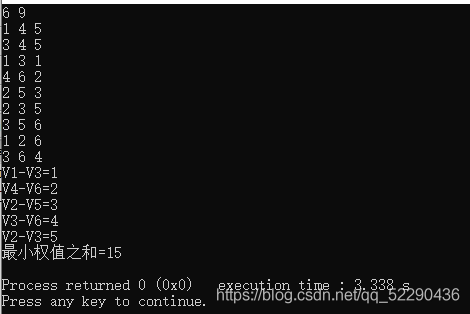
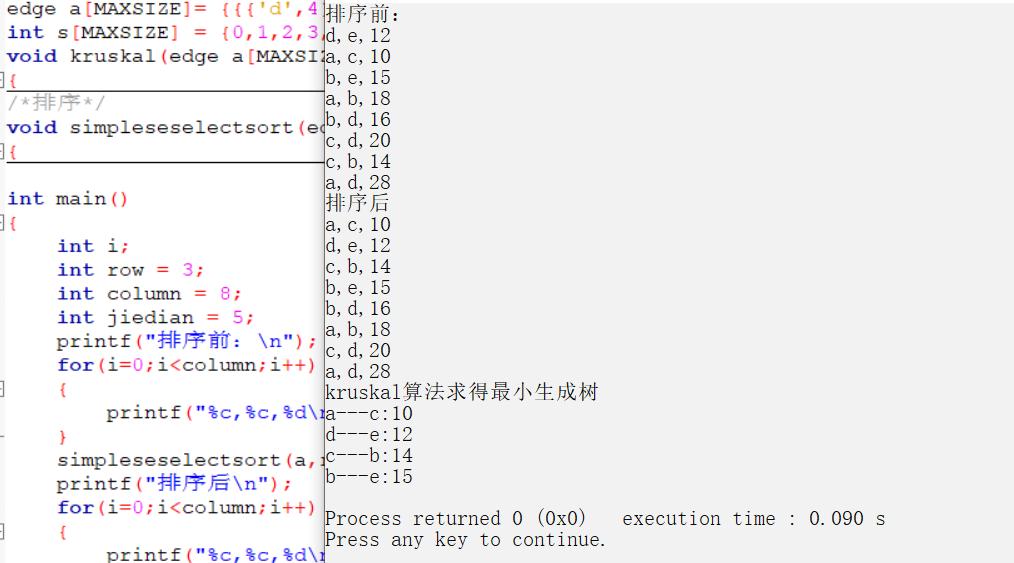
{int i;int row = 3;int column = 8;int jiedian = 5;printf("排序前：\n");for(i=0;i<column;i++){printf("%c,%c,%d\n",a[i].one.letter,a[i].two.letter,a[i].num);}simpleseselectsort(a,row,column,jiedian);printf("排序后\n");for(i=0;i<column;i++){printf("%c,%c,%d\n",a[i].one.letter,a[i].two.letter,a[i].num);}printf("kruskal算法求得最小生成树\n");kruskal(a,row,column,jiedian);
}

截图

prim

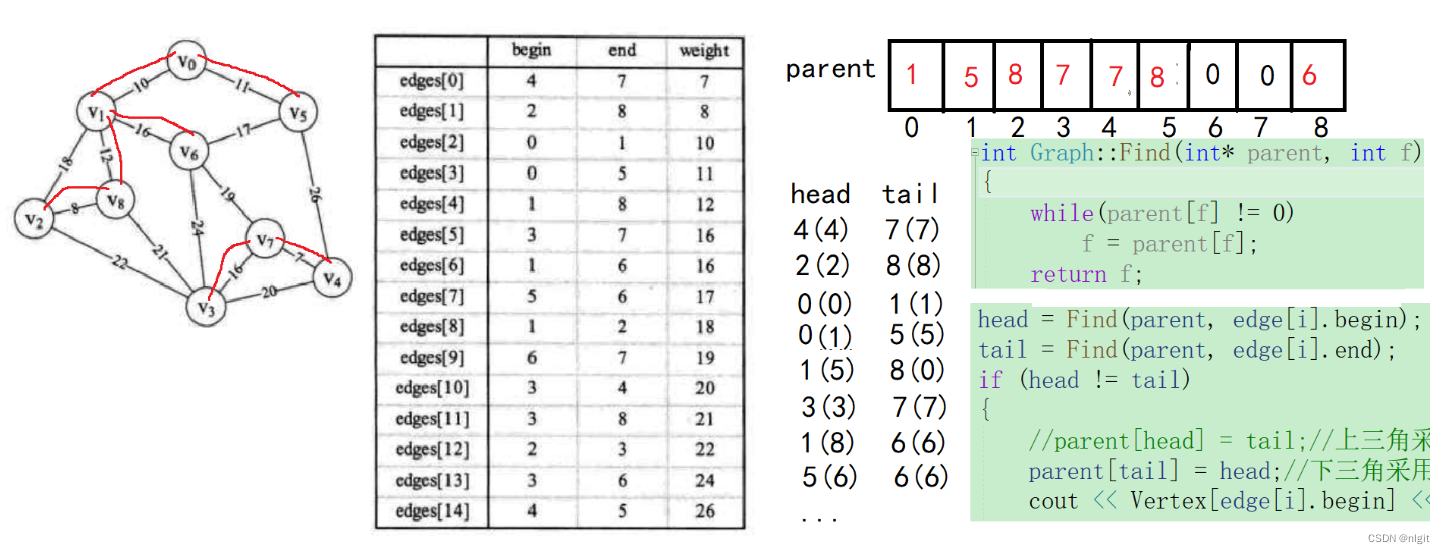
普里姆算法在找最小生成树时，将顶点分为两类，一类是在查找的过程中已经包含在生成树中的顶点（假设为 A 类），剩下的为另一类（假设为 B 类）。

对于给定的连通网，起始状态全部顶点都归为 B 类。在找最小生成树时，选定任意一个顶点作为起始点，并将之从 B 类移至 A 类；然后找出 B 类中到 A 类中的顶点之间权值最小的顶点，将之从 B 类移至 A 类，如此重复，直到 B 类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。

代码main.c

#include <stdio.h>
#include <stdlib.h>
#define FINITY 100
#include "sequence.h"//输入图基本信息
void inputinfo(edgeGraph *G)
{int k;char one,two;int num,oneid,twoid;printf("请输入结点个数:");scanf("%d",&G->jiedian);printf("请输入边数:");scanf("%d",&G->bian);int i,j;//初始化for(i=0;i<G->jiedian;i++){for(j=0;j<G->jiedian;j++){if(i==j) G->edges[i][j]=0;else G->edges[i][j] = FINITY;}}letter_struct shuzu[MAXSIZE] = {{'a',0},{'b',1},{'c',2},{'d',3},{'e',4}};for(i=0;i<G->jiedian;i++){G->vexs[i] = shuzu[i];}printf("请输入边信息：\n");for(k=0;k<G->bian;k++){scanf(" %c %c %d",&one,&two,&num);oneid = getid(one,G);twoid = getid(two,G);G->edges[oneid][twoid] = num;G->edges[twoid][oneid] = num;}return G;
}
//输出矩阵
void outputG(edgeGraph *G)
{int i,j;printf("\n矩阵是：\n");for(i=0;i<G->jiedian;i++){for(j=0;j<G->jiedian;j++){printf("%-5d",G->edges[i][j]);}printf("\n");}printf("\n");
}
//prim
void prim(sequence_queue *sq,int jiedian,int bian,char choose,edgeGraph *G,int count)
{if(count==G->jiedian-1){//read(sq);return ;}//选择的choose字符int chooseid = getid(choose,G);int i,j;char another;edge *tmp = (edge *)malloc(sizeof(edge));printf("你选择的%c的id为%d\n",choose,chooseid);for(j=0;j<jiedian;j++){if(G->edges[chooseid][j]!=FINITY && chooseid!=j){//printf("找到一个edge：id为%d和%d\n",chooseid,j);tmp->one.id = chooseid;tmp->one.letter = choose;tmp->two.id = j;tmp->two.letter = getid_char(j,G);tmp->num = G->edges[chooseid][j];push(sq,tmp);}}//read(sq);another = findmin(sq,count,G);printf("\n接下来找%c\n",another);prim(sq,jiedian,bian,another,G,count+1);
}int main()
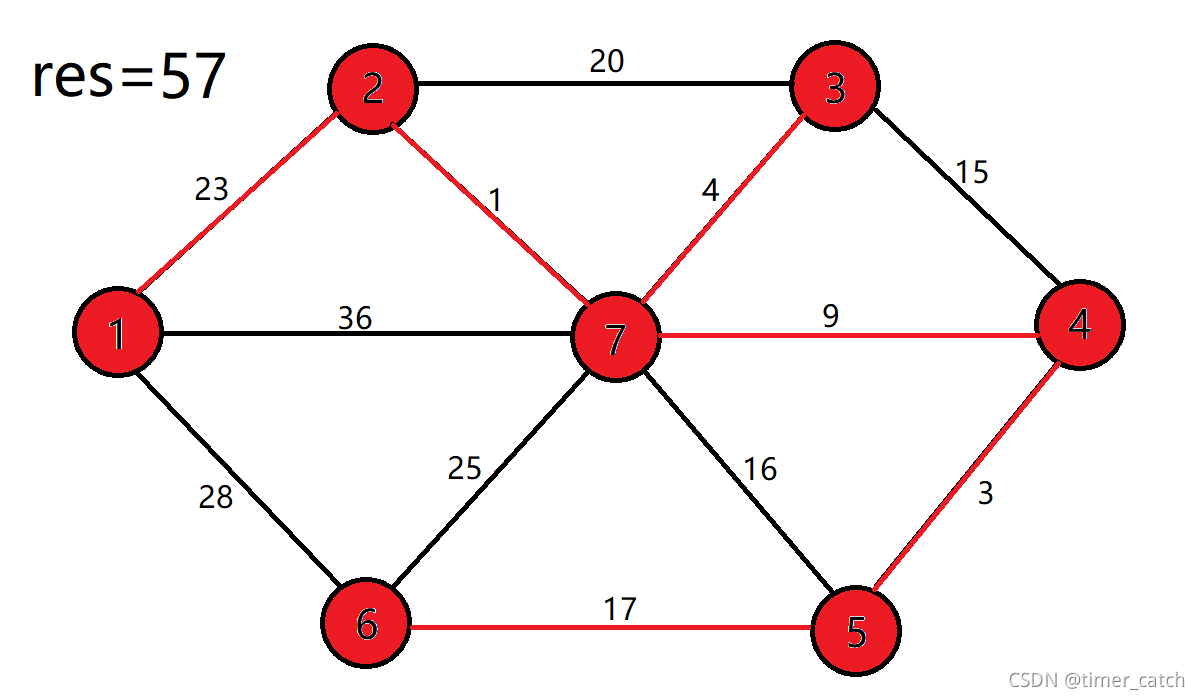
{int i,j,k,num;char one,two;int oneid,twoid;char primchoose;edgeGraph *G = (edgeGraph *)malloc(sizeof(edgeGraph));inputinfo(G);outputG(G);sequence_queue *sq = (sequence_queue *)malloc(sizeof(sequence_queue));init(sq);printf("选择你要第一个开始的结点:");scanf(" %c",&primchoose);prim(sq,G->jiedian,G->bian,primchoose,G,0);
}
/*
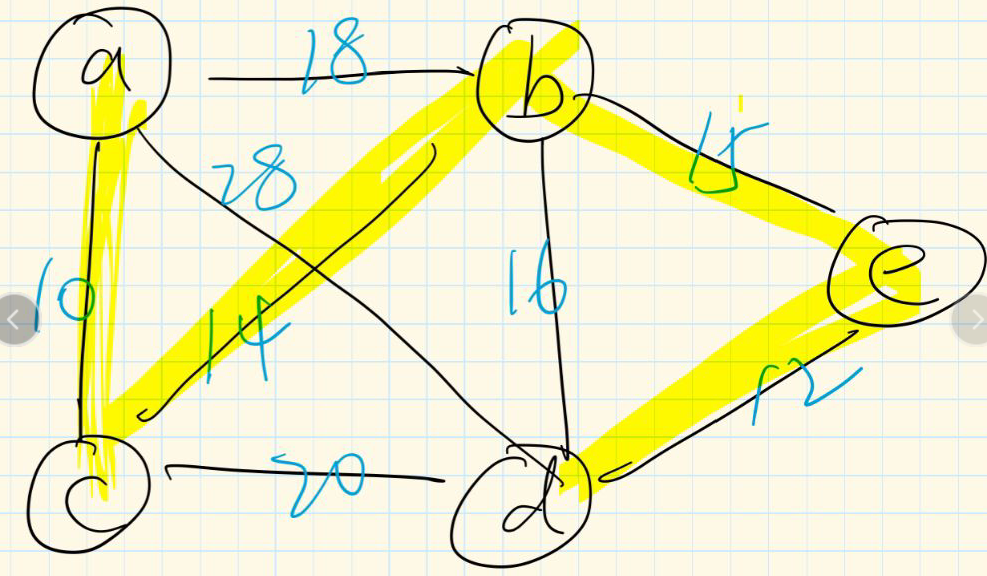
a b 18
a c 10
c d 20
d e 12
b e 15
a d 28
c b 14
b d 16*/

队列sequence.h

#define MAXSIZE 20typedef struct
{char letter;//记录字符int id;//自己字符的id
} letter_struct;typedef struct
{letter_struct one; //记录边第一个顶点的信息letter_struct two;//记录边第二个顶点的信息int num;//记录边的权值
} edge;typedef edge datatype;
//队列
typedef struct{datatype a[MAXSIZE];//队列数组int front;//头指针int rear;//尾指针
}sequence_queue;
//定义图（邻接矩阵
typedef struct
{int jiedian;//结点个数int bian;//边个数letter_struct vexs[MAXSIZE]; //结点信息int edges[MAXSIZE][MAXSIZE];//邻接矩阵
} edgeGraph;//通过字符找id
int getid(char a,edgeGraph *G)
{int k;for(k=0;k<G->jiedian;k++){if(G->vexs[k].letter==a) return G->vexs[k].id;}
}
//通过id找字符
char getid_char(int id,edgeGraph *G)
{int k;for(k=0;k<G->jiedian;k++){if(G->vexs[k].id==id) return G->vexs[k].letter;}
}
//初始化队列
void init(sequence_queue *sq)
{sq->front=sq->rear=0;
}
//队列是否为空
int empty(sequence_queue *sq)
{return (sq->front==sq->rear?0:1);
}
//打印队列
void read(sequence_queue *sq)
{int i;if(!empty(sq)){printf("\n队列是空的！");exit(1);}else{for(i=sq->front;i<sq->rear;i++) printf("%c->%c:%d\n",sq->a[i].one.letter,sq->a[i].two.letter,sq->a[i].num);}
}
//队列pushyige边信息
void push(sequence_queue *sq,edge *x)
{if(sq->rear==MAXSIZE){printf("\n队列满了！");exit(1);}sq->a[sq->rear].num = x->num;sq->a[sq->rear].one = x->one;sq->a[sq->rear].two = x->two;sq->rear=sq->rear+1;
}
//队列中找到count到rear的最小权值边并交换信息到a[count]
char findmin(sequence_queue *sq,int count,edgeGraph *G)
{int i,k;k=count;edge *tmp = (edge *)malloc(sizeof(edge));for(i=count;i<sq->rear;i++){if(sq->a[i].num<sq->a[k].num){k=i;}}printf("最小的一组是：%c--%c:%d\n",sq->a[k].one.letter,sq->a[k].two.letter,sq->a[k].num);if(k!=count){tmp->one = sq->a[count].one;tmp->two = sq->a[count].two;tmp->num = sq->a[count].num;sq->a[count].one = sq->a[k].one;sq->a[count].two = sq->a[k].two;sq->a[count].num = sq->a[k].num;sq->a[k].one = tmp->one;sq->a[k].two = tmp->two;sq->a[k].num = tmp->num;}//read(sq);int oneid,twoid;oneid = getid(sq->a[count].one.letter,G);twoid = getid(sq->a[count].two.letter,G);G->edges[oneid][twoid] = FINITY;G->edges[twoid][oneid] = FINITY;return sq->a[count].two.letter;}void pop(sequence_queue *sq)
{if(sq->rear==sq->front){printf("空队列！");exit(1);}sq->front = sq->front+1;
}

截图

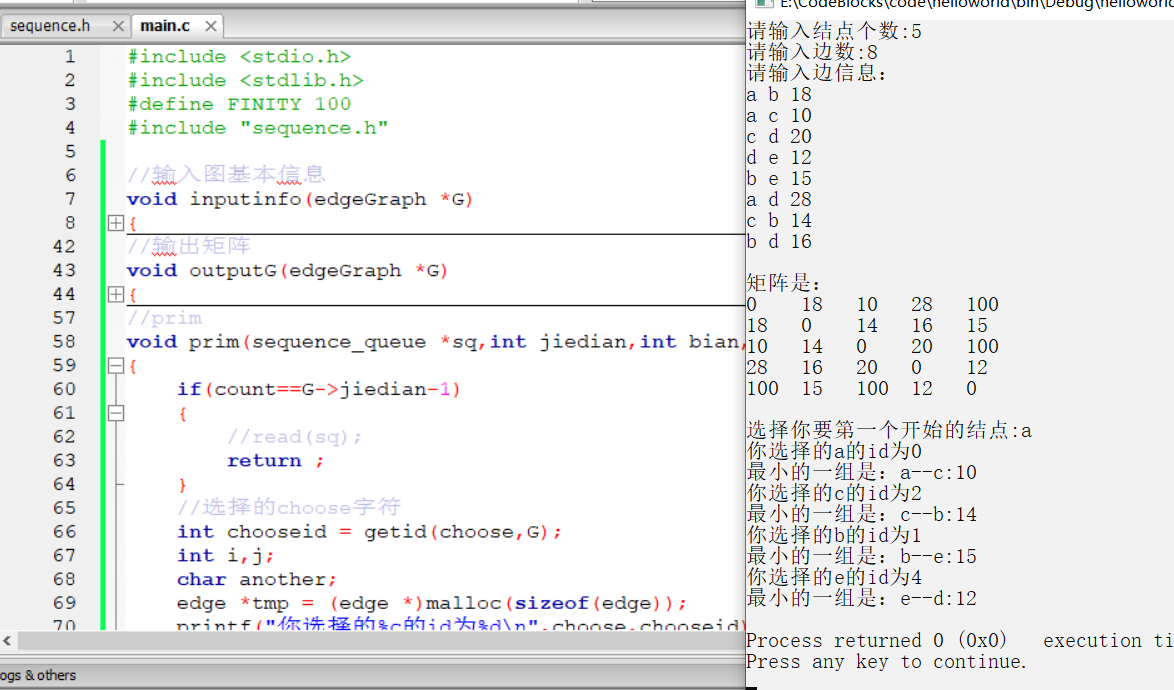
查看队列具体过程