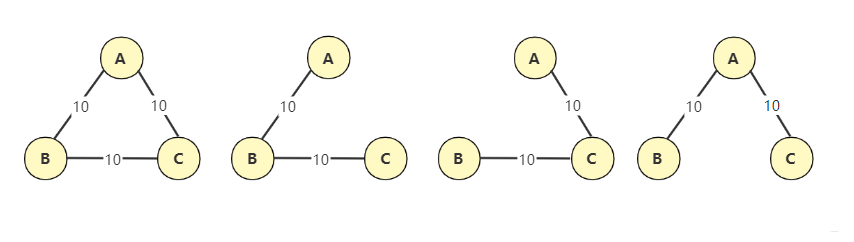
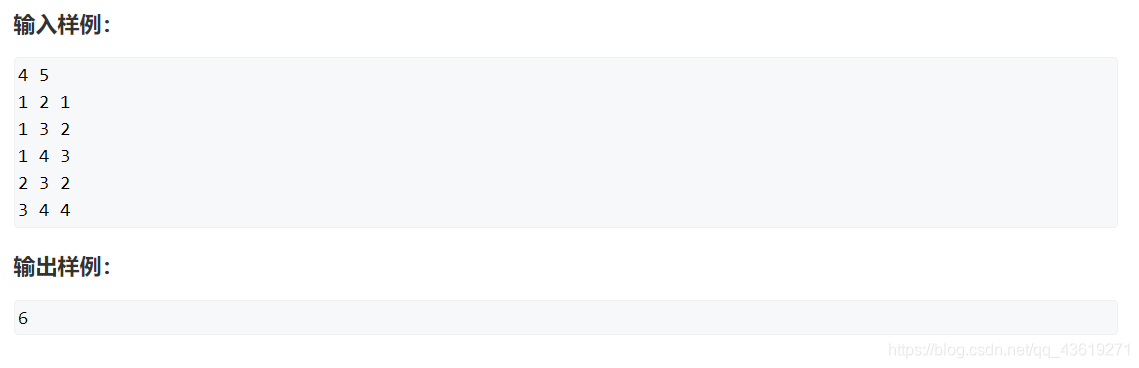
定义:
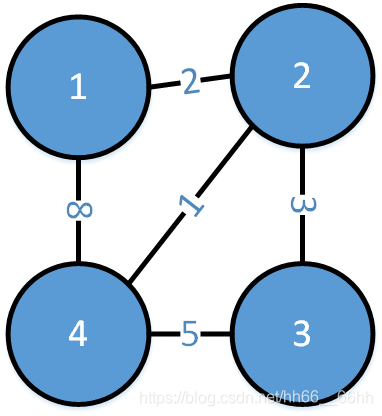
将图中的 n 结点用 n-1 条边连接起来,使其各个边的权值之和最小的生成树。
普里姆算法:
从点的角度出发。
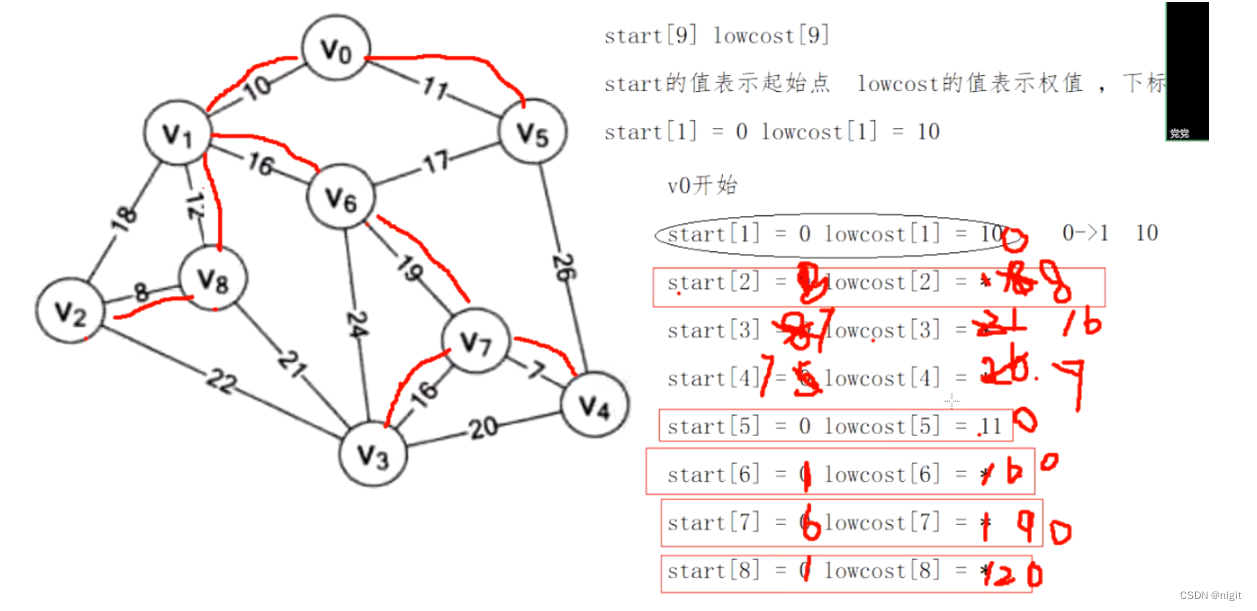
1、start 数组的值表示起始点的下标,start 的下标代表目的顶点;lowcost 数组的下标代表目的顶点,值代表当前结点到目的顶点的权值。
2、每次找出当前结点的最小值后,都需要更新这两个数组。
void Graph::MST_Prim(char vertex)
{int* lowcost = new int[NumVertex];int* start = new int[NumVertex];//start[1] = 0,lowcost[1] = 10,说明从start[1]到1的权值为10,start[1]的值表示起始点的下标,start的下标表示目的顶点int k = GetVertexIndex(vertex);int i, j;//初始化数组for (i = 0; i < NumVertex; i++){if (i == k)lowcost[i] = 0;//从此顶点开始else{lowcost[i] = Edge[k][i];start[i] = k; //初始化从顶点k开始}}//构建MST,生成n-1条边//记录最小值和其下标int min, min_index;int begin, end;for (i = 0; i < NumVertex - 1; i++){//是找出n-1条边,所以注意边界条件min = MAX_WEIGHT;min_index = -1;//查找每次最小的权值for (j = 0; j < NumVertex; j++){if (lowcost[j] != 0 && lowcost[j] < min){min = lowcost[j];min_index = j;}}begin = start[min_index];end = min_index;std::cout << Vertex[begin] << "->" << Vertex[end] << ":" << min << std::endl;lowcost[min_index] = 0;//下次不在访问//更新,min_index是下一轮的起始点的下标for (j = 0; j < NumVertex; j++){int weight = Edge[min_index][j];if (weight < lowcost[j]){//更新权值数组,以及各个顶点的起始顶点lowcost[j] = weight;start[j] = min_index;}}}delete[] start;delete[] lowcost;//防止失效指针start = NULL;lowcost = NULL;
}
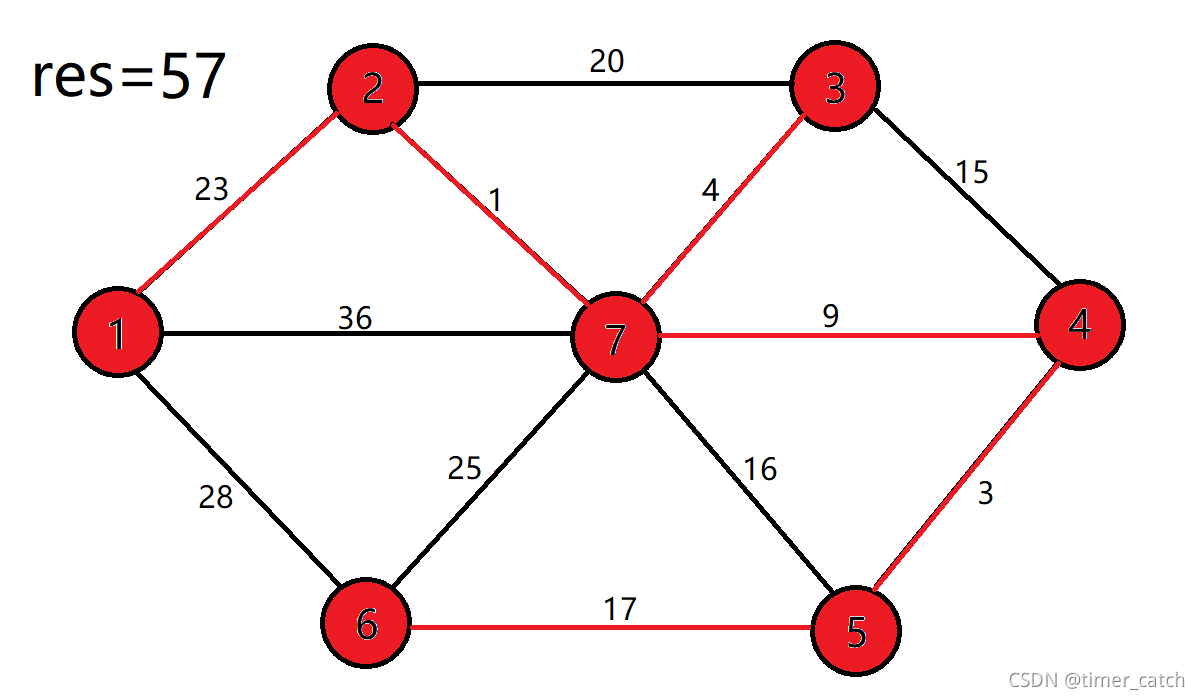
克鲁斯卡尔算法:
从边的角度出发。
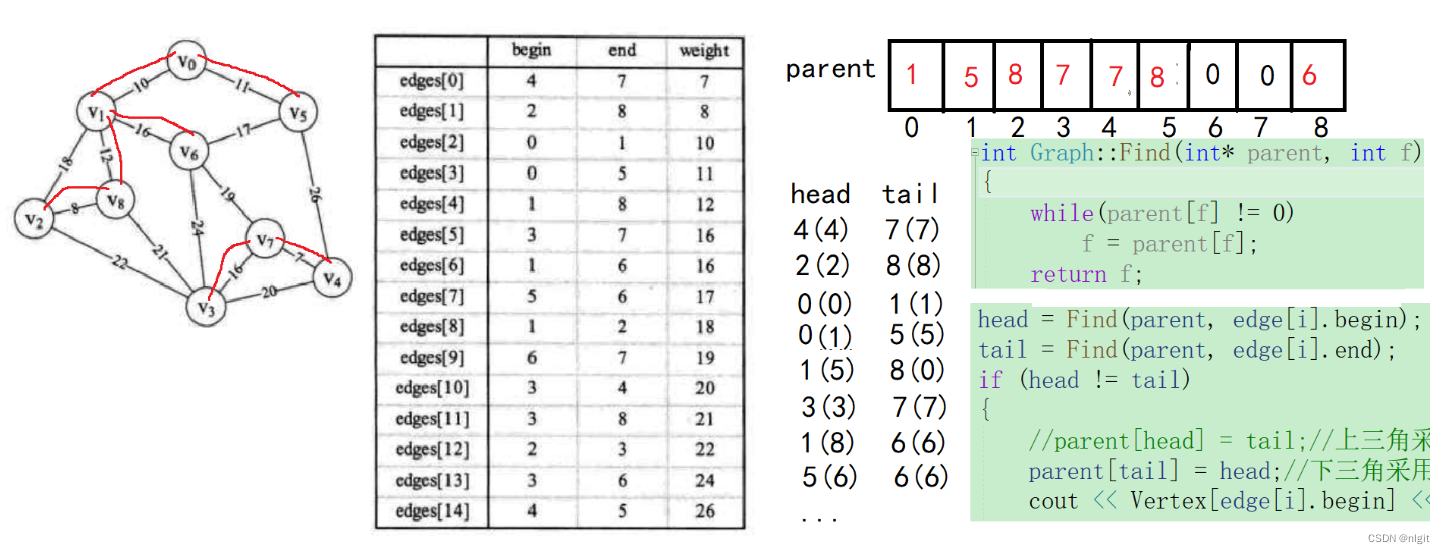
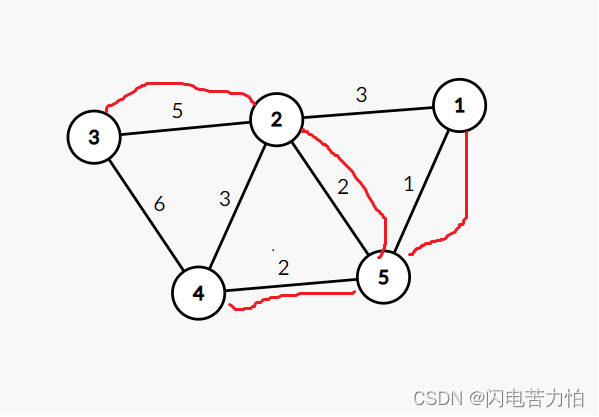
如图,当选择v5--v6这条边后,会构成回路,根据判断条件就不会更新parent 数组,从而不会输出这一选择。
1、先排序,因为要符合MST思想
2、整个算法的关键就是理解Find 函数,虽然只有两行,但是需要画图才能更好理解。
int Graph::Find(int* parent, int f)
{//如果返回值相同,说明选择当前传进来的边会构成回路,这里传边是通过传其两个顶点来判断while(parent[f] != 0)f = parent[f];return f;
}
void Graph::EdgeSort(EDGE* edge)
{int k = 0;for (int i = 0; i < NumVertex; i++){for (int j = 0; j < i; j++){//当前选择下三角if (Edge[i][j] != 0 && Edge[i][j] != MAX_WEIGHT){edge[k].begin = i;edge[k].end = j;edge[k].weight = Edge[i][j];k++;}}}EDGE t;for (int i = 0; i < k; i++){for (int j = 0; j < k - i - 1; j++){if (edge[j].weight > edge[j + 1].weight){t = edge[j];edge[j] = edge[j + 1];edge[j + 1] = t;}}}
}
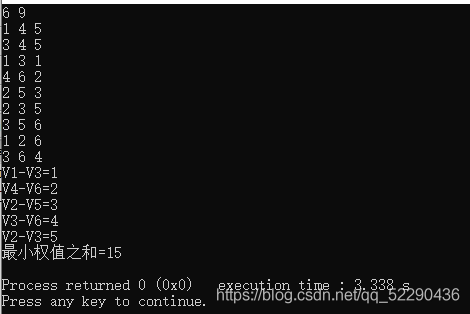
void Graph::Kruskal_MST()
{EDGE* edge = new EDGE[NumEdge];EdgeSort(edge);for (int i = 0; i < NumEdge; i++){cout << edge[i].weight << " ";}static int* parent = new int[NumVertex];int i;int n = 0; //最终选边的条数int head, tail;for (i = 0; i < NumVertex; i++)parent[i] = 0;for (i = 0; i < NumEdge; i++){if (n == NumVertex - 1)break;head = Find(parent, edge[i].begin);tail = Find(parent, edge[i].end);if (head != tail){//parent[head] = tail;//上三角采用的赋值方式parent[tail] = head;//下三角采用的赋值方式cout << Vertex[edge[i].begin] << "->" << Vertex[edge[i].end] << edge[i].weight << endl;n++;}}delete[]edge;edge = NULL;
}