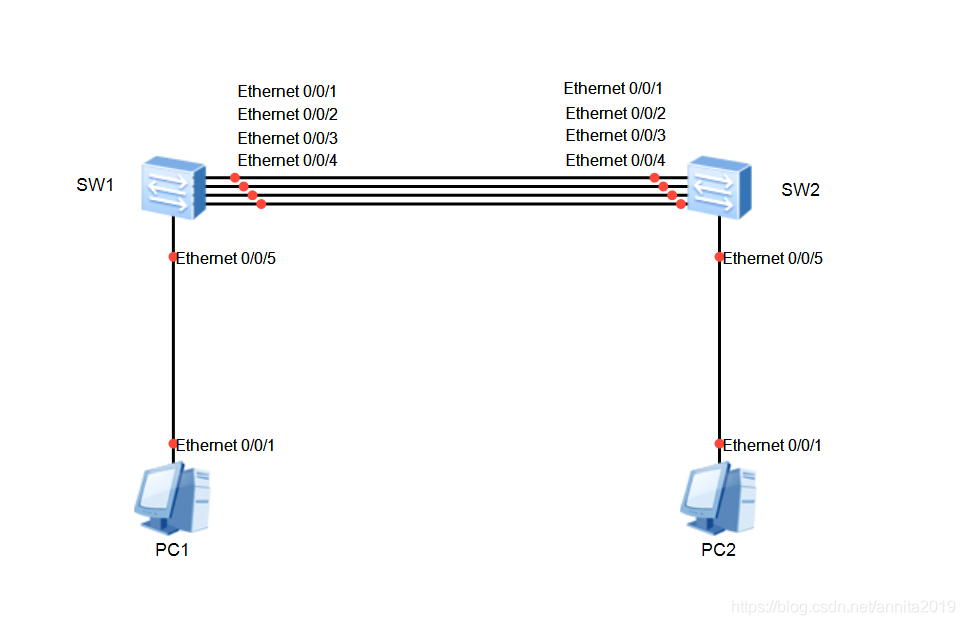
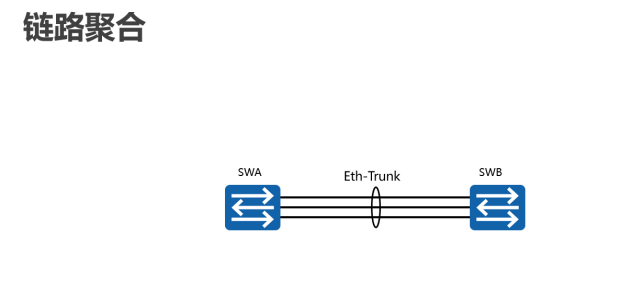
在企业网络中,所有设备的流量在转发到其他网络前都会汇聚到核心层,再由核心区设备转发到其他网络,或者转发到外网。因此,在核心层设备负责数据的高速交换时,容易发生拥塞。在核心层部署链路聚合,可以提升整个网络的数据吞吐量,解决拥塞问题。本示例中,两台核心交换机SWA和SWB之间通过两条成员链路互相连接,通过部署链路聚合,可以确保SWA和SWB之间的链路不会产生拥塞。
-
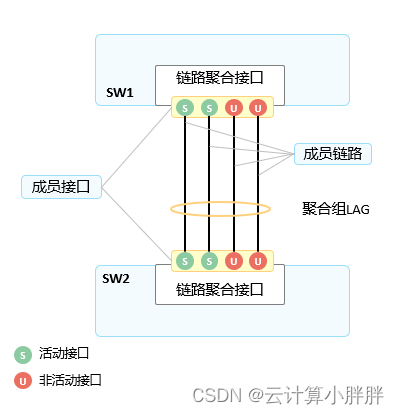
链路聚合是把两台设备之间的多条物理链路聚合在一起,当做一条逻辑链路来使用。这两台设备可以是一对路由器,一对交换机,或者是一台路由器和一台交换机。一条聚合链路可以包含多条成员链路,在ARG3系列路由器和X7系列交换机上默认最多为8条。
-
链路聚合能够提高链路带宽。理论上,通过聚合几条链路,一个聚合口的带宽可以扩展为所有成员口带宽的总和,这样就有效地增加了逻辑链路的带宽。
-
链路聚合为网络提供了高可靠性。配置了链路聚合之后,如果一个成员接口发生故障,该成员口的物理链路会把流量切换到另一条成员链路上。
-
链路聚合还可以在一个聚合口上实现负载均衡,一个聚合口可以把流量分散到多个不同的成员口上,通过成员链路把流量发送到同一个目的地,将网络产生拥塞的可能性降到最低。
-
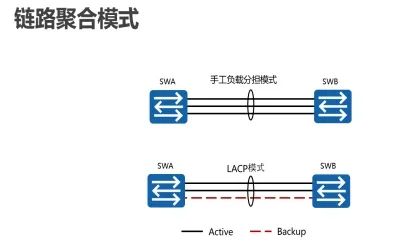
链路聚合包含两种模式:手动负载均衡模式和LACP(Link Aggregation Control Protocol)模式。
-
手工负载分担模式下,Eth-Trunk的建立、成员接口的加入由手工配置,没有链路聚合控制协议的参与。该模式下所有活动链路都参与数据的转发,平均分担流量,因此称为负载分担模式。如果某条活动链路故障,链路聚合组自动在剩余的活动链路中平均分担流量。当需要在两个直连设备间提供一个较大的链路带宽而设备又不支持LACP协议时,可以使用手工负载分担模式。ARG3系列路由器和X7系列交换机可以基于目的MAC地址,源MAC地址,或者基于源MAC地址和目的MAC地址,源IP地址,目的IP地址,或者基于源IP地址和目的IP地址进行负载均衡。
-
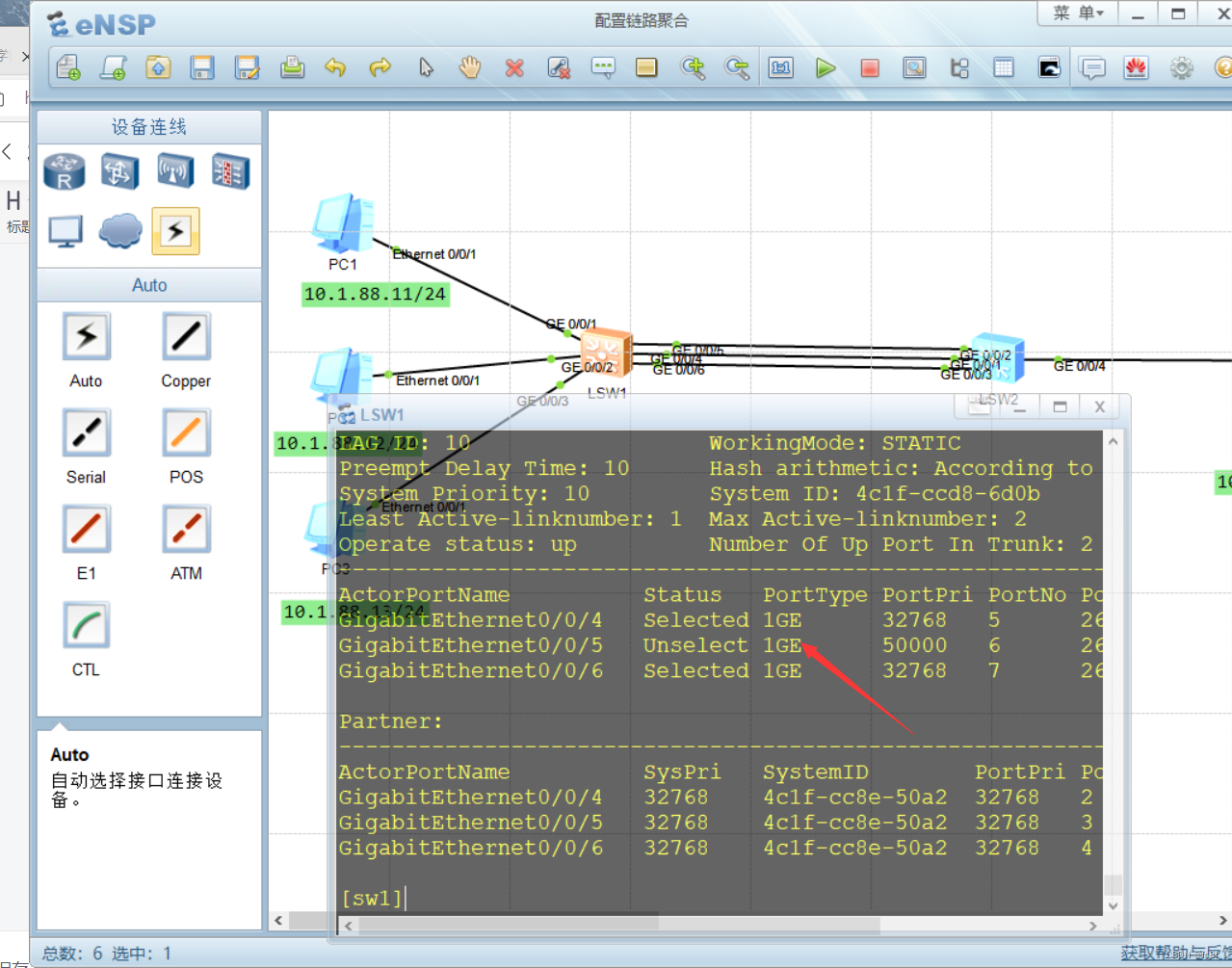
在LACP模式中,链路两端的设备相互发送LACP报文,协商聚合参数。协商完成后,两台设备确定活动接口和非活动接口。在LACP模式中,需要手动创建一个Eth-Trunk口,并添加成员口。LACP协商选举活动接口和非活动接口。LACP模式也叫M:N模式。M代表活动成员链路,用于在负载均衡模式中转发数据。N代表非活动链路,用于冗余备份。如果一条活动链路发生故障,该链路传输的数据被切换到一条优先级最高的备份链路上,这条备份链路转变为活动状态。
-
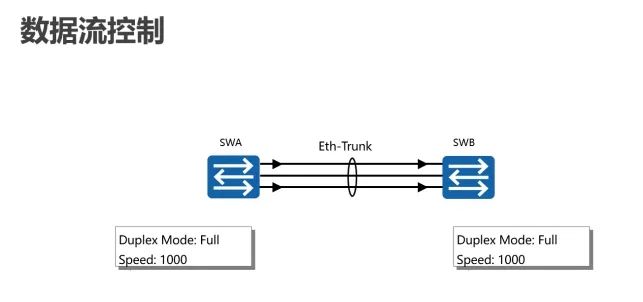
两种链路聚合模式的主要区别是:在LACP模式中,一些链路充当备份链路。在手动负载均衡模式中,所有的成员口都处于转发状态。
-
在一个聚合口中,聚合链路两端的物理口(即成员口)的所有参数必须一致,包括物理口的数量,传输速率,双工模式和流量控制模式。成员口可以是二层接口或三层接口。
-
数据流在聚合链路上传输,数据顺序必须保持不变。一个数据流可以看做是一组MAC地址和IP地址相同的帧。例如,两台设备间的SSH或SFTP连接可以看做一个数据流。如果未配置链路聚合,只是用一条物理链路来传输数据,那么一个数据流中的帧总是能按正确的顺序到达目的地。配置了链路聚合后,多条物理链路被绑定成一条聚合链路,一个数据流中的帧通过不同的物理链路传输。如果第一个帧通过一条物理链路传输,第二个帧通过另外一条物理链路传输,这样一来同一数据流的第二个数据帧就有可能比第一个数据帧先到达对端设备,从而产生接收数据包乱序的情况。
-
为了避免这种情况的发生,Eth-Trunk采用逐流负载分担的机制,这种机制把数据帧中的地址通过HASH算法生成HASH-KEY值,然后根据这个数值在Eth-Trunk转发表中寻找对应的出接口,不同的MAC或IP地址HASH得出的HASH-KEY值不同,从而出接口也就不同,这样既保证了同一数据流的帧在同一条物理链路转发,又实现了流量在聚合组内各物理链路上的负载分担,即逐流的负载分担。逐流负载分担能保证包的顺序,但不能保证带宽利用率。
-
负载分担的类型主要包括以下几种,用户可以根据具体应用选择不同的负载分担类型。
-
根据报文的源MAC地址进行负载分担;
-
根据报文的目的MAC地址进行负载分担;
-
根据报文的源IP地址进行负载分担;
-
根据报文的目的IP地址进行负载分担;
-
根据报文的源MAC地址和目的MAC地址进行负载分担;
-
根据报文的源IP地址和目的IP地址进行负载分担;
根据报文的VLAN、源物理端口等对L2、IPv4、IPv6和MPLS报文进行增强型负载分担。
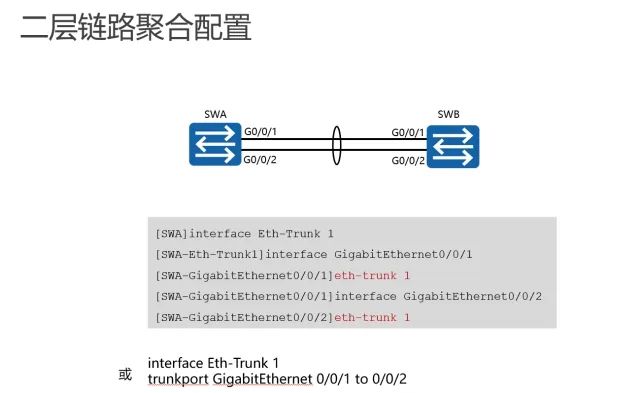
通过执行interface Eth-trunk <trunk-id>命令配置链路聚合。这条命令创建了一个Eth-Trunk口,并且进入该Eth-Trunk口视图。trunk-id用来唯一标识一个Eth-Trunk口,该参数的取值可以是0到63之间的任何一个整数。如果指定的Eth-Trunk口已经存在,执行interface eth-trunk命令会直接进入该Eth-Trunk口视图。

-
如果要在路由器上配置三层链路聚合,需要首先创建Eth-Trunk接口,然后在Eth-Trunk逻辑口上执行undo portswitch命令,把聚合链路从二层转为三层链路。执行undo portswitch命令后,可以为Eth-Trunk逻辑口分配一个IP地址。
[SW1]interface Eth-Trunk 1
[SW1-Eth-Trunk1]mode lacp-static ----默认是munual
[SW1-Eth-Trunk1]trunkport GigabitEthernet 0/0/1 to 0/0/3
[SW1]interface Eth-Trunk 1
[SW1-Eth-Trunk1]max active-linknumber 2----设置两条活动的链路,一条充当备份[SW2]interface Eth-Trunk 1
[SW2-Eth-Trunk1]mode lacp-static
[SW2-Eth-Trunk1]trunkport GigabitEthernet 0/0/1 to 0/0/3
[SW2]interface Eth-Trunk 1
[SW2-Eth-Trunk1]max active-linknumber
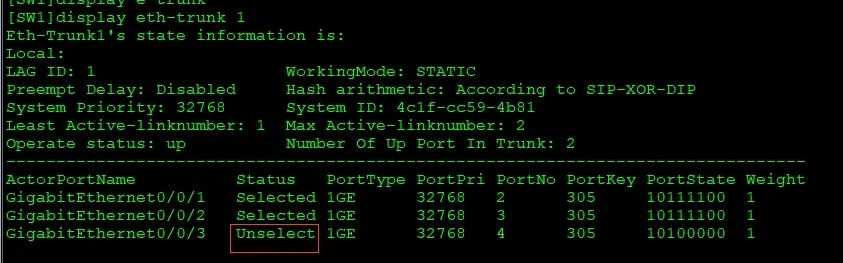
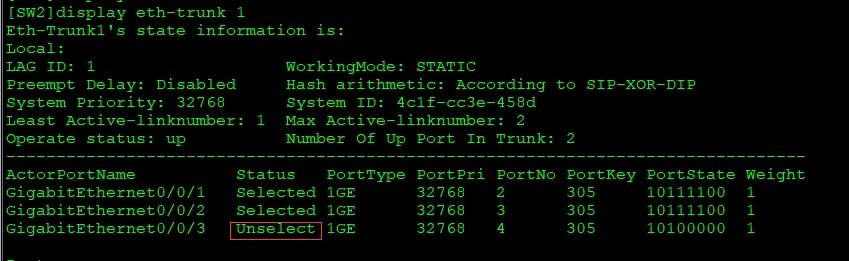
当某条链路出现1或者2链路出现故障3口会启用;当现在链路1或者2链路恢复正常以后你会发现1或2口不会恢复回转发的状态,因为没有开启抢占功能;所以要开启它的抢占功能:
[SW2]interface Eth-Trunk 1
[SW1-Eth-Trunk1]lacp preempt enable
决定链路转发状态:
链路处于转发状态由active交换机说了算,active交换机在根据端口优先级+端口号来判断(越小越优先)
可以修改优先级成为active
[SW1]lacp priority 100
接口优先级修改
int g0/0/3
lacp priority 100
end