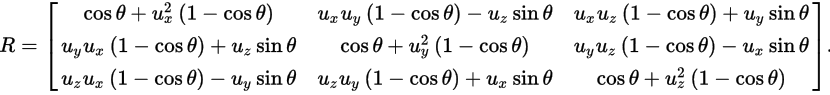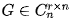----------------------- 摘自 【维基百科】-----------

变换矩阵是数学线性代数中的一个概念。

在线性代数中，线性变换能够用矩阵表示。如果T是一个把Rⁿ映射到R^m的线性变换，且x是一个具有n个元素的列向量，那么

{\displaystyle T({\vec {x}})=\mathbf {A} {\vec {x}}}

我们把m×n的矩阵A，称为T的变换矩阵。

应用[编辑]

任意线性变换都可以用矩阵表示为易于计算的一致形式^[1]，并且多个变换也可以很容易地通过矩阵的相乘连接在一起。

线性变换不是唯一可以用矩阵表示的变换。Rⁿ维的仿射变换与透视投影都可以用齐次坐标表示为RPⁿ⁺¹维（即n+1维的真实投影空间）的线性变换。因此，在三维计算机图形学中大量使用着4x4的矩阵变换。

寻找变换矩阵[编辑]

如果已经有一个函数型的线性变换{\displaystyle T(x)}，那么通过T对标准基每个向量进行简单变换，然后将结果插入矩阵的列中，这样很容易就可以确定变换矩阵A，即

{\displaystyle \mathbf {A} ={\begin{pmatrix}T({\vec {e}}_{1})&T({\vec {e}}_{2})&\cdots &T({\vec {e}}_{n})\end{pmatrix}}}

例如，函数{\displaystyle T(x)=5x}是线性变换，通过上面的过程得到（假设n = 2）

{\displaystyle T({\vec {x}})=5{\vec {x}}={\begin{pmatrix}5&&0\\0&&5\end{pmatrix}}{\vec {x}}}

在二维图形中的应用示例[编辑]

最为常用的几何变换都是线性变换，这包括旋转、缩放、切变、反射以及正投影。在二维空间中，线性变换可以用2×2的变换矩阵表示。

旋转[编辑]

绕原点逆时针旋转θ度角的变换公式是{\displaystyle x'=x\cos \theta -y\sin \theta }与{\displaystyle y'=x\sin \theta +y\cos \theta }，用矩阵表示为：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\ cos\theta \end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

缩放[编辑]

缩放(反矩阵)公式为{\displaystyle x'=s_{x}\cdot x}与{\displaystyle y'=s_{y}\cdot y}，用矩阵表示为：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}s_{x}&0\\0&s_{y}\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

切变[编辑]

切变有两种可能的形式，平行于x轴的切变为{\displaystyle x'=x+ky}与{\displaystyle y'=y}，矩阵表示为：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}1&k\\0&1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

平行于y轴的切变为{\displaystyle x'=x}与{\displaystyle y'=y+kx}，矩阵表示为：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}1&0\\k&1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

反射[编辑]

为了沿经过原点的直线反射向量，假设（u_x, u_y）为直线方向的单位向量。变换矩阵为：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}2u_{x}^{2}-1&2u_{x}u_{y}\\2u_{x}u_{y}&2u_{y}^{2}-1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

不经过原点的直线的反射是仿射变换，而不是线性变换。

若一座标（x, y）沿直线 {\displaystyle y=(tan\theta )x} 进行反射，则其影像（x', y'）可用以下公式求得：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}cos2\theta &sin2\theta \\sin2\theta &-cos2\theta \end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

正投影[编辑]

为了将向量正投影到一条经过原点的直线，假设（u_x, u_y）是直线方向的单位向量，变换矩阵为：

{\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}u_{x}^{2}&u_{x}u_{y}\\u_{x}u_{y}&u_{y}^{2}\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}

同反射一样，正投影到一条不经过原点的直线的变换是仿射变换，而不是线性变换。

平行投影也是线性变换，也可以用矩阵表示。但是透视投影不是线性变换，必须用齐次坐标表示。

组合变换与逆变换[编辑]

用矩阵表示线性变换的一个主要动力就是可以很容易地进行组合变换以及逆变换。

组合可以通过矩阵乘法来完成。如果A与B是两个线性变换，那么对向量x先进行A变换，然后进行B变换的过程为：

{\displaystyle \mathbf {B} (\mathbf {A} {\vec {x}})=(\mathbf {BA} ){\vec {x}}}

换句话说，先A后B变换的组合等同于两个矩阵乘积的变换。需要注意的是先A后B表示为BA而不是AB。

能够通过两个矩阵相乘将两个变换组合在一起这样的能力就使得可以通过逆矩阵进行变换的逆变换。A ^-1表示A的逆变换。

变换矩阵并不都是可逆的，但通常都可以进行直观的解释。在上一节中，几乎所有的变换都是可逆的。只要{\displaystyle s_{x}}与{\displaystyle s_{y}}都不为零，那么缩放变换也是可逆的。另外，正投影永远是不可逆的。

其它类型的变换[编辑]

仿射变换[编辑]

为了表示仿射变换，需要使用齐次坐标，即用三维向量（x, y, 1）表示二维向量，对于高维来说也是如此。按照这种方法，就可以用矩阵乘法表示变换。{\displaystyle x'=x+t_{x}}; {\displaystyle y'=y+t_{y}}变为

{\displaystyle {\begin{pmatrix}x'\\y'\\1\end{pmatrix}}={\begin{pmatrix}1&0&t_{x}\\0&1&t_{y}\\0&0&1\end{pmatrix}}{\begin{pmatrix}x\\y\\1\end{pmatrix}}}

在矩阵中增加一列与一行，除右下角的元素为1外其它部分填充为0，通过这种方法，所有的线性变换都可以转换为仿射变换。例如，上面的旋转矩阵变为

{\displaystyle {\begin{pmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{pmatrix}}}

通过这种方法，使用与前面一样的矩阵乘积可以将各种变换无缝地集成到一起。

当使用仿射变换时，齐次坐标向量w从来不变，这样可以把它当作为1。但是，透视投影中并不是这样。

透视投影[编辑]

三维计算机图形学中另外一种重要的变换是透视投影。与平行投影沿着平行线将物体投影到图像平面上不同，透视投影按照从投影中心这一点发出的直线将物体投影到图像平面。这就意味着距离投影中心越远投影越小，距离越近投影越大。

最简单的透视投影将投影中心作为坐标原点，z = 1作为图像平面，这样投影变换为{\displaystyle x'=x/z}; {\displaystyle y'=y/z}，用齐次坐标表示为：

{\displaystyle {\begin{pmatrix}x_{c}\\y_{c}\\z_{c}\\w_{c}\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&1&0\end{pmatrix}}{\begin{pmatrix}x\\y\\z\\1\end{pmatrix}}}

(这个乘法的计算结果是{\displaystyle (x_{c},y_{c},z_{c},w_{c})} = {\displaystyle (x,y,z,z)}。）

在进行乘法计算之后，通常齐次元素w_c并不为1，所以为了映射回真实平面需要进行齐次除法，即每个元素都除以w_c：

{\displaystyle {\begin{pmatrix}x'\\y'\\z'\end{pmatrix}}={\begin{pmatrix}x_{c}/w_{c}\\y_{c}/w_{c}\\z_{c}/w_{c}\end{pmatrix}}}

更加复杂的透视投影可以是与旋转、缩放、平移、切变等组合在一起对图像进行变换。