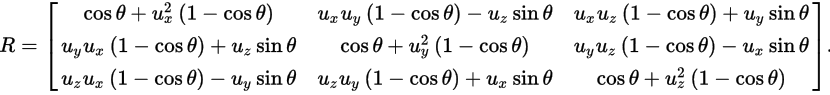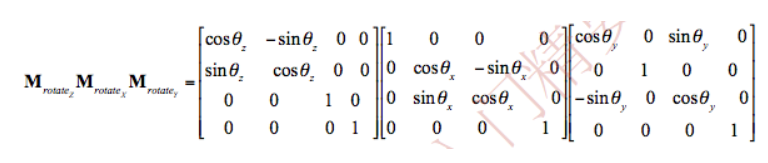文章同时发布于: 王鹏飞的个人网站。
3D图形学中的矩阵变换
从这个月开始,我打算系统的去学习计算机图形学的知识了,一方面是因为兴趣,另一方面是之前自己也写过一些二维图形相关的程序,有一些数学的基础。图形学在软件开发中的地位很高,市面上所有的建模软件都与图形学相关,即使是photoshop这种设计软件也会涉及图形学的知识。而现在由于webgl的发展,未来图形软件在浏览器的比重也会越来越大。
废话不多说了,直接进入正题。本篇文章主要是为了证明图形学中的几种变换矩阵。首先要知道到学习图形学肯定要与向量、矩阵打交道。如果对线性代数不熟,可以先系统的学习下线性代数,要看懂本篇文章,至少你要有矩阵和向量的基础,会矩阵的数乘和乘法。
一. 点和向量
这部分我先简单的介绍下点和向量等基础概念。
平面中任意一个点可以用一个二元数列表示,在笛卡尔坐标系中(0, 0)点表示原点,(1, 1)表示原点往x轴方向移动1步,往y轴方向移动1步得到的点,而向量就形象的表示了这一过程,(0, 0)至(1, 1)点的向量就是(1 - 0, 1 - 0),即(1, 1)。向量是一个表示方向和大小的概念,在物理中可以用来表示力和速度。在三维中,点和向量用三元数列表示(x, y, z),任意一组xyz值可以唯一确定一个点和一个向量。
二. 变换矩阵
在图形学中,在做平移,旋转和缩放时,经常会用到矩阵,有缩放矩阵、平移矩阵和旋转矩阵。在三维空间中,变换矩阵都是一个四维矩阵,每一行分别表示x, y, z, w。为什么是四维的而不是三维的呢?请继续往下阅读。
1. 缩放矩阵(scale)
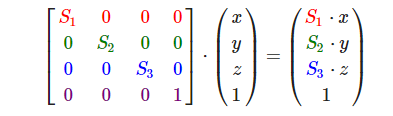
上面的公式,左边的第一个操作数(四维矩阵)就是一个缩放矩阵,s1表示x轴的缩放倍数,s2表示y轴的缩放倍数,s3表示z轴的缩放倍数。第二个操作数表示空间中(x, y, z)点, w分量在缩放矩阵中没有用到,我们将其设为1。由右边的结果,可以看出(x, y, z)点经过缩放矩阵变换后,x、y、z分量都各自缩放了s(s1、s2、s3)倍。需要注意的是矩阵的乘法不具有交换律,这里点是用一维列矩阵表示的,作为矩阵乘法的右操作数。如果将其转换到乘法的左边,那么点应该用一维行矩阵表示:
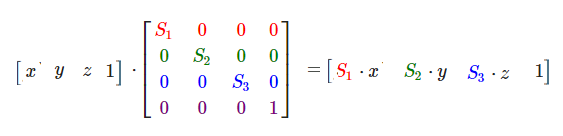
缩放矩阵比较简单,不需要证明,只需要会简单的乘法,就可以看出x,y,z经过缩放矩阵的变换确实被缩放了。
2.平移矩阵(translation)
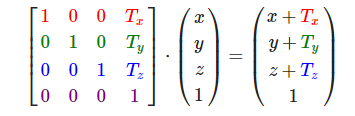
平移矩阵也称位移矩阵,平移矩阵用到了第四列(w列),这也是为什么三维空间变换矩阵为什么是四维的。平移矩阵也比较容易理解,因为可以通过结果看出想x 、y、z确实各自平移了T步。
3. 旋转矩阵
旋转矩阵,相对难一些,也不是那么容易理解,我们先看最基础的绕x、y、z轴旋转的旋转矩阵。
沿x轴:
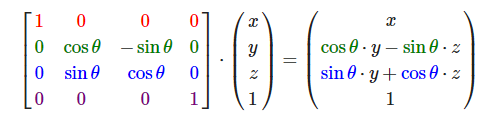
沿y轴:
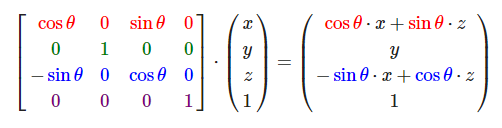
沿z轴:
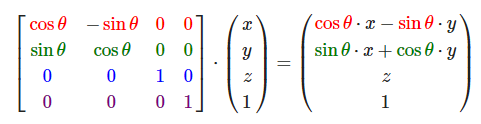
引入了三角函数,我们无法从结果看出旋转矩阵是否正确,所以我们需要证明。下面我给出沿z轴旋转的变换矩阵证明过程,其他轴同理可证。
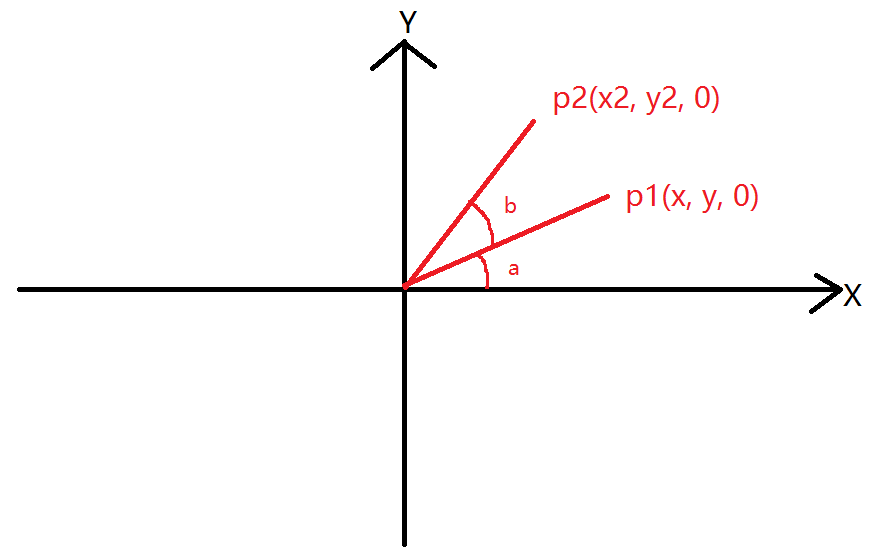
假设有如图的点p1,因为绕z轴旋转,点的z值是不变的,我们将其设为0,这样可以将其模拟成二维平面xy中旋转。假设p1绕原点旋转b角度,初始角度为a。整个证明过程如下:
// 经过旋转后向量的长度不变为L(原点到p1和p2的距离相同)
// 由三角函数得到sin(a + b), cos(a + b)的值
cos(a + b) = x2 / L;
sin(a + b) = y2 / L;// 展开sin(a + b)和cos(a + b)
cos(a) * cos(b) - sin(a) * sin(b) = x2 / L;
sin(a) * cos(b) + cos(a) * sin(b) = y2 / L;// 用x和y表示cos(a)和sin(a)
x / L * cos(b) - y / L * sin(b) = x2 / L;
y / L * cos(b) + x / L * sin(b) = y2 / L;// 等式两边同时乘以L
x * cos(b) - y * sin(b) = x2;
y * cos(b) + x * sin(b) = y2;
将x2和y2的结果与上面z轴旋转矩阵结果比较,发现是完全一样的。
按照上面的方法同理可证绕x轴旋转和绕z轴旋转的矩阵。
那么绕任意轴旋转的矩阵呢?learnOpengl_cn官网直接给出了绕任意轴旋转的矩阵,(Rx, Ry, Rz)表示任意轴,θ表示旋转的矩阵。这个矩阵证明比较复杂。
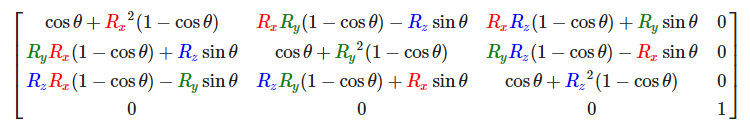
我就不去给大家证明了,我给出证明的思路,大家可以自己尝试去证明。
first,我们可以将绕任意轴旋转转换成绕x,y,z轴旋转。所以先将轴(Rx, Ry, Rz)转换成某一个轴,例如转换成z轴。如图将轴绕Y轴旋转θ角度至yz平面。
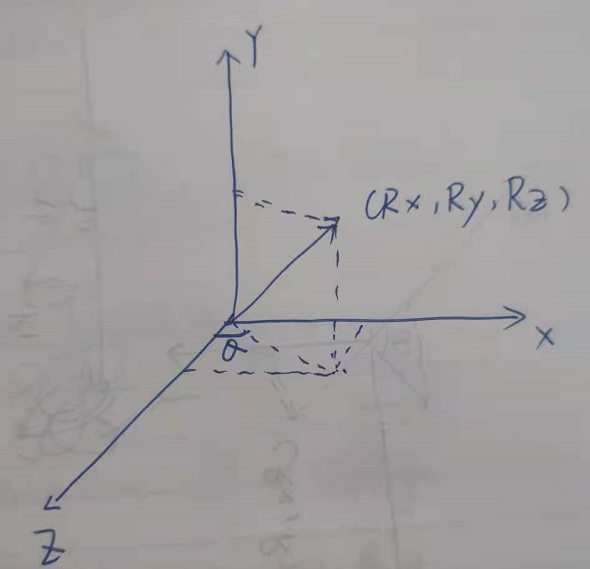
在将轴绕x轴旋转a角度至z轴重合。
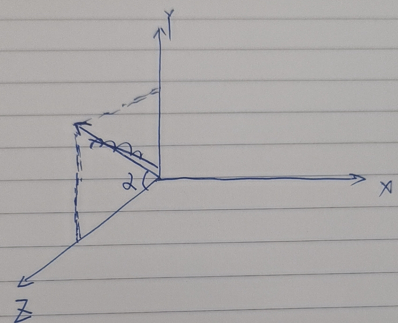
现在物体绕该轴旋转,就是绕z轴旋转了。旋转完成后,我们还需要将旋转轴恢复至最初的位置,即将上面的步骤逆操作一遍,先绕x轴旋转-a角度,再按照y轴旋转-θ角度。这一系列变换最后得到的矩阵就是绕任意轴旋转的矩阵。
继续阅读: 3D图形学中的矩阵变换及证明(二)、3D图形学中的矩阵变换(三)。
(完)。