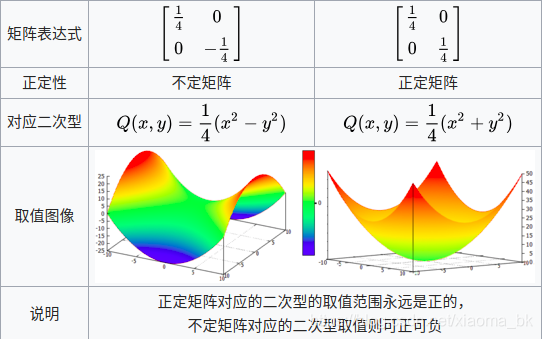
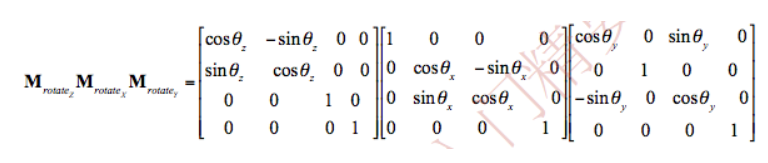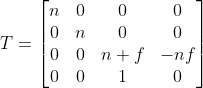计算机图形学之矩阵变换的深度理解

article/2025/9/15 0:38:37

对于图形学来说，矩阵计算不可避免，既直观又方便。而如果线性代数学的不透彻的话，那么基本上是做不到应用的，这里推荐看一下3Blue1Brown的线性代数的视频，可以对矩阵计算有深刻的认识。

之后就是应用阶段，我们这个阶段就是使用我们的矩阵来完成空间中点或向量的各种变换。

重点是理解矩阵的含义：矩阵其实是一种坐标系的转换

理解矩阵的几何功能:
1. 矩阵是一种线性变换（线段变换后仍是线段，并且原点不会改变）
2. 矩阵是一种映射，映射可以是一对一，也可以是一对多
3. 矩阵是一种空间变换，每一种矩阵都是有本身的几何意义，而不是单纯的数字组合
理解矩阵的形式含义（矩阵在左，向量在右）：
1. 方阵满秩，是进行当前空间的坐标变换，不会进行维度的升高和降低
2. M×N(M>N),这种矩阵是一种升维矩阵，几何意义如3×2，就如同把一个平面进行一个方向维度的延展（当秩为2时），变成一个三维的空间，当然之前空间中的点（x,y）在提升维度的过程中在三维空间中还是一个平面分布，只是多了一个值全相等的第三个维度的值而已
3. M×N(M<N),这是一种降维矩阵，几何意义如2×3（当秩为2时），是把三维的向量进行一个维度的压缩，挤压成一个平面，这个时候当然会出现很多个点压缩到一个二维坐标的情况
4. 方阵不满秩，其实和之前是一样的，不满秩就说明这个维度是虚的，没什么用，如果秩是一的话就是挤压成一条线。

一.平移矩阵

当我们理解了之前的种种逻辑之后，我们终于进入到了我们的就事论事环节，首先就是我们的平移矩阵。

我们当然有理由先讨论二维的情况。

1.1二维平移矩阵

形式：平移矩阵的形式是什么样的呢。

一定是一个满秩的矩阵，因为我们并不会进行维度的变换。
坐标轴的方向和长度是不变的，因为矩阵运算的本质是改变的参考系的X，Y。

寻找矩阵：

那么什么样的矩阵能够使得一个点进行平移操作呢，因为平移操作并不会改变参考系XY的方向和单位向量的长度，所以实际上，在当前的维度中，我们并不可能做到，为什么呢？因为我们之前说过，矩阵的线性变换并不会改变原点的位置，矩阵是默认原点就是（0，0），在矩阵中填充任何的值都没办法改变这个约定熟成的决定。那么怎么做到呢，我们利用更高一维的矩阵，也就是三维矩阵进行操作，其实就是在更高的维度当中，解决我们的原点平移问题。

在这里，需要说明的是，如果我们使用的是左矩阵右向量的形式，那么构成我们全新的坐标系的向量应当是矩阵中的列。我们在增加了一个新的维度，（dx,dy,1）,dx,dy就是我们要平移的数量，而增加一个1，是因为要保持秩是3，毕竟我们是从更高一层的维度来转移我们的坐标原点的。

从几何意义来说，平移矩阵其实就是增加一个并不正交的Z轴（dx,dy,1）来进行一个坐标轴的重新定义，继而将坐标转换位置。

这里需要注意的是，点V=（x,y,1），并不是再是我们二维坐标上的点，而是以P的列向量为基所构成的三维空间上的点，只是说我们把二维的点变为V=（x,y,1）然后经过对应矩阵P的线性变换，最终得到平移点的位置。

这个过程可能有些难以理解，但是又是那么的巧妙和精确。我们所构造的矩阵P，是通过新空间中基的列向量来构成的，其中的列向量中每一个坐标值对应的数值，其实都是以我们原有的基x=(1,0),y=(0,1)来决定的。P这个矩阵，是一种线性的变换，是把用它坐标系中表示的点的位置坐标，来映射到原先我们确定它的时用的基的空间里。

这其实就是一种投影运算，对V的每个坐标值进行投影。

而p的逆矩阵，其实就是把我们的坐标映射到P的坐标中的运算。