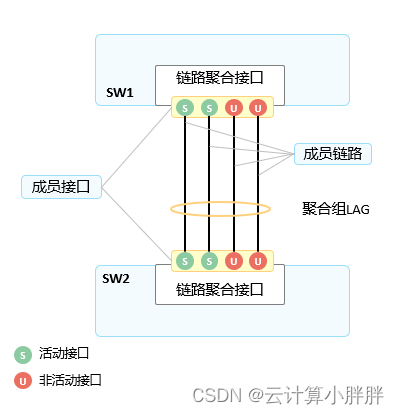
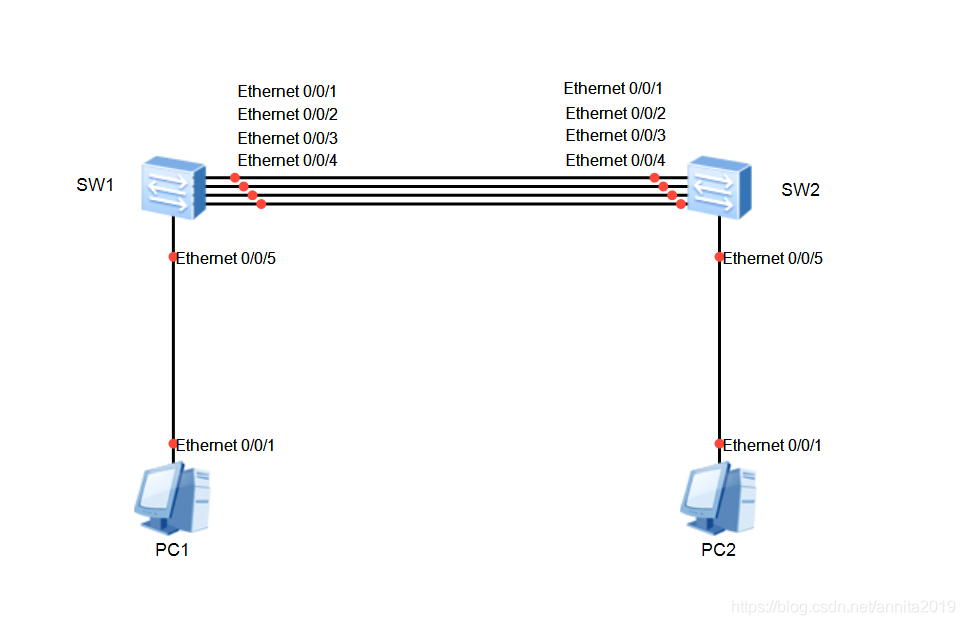
什么是链路聚合
链路聚合(Link Aggregation)亦称主干技术(Trunking)或捆绑技术(Bonding),是将—组物理接口捆绑在一起作为一个逻辑接口来增加带宽的一种方法。随着网络规模不断扩大,用户对骨干链路的带宽及可靠性要求越来越高。在传统技术中,常更换高速率接口板卡或高速率设备来增加带宽,但这种方案成本高,且不够灵活。采用链路聚合技术可以在不进行硬件升级的条件下,将多个物理接口捆绑为一个逻辑接口,实现增加链路带宽的目的。链路聚合技术不仅有效的提高链路可靠性和增加链路带宽,还实现流量在不同物理链路上的负载分担。
链路
链路聚合的优势
提高链路的带宽:理论上,通过链路聚合,可使一个聚合端口的带宽最大为所有成员端口的带宽总和。
提高网络的可靠性:配置了链路聚合的端口,若其中一个端口出现故障,则该成员端口的流量就会切换到其他成员链路中去。保障了网络传输的可靠性。
实现流量的负载均衡:把流量平均分到所有成员链路中。最大限度降低链路中每个成员产生流量阻塞链路的风险。
链路
链路聚合的工作模式
链路聚合总共有两种模式:手动负载均衡模式与LACP(链路聚合控制协议)模式。

手工负载均衡模式
手工负载均衡模式由用户手工配置,不允许系统自动添加或删除汇聚组中的端口。该模式下的所有活动链路都参与数据的转发,平均分担流量。如果某条活动链路出现故障,则自动在剩余的活动链路中平均分担流量。适用于两直连设备之间,既需要大量的带宽,也不支持LACP协议时。可以基于MAC地址和IP地址进行负载均衡,迈普设备共有七种负载均衡模式。
LACP(链路聚合控制协议)模式
静态LACP模式链路聚合是一种利用LACP协议进行参数协商选取活动链路的聚合模式。静态LACP模式下,汇聚组的创建、成员接口的加入,都是由手工配置完成的。但与手工负载分担模式链路聚合不同的是,当新增一组成员接口加入汇聚组时,端口的LACP协议自动使能,通过LACP协议报文协商选择出活动接口与非活动接口,该模式下LACP协议报文参与活动接口的选择。
LACP
LACP协议工作原理
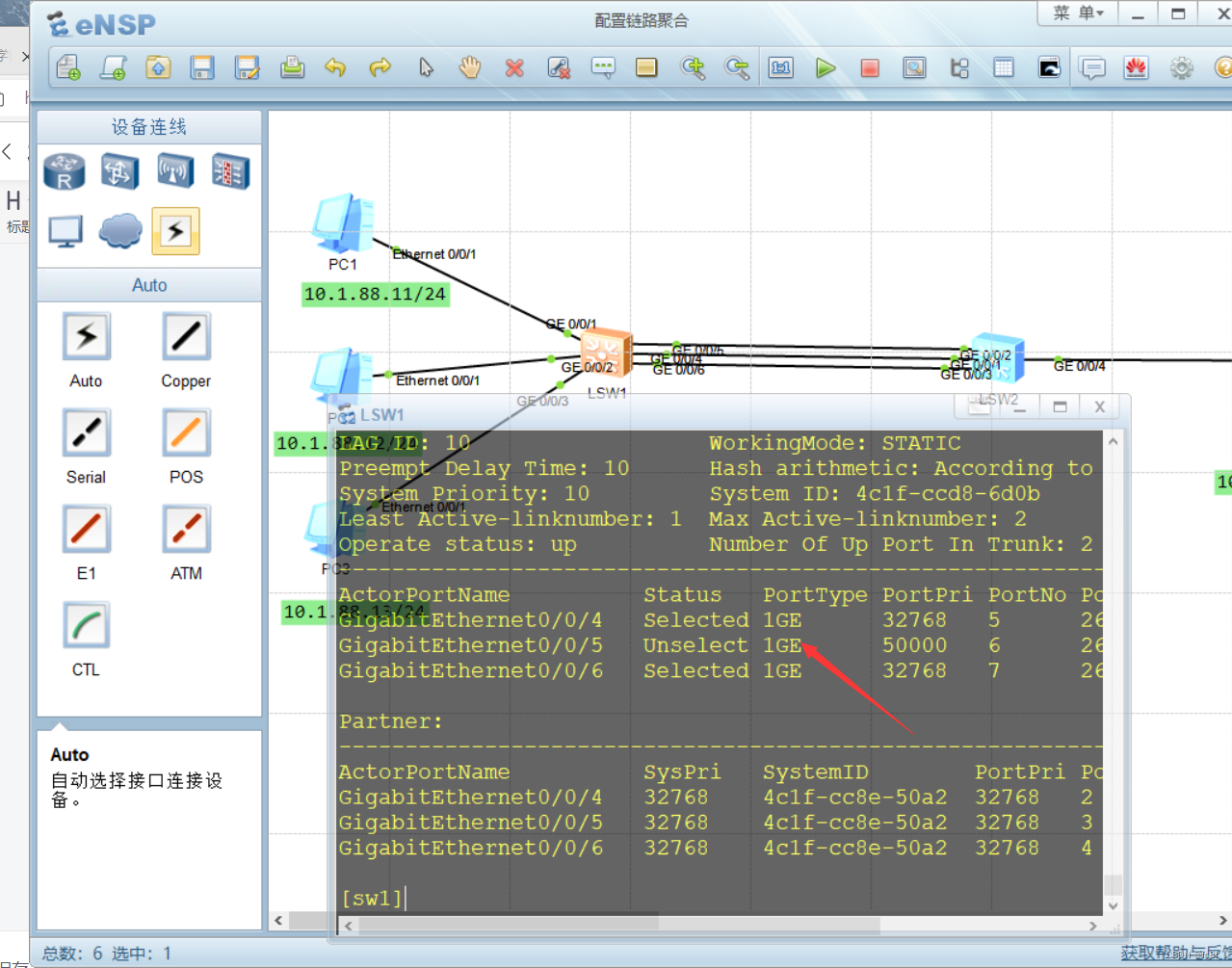
采用LACP聚合的双方(分别称为Actor和Partner)通过称之为LACPDU(LACP Data Unit)的协议报文来交互本端(Actor)和对端(Partner)的聚合信息,以对整个链路聚合的认识达成一致。协议报文主要包含以下信息:系统LACP优先级、系统ID、操作key、端口LACP优先级、端口ID、端口状态。聚合的双方就根据这些信息,按照一定的选择算法选择合适的链路,控制聚合的状态。被选中的成员链路可以正常转发流量,而未被选中的成员链路将被置为阻塞状态,不能转发任何流量。
汇聚端口建立过程如下:
两端互相发送 LACPDU 报文
两端设备根据系统 LACP 优先级确定主动端
两端设备根据端口LACP 优先级确定活动接口,最终以主动端设备的活动端口确定两端的活动端口
LACP聚合后,聚合链路的总带宽等于被选中的成员链路的带宽之和,并且聚合链路上的流量会按照一定的规则分担到各个选中的成员链路上,由于LACPDU是周期性交互,即聚合的双方每隔一段时间便互发一次协议报文,所以当有选中成员链路因为某种原因不能工作时,链路聚合可以很快的感知到,并重设链路状态,置该链路为阻塞状态,流量被重分配给其他选中成员链路。这样就实现了增加带宽,链路动态备份的功能。