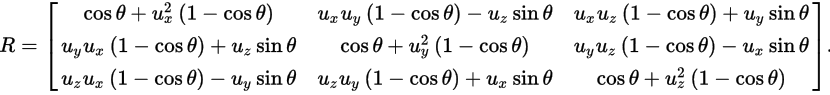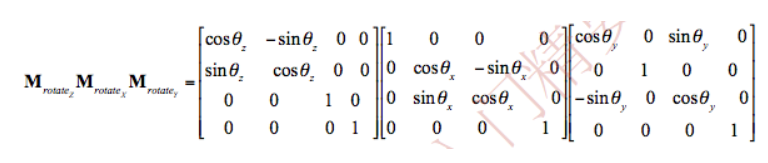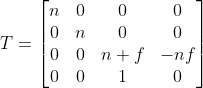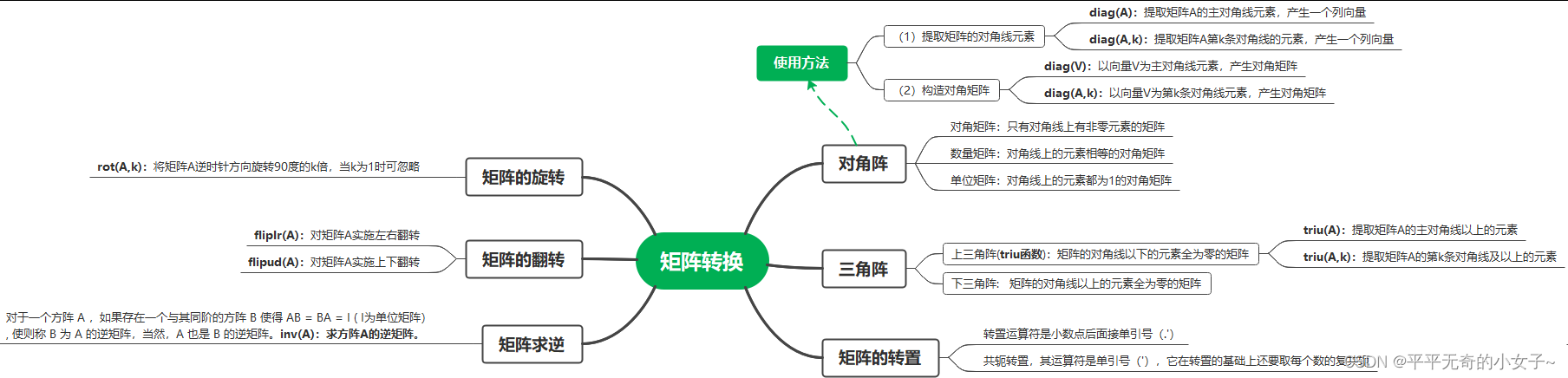
1、对角阵
（1）提取矩阵的对角线元素
>> a = [1:3;4:6;7:9]a =1 2 3 4 5 6 7 8 9 >> diag(a)ans =1 5 9 >> diag(a,1)ans =2 6 >> diag(a,-1)ans =4 8
（2）构造对角矩阵
a = [7 0 1 0 5;3 5 7 4 1;4 0 3 0 2;1 1 9 2 3;1 8 5 2 9]
a =
7 0 1 0 5 3 5 7 4 1 4 0 3 0 2 1 1 9 2 3 1 8 5 2 9
b = diag(1:5)
b =
1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 4 0 0 0 0 0 5
c = b*a *矩阵a左乘对角阵
c =
7 0 1 0 5 6 10 14 8 2 12 0 9 0 6 4 4 36 8 12 5 40 25 10 45
triu(A)：提取矩阵A的主对角线以上的元素；triu(A,k)：提取矩阵A的第k条对角线及以上的元素。
>> a = triu(ones(4))a =1 1 1 10 1 1 10 0 1 10 0 0 1>> a = triu(ones(4),1)a =0 1 1 10 0 1 10 0 0 10 0 0 0>> a = triu(ones(4),-1)a =1 1 1 11 1 1 10 1 1 10 0 1 1
2、矩阵的转置
转置运算符是小数点后面接单引号（.’）；共轭转置，其运算符是单引号（’），它在转置的基础上还要取每个数的复共轭；
实数的转置与共轭转置是一样的
>> a = [1+2i,3;3-5i,2;1-3i,9]a =1.0000 + 2.0000i 3.0000 + 0.0000i3.0000 - 5.0000i 2.0000 + 0.0000i1.0000 - 3.0000i 9.0000 + 0.0000i>> a.'ans =1.0000 + 2.0000i 3.0000 - 5.0000i 1.0000 - 3.0000i3.0000 + 0.0000i 2.0000 + 0.0000i 9.0000 + 0.0000i>> a'ans =1.0000 - 2.0000i 3.0000 + 5.0000i 1.0000 + 3.0000i3.0000 + 0.0000i 2.0000 + 0.0000i 9.0000 + 0.0000i
3、矩阵的翻转
rot(A,k)：将矩阵A逆时针方向旋转90度的k倍，当k为1时可忽略
>> a = [1 2;-3 -5;-5 9]a =1 2-3 -5-5 9>> rot90(a) *旋转90度ans =2 -5 91 -3 -5>> rot90(a,2) *旋转180度ans =9 -5-5 -32 1
fliplr(A)：对矩阵A实施左右翻转；flipud(A)：对矩阵A实施上下翻转
>> a = [1 2 1 1;-3 -5 2 6;-5 9 -9 6;1 3 2 -8;3 2 9 6]a =1 2 1 1-3 -5 2 6-5 9 -9 61 3 2 -83 2 9 6>> fliplr(a) *左右翻转ans =1 1 2 16 2 -5 -36 -9 9 -5-8 2 3 16 9 2 3>> flipud(a) *上下翻转ans =3 2 9 61 3 2 -8-5 9 -9 6-3 -5 2 61 2 1 1
>> a = magic(4) *生成四阶魔方矩阵a =16 2 3 135 11 10 89 7 6 124 14 15 1>> a1 = sum(diag(a)) *主对角线之和a1 =34>> b = fliplr(a) *左右翻转b =13 3 2 168 10 11 512 6 7 91 15 14 4>> b1 = sum(diag(b)) *副对角线之和b1 =34
