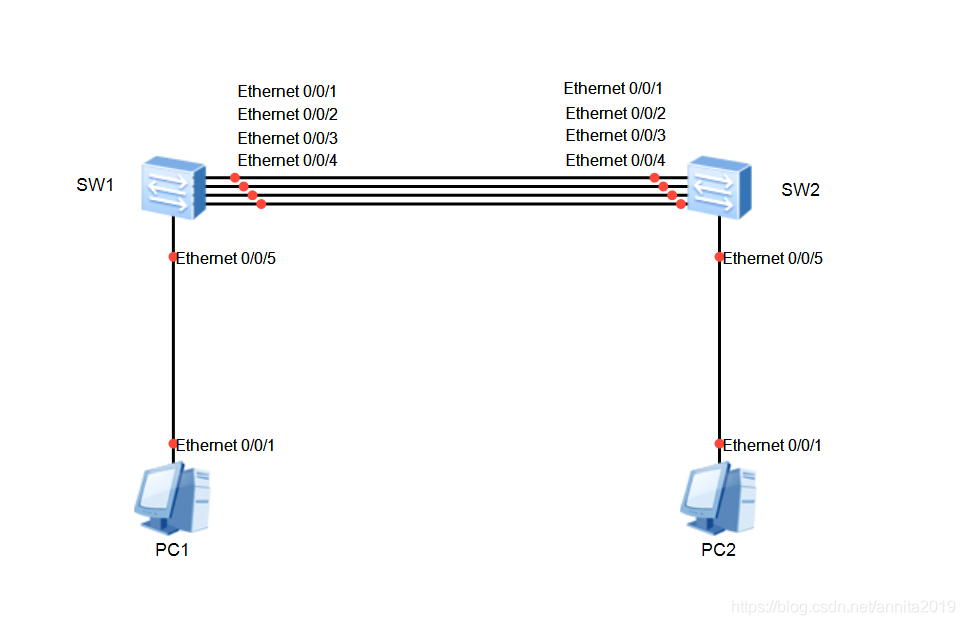
实验拓扑如下:
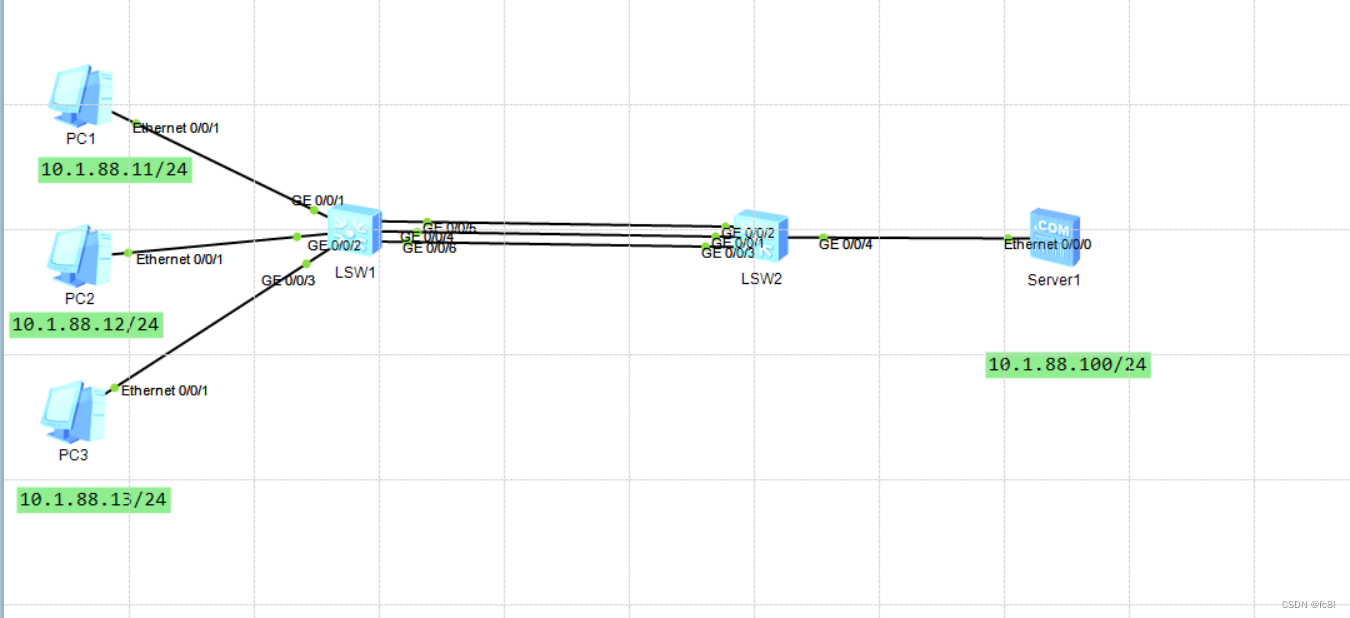
在sw1和sw2上配置手工链路聚合
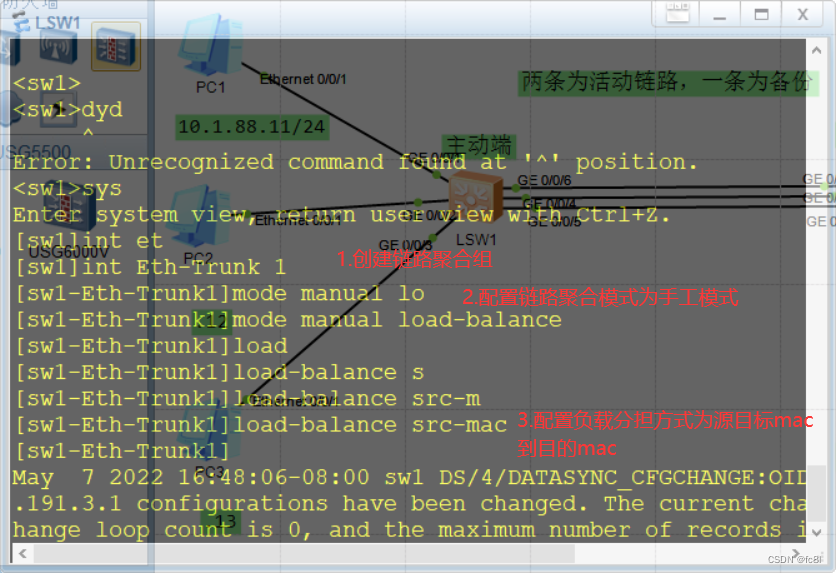 将成员接口放入链路聚合组中,有两种方法:1.在聚合组中添加接口
将成员接口放入链路聚合组中,有两种方法:1.在聚合组中添加接口
2.分别进入接口将他们放入链路聚合组中(sw2)
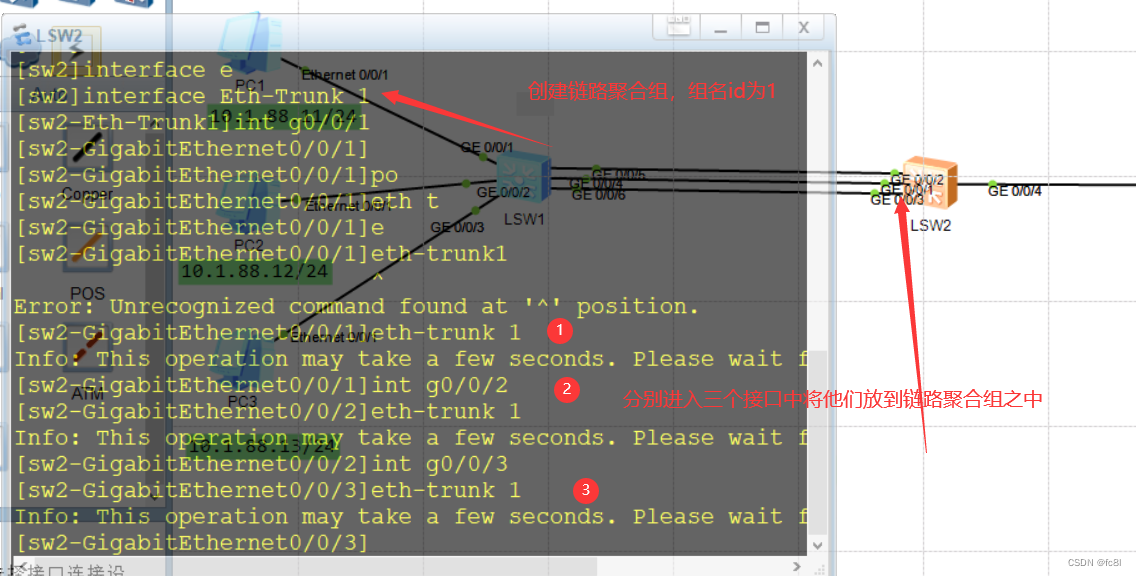
2.在interface g0/0/4中
查看具体配置命令
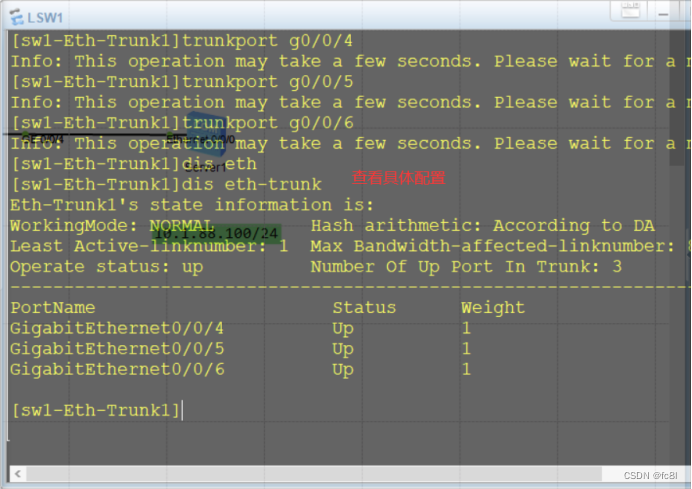
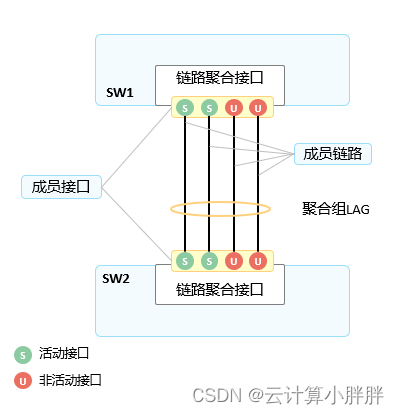
可以看出手工链路聚合是不具有交互的,没有办法看到对端交换机端口启用没有。所以lacp模式提高了链路可靠性。
配置两台交换机手工链路模式之后,我们会发现其实手工模式接口出现问题它是不会发现的,一般情况我们用lacp模式更多一些。配置lacp模式,需要删除之前配置的手工模式。选出sw1为主动端sw2为备份端。在sw1上两条为活动链路,一条为备份链路。
删除手工链路聚合:进入eth-trunk模式下删除成员接口。
interface Eth-Trunk 1 //进入链路聚合组
undo trunkport g0/0/4 //删除成员接口
undo trunkport g0/0/5
undo trunkport g0/0/6
配置完之后,我们要求交换机1和2之间有两条是活动链路,另一条是备份链路,但活动链路出问题的时候,备份链路派上用场。变为活动链路。
设置最大活动链路为两个,
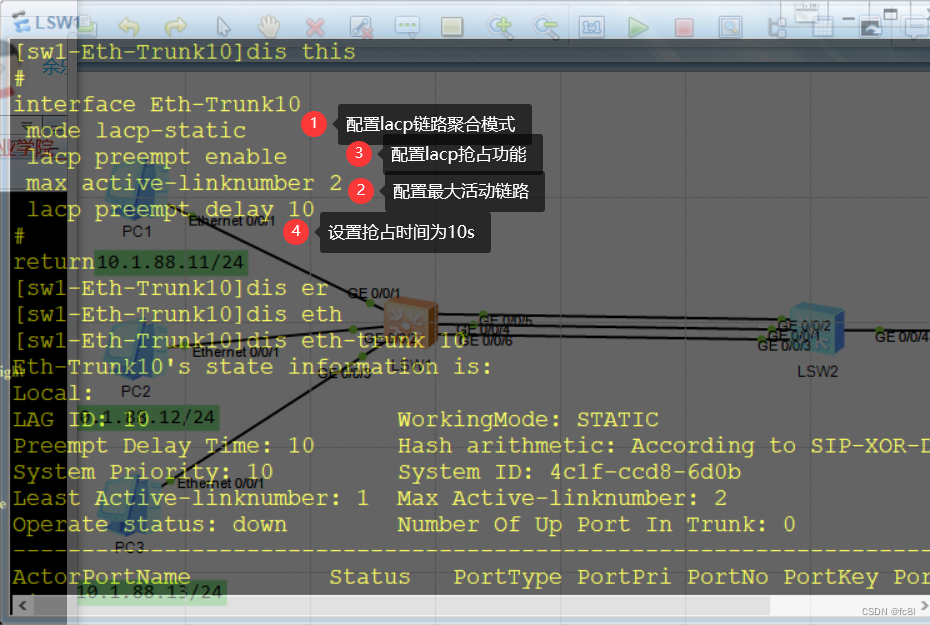
Unselect 表示非活动链路,有活动链路是需要双方的协商。在sw2上也需要配置,sw2是被动端,不需要配置优先级了。
sw2配置如下:首先要删除干净,然后配置lacp链路模式
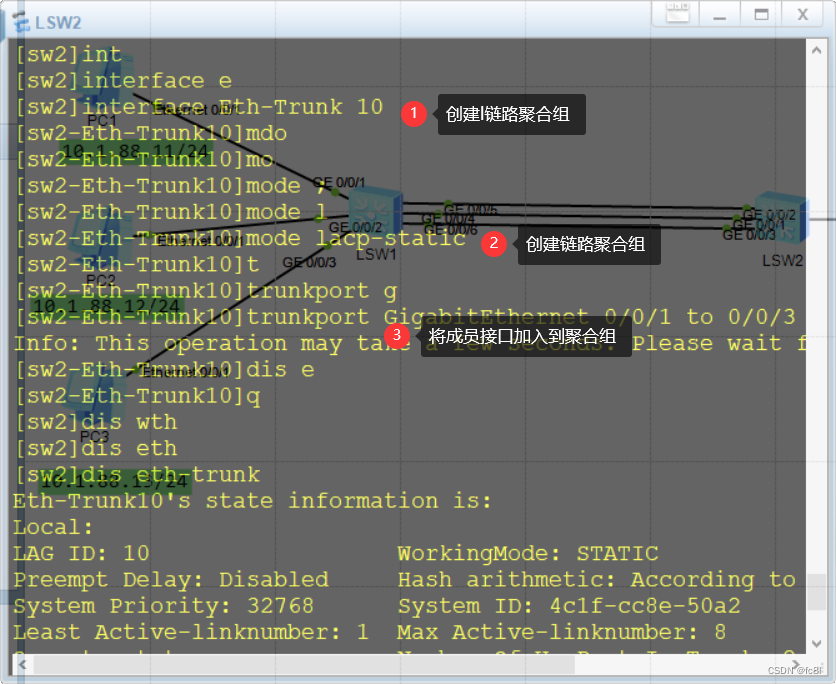
sw2配置完之后,在sw1上查看,g0/0/6是非活动链路状态,我们的要求是要g0/0/5为非活动链路状态。
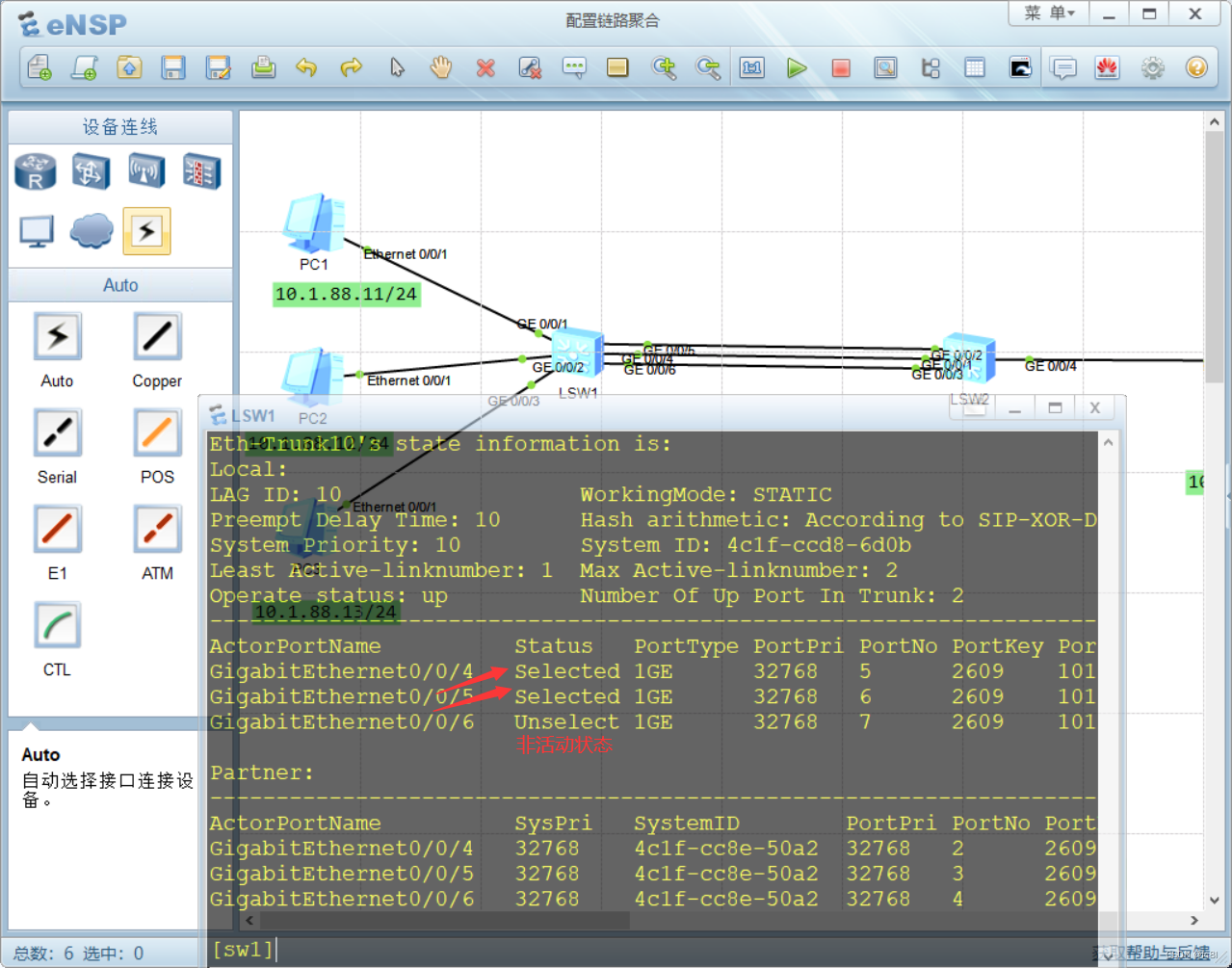
要更改他们的成员接口状态是活动还是非活动也是首先看优先级,同样,值越小,优先级越高。优先级最高的被选作为活动接口。值越小则为非活动端口。
要想让g0/0/5端口作为备份端口,我们可以将它的优先级变大,反则也可以让g0/0/4端口和g0/0/6端口优先级变小
在sw1上做配置,进入到g0/0/5端口更改它的优先级,让它的值变大,这样优先级就变小,就是非活动端口。
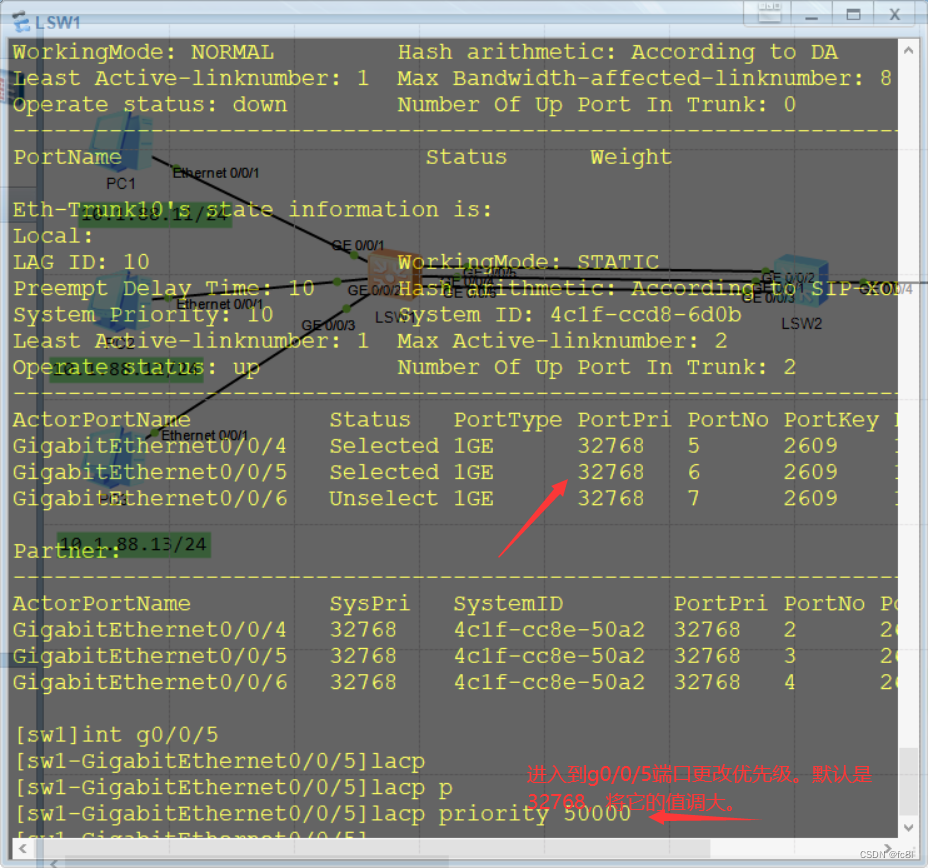
此时再来查看我们发现g0/0/5已经是非活动链路了
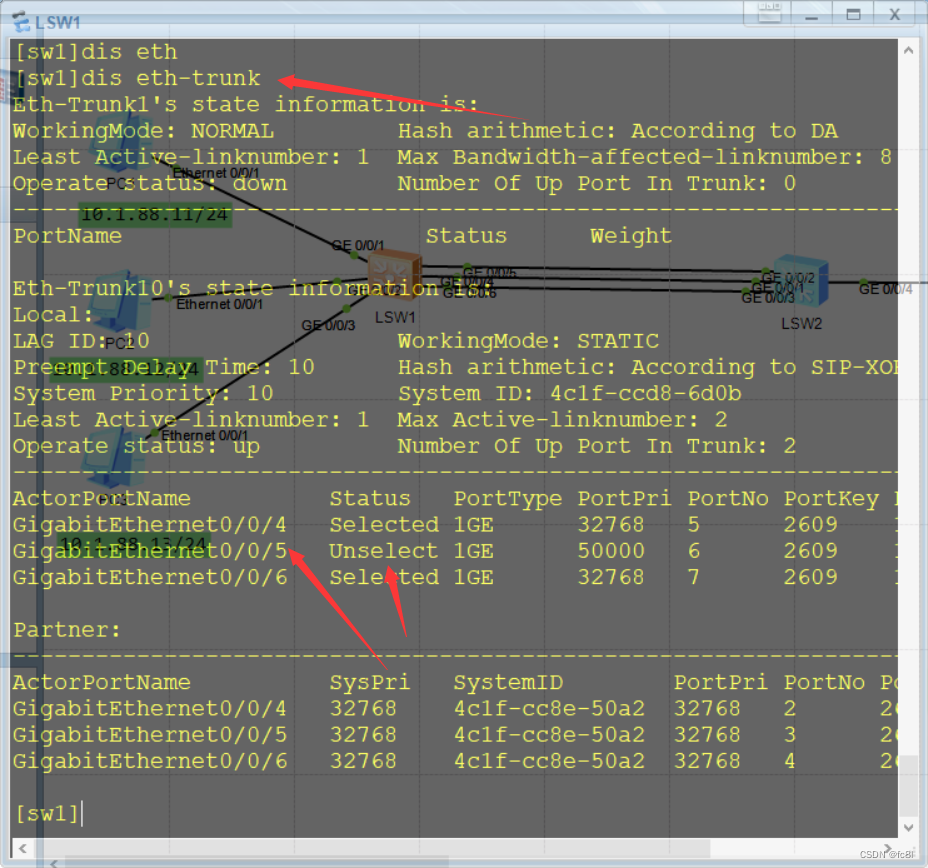
当我们关闭shut g0/0/4端口,那么,非活动链路g0/0/5将顶替g0/0/4变为活动目录。中间有延迟时间,当重新启动g0/0/4 那么g0/0/5仍是非活动链路
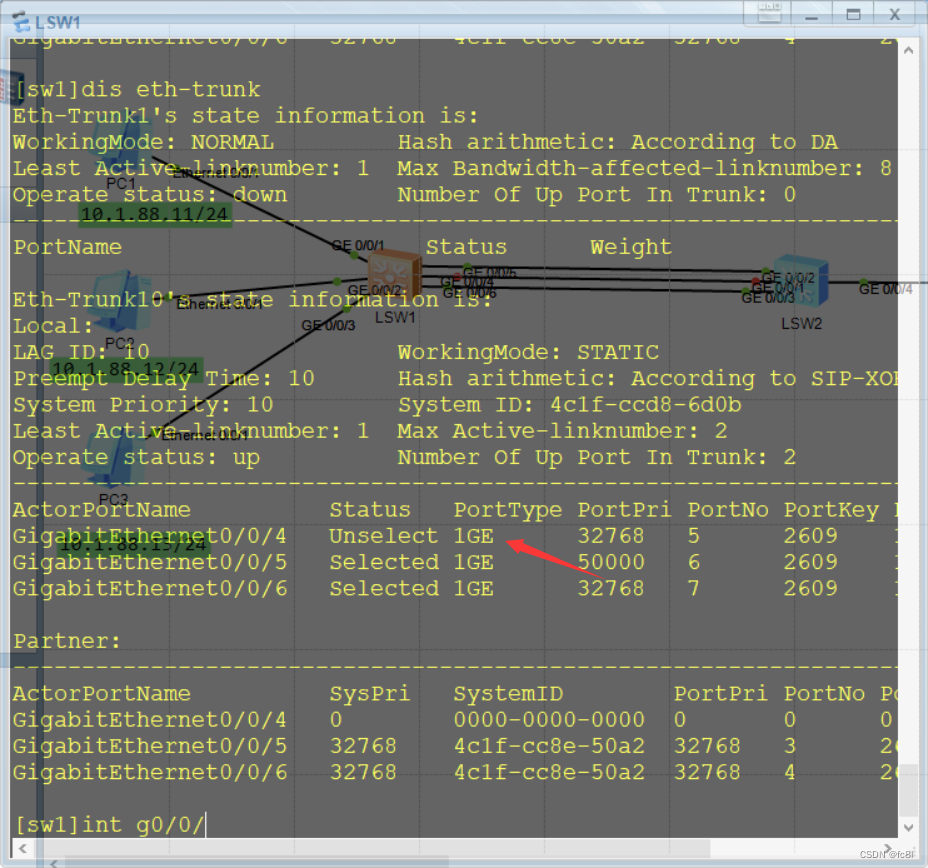
在sw2上对应的是g0/0/1端口出现故障
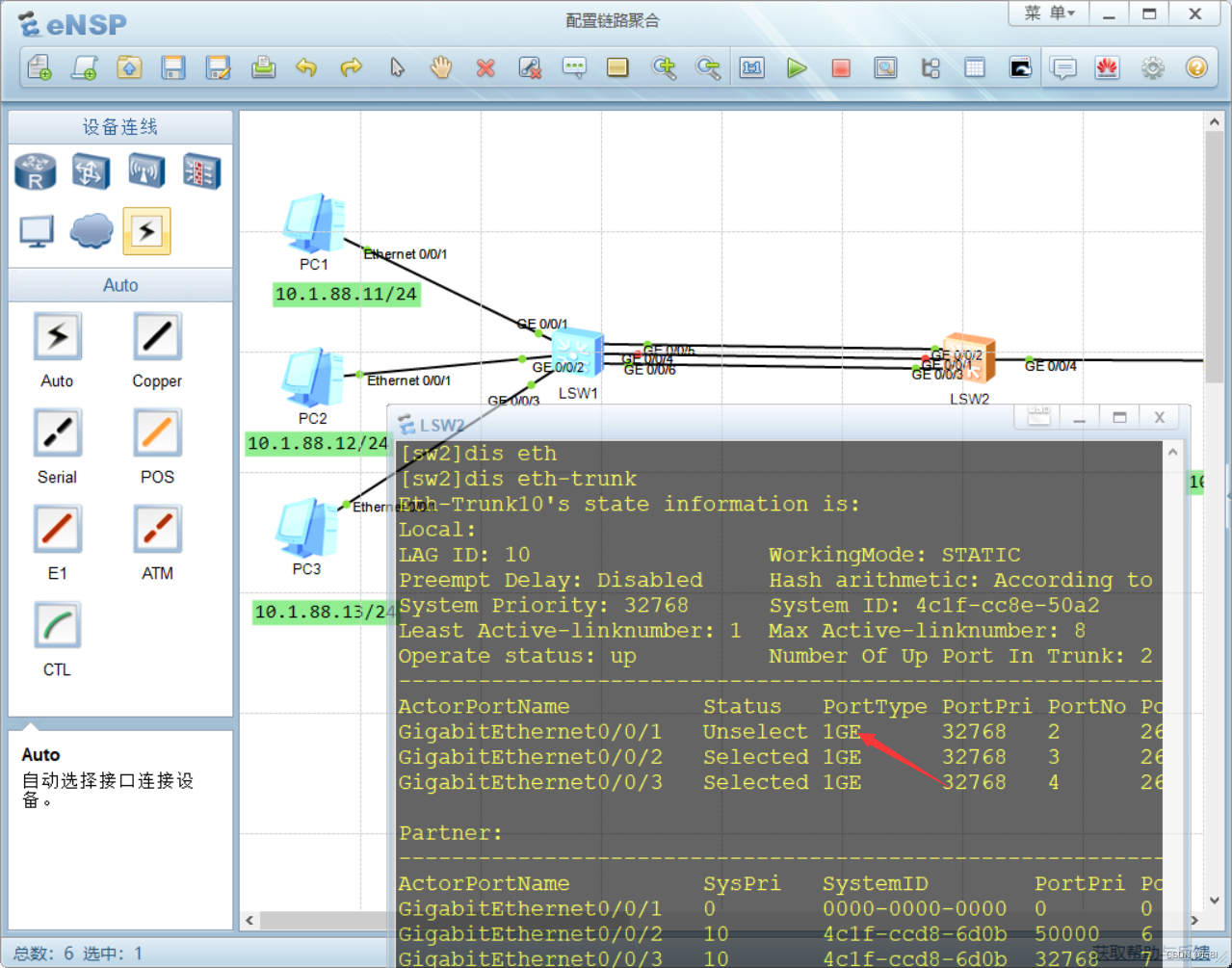
恢复关闭的g0/0/4端口的命令是 undo shut
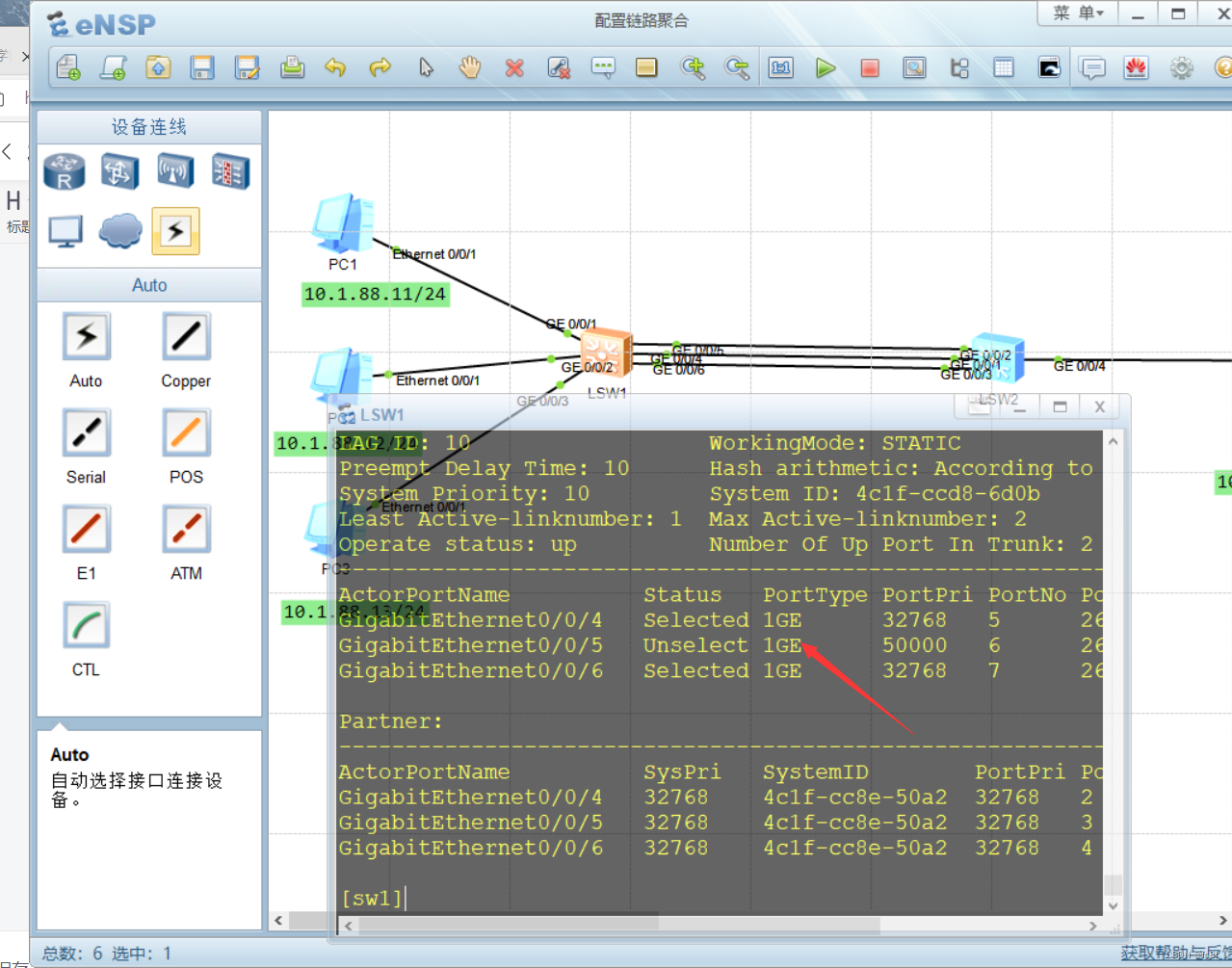
那么这时我们的实验已经做完啦!
知识点总结