一、手动配置链路聚合

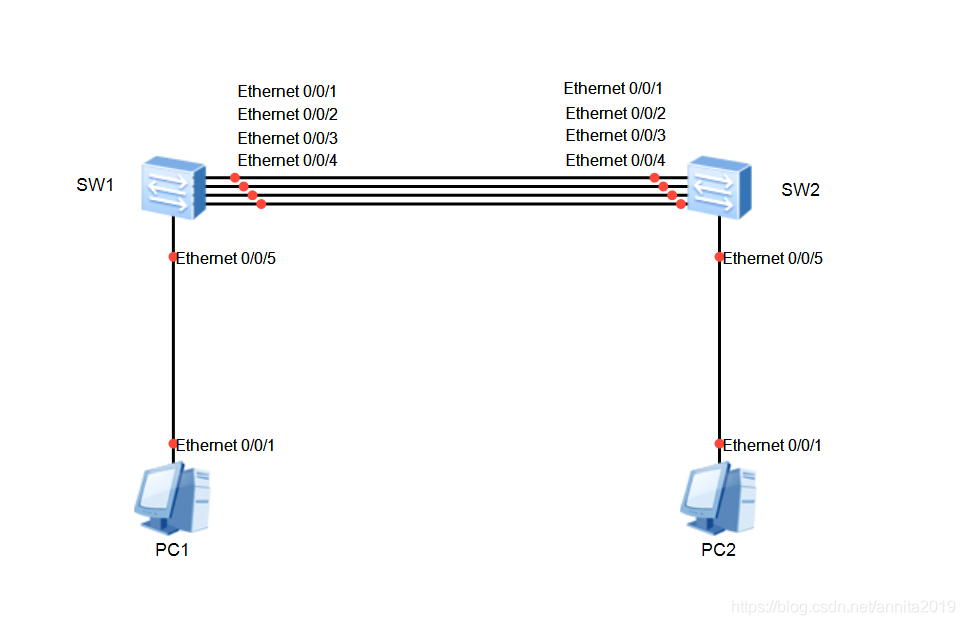
拓扑图

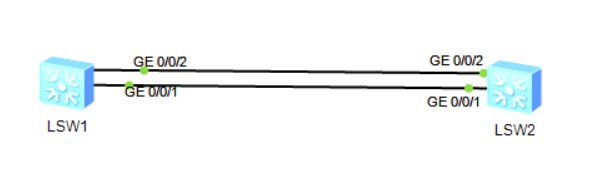
• 要求：通过手动配置交换机SW1和SW2的GE0/0/1、GE0/0/2端口来进行链路聚合。
• 配置过程
  SW1的配置
  
  SW2的配置
  

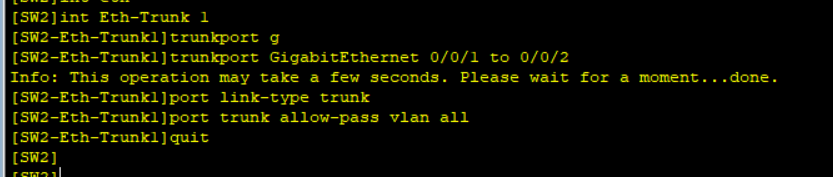
二、LACP配置链路聚合

拓扑图

• 要求：通过LACP配置交换机SW1和SW2的GE0/0/1、GE0/0/2端口来进行链路聚合。
• 配置过程
  SW1的配置
  
  SW2的配置
  
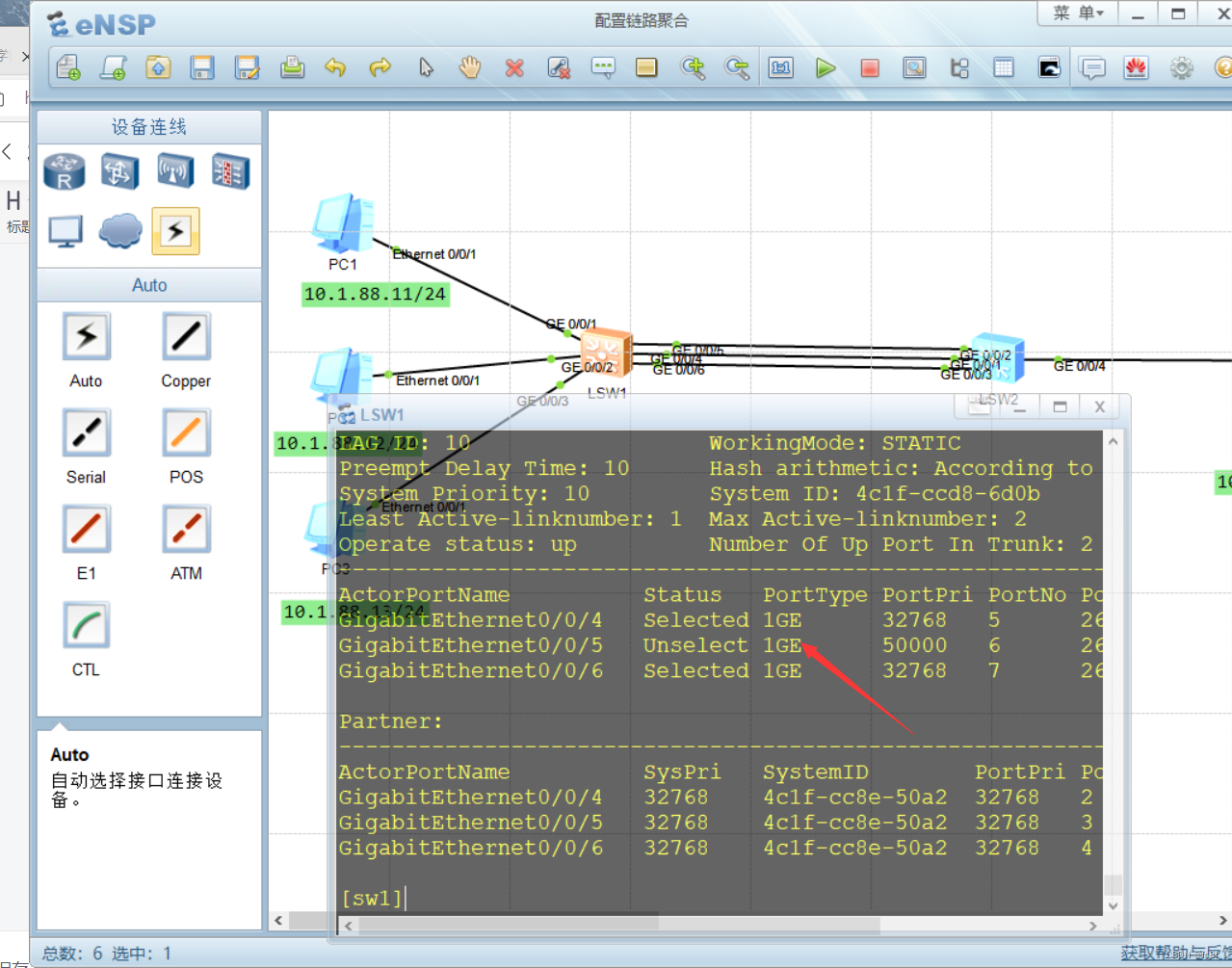
• 检查Eth-Trunk及其成员端口的状态
  

（1）ActorPortName：本地成员端口或对端成员端口的名称。
（2）Status：本地成员端口的状态，在LACP模式下，状态分为Selected（表示端口被选中并成为主要端口）和Unselect（表示端口被选中并成为备用端口）；在手动配置模式下，状态分为Up（表示端口正常）和Down（表示端口出现了物理故障）。
（3）PortType：本地成员端口的类型
（4）PortPri：本地成员端口或者对端成员端口的LACP端口的优先级。

三、LACP系统的优先级

• 在LACP模式下，两端设备的活动端口必须保持一致，这样才能正常建立Eth-Trunk，为了让两端设备动态地确定活动端口，LACP会根据系统优先级确定主动端，并让主动端来选择活动端口。管理员可以手动更改这个参数，优先级的取值是0~65535，默认值为32768，数值越小，优先级越高。在默认情况下，两端优先级相同，此时，会使用系统MAC地址来确定谁是主动端（MAC地址小的为主动端）。
• 配置命令
  
• 查看结果
  
  可以看到系统优先级（System Priority）改成了3000

四、LACP端口的优先级

• 要求，将SW1的GE0/0/1端口优先级设置为1000，GE0/0/2的优先级设置为2000
  
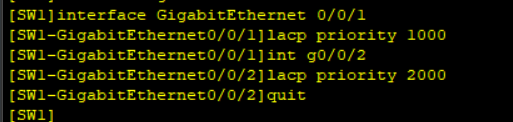
• 查看结果
  

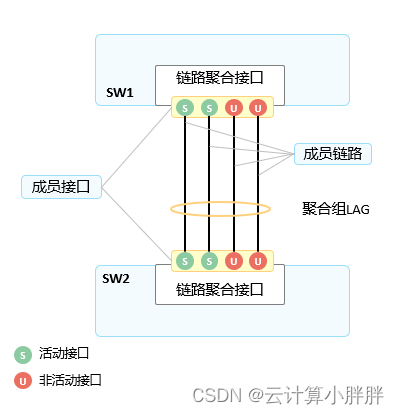
五、Eth-Trunk 中活动端口的数量

• LACP端口优先级的工作与活动端口的数量及LACP的抢占功能相关。在每个Eth-Trunk中，默认的活动端口为8个，管理员可以根据实际需求更改此参数，取值为1~8。
• 实验要求：将Eth-Trunk中的活动端口数量改为1

查看默认的活动端口数量

修改活动端口数量

再次查看

可以看到最大活动端口数量【Max Active-linknumber】为1，而端口的状态也是一个为Selected另一个为Unselect。

• 将SW1的GE0/0/1端口关闭模拟故障
  
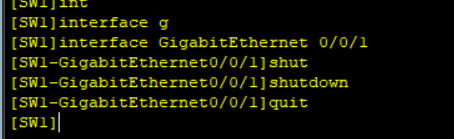
  再次查看结果
  
  可以看到当GE0/0/1Down掉以后，与GE0/0/2的状态互换了

六、LACP抢占功能

• 要想在端口GE0/0/1恢复正常工作后，使交换机SW1自动切换回使用端口GE0/0/1，则需要启用LACP抢占功能。
  
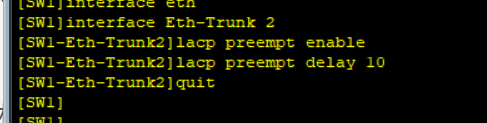
  【lacp preempt enable】开启LACP抢占
  【lacp preempt delay 10】更改抢占延迟时间

• 开启GE0/0/1端口
  

• 查看状态