链路聚合

article/2025/9/15 4:17:43

一.概念

1.端口绑定技术

二.二层链路聚合

1.链路聚合实现的条件

2.拓扑图

三.三层链路聚合

1.拓扑图

总结

一.概念

1.端口绑定技术

链路聚合是将一组物理接口捆绑在一起作为一个逻辑接口来增加宽带的一种方法。又称为多接口负载均衡组或链路聚合组，通过在两台设备之间建立链路聚合组，可以提供更高的通讯带宽和更高的可靠性。链路聚合不仅为设备间提供了冗余保护，而且不需要对硬件进行升级。

二.二层链路聚合

1.链路聚合实现的条件

每个Eth-Trunk接口下最多可以包含8个成员接口。
成员接口不能配置任何业务和静态MAC地址。
成员接口加入Eth-Trunk时，必须为缺省的hybrid类型接口。
Eth-Trunk接口不能嵌套，即成员接口不能是Eth-Trunk。
一个以太网接口只能加入到一个Eth-Trunk接口，如果需要加入其他Eth-Trunk接口，必须先退出原来的Eth-Trunk接口。
一个Eth-Trunk接口中的成员接口必须是同一类型，例如：FE口和GE口不能加入同一个Eth-Trunk接口。
可以将不同接口板上的以太网接口加入到同一个Eth-Trunk。
如果本地设备使用了Eth-Trunk，与成员接口直连的对端接口也必须捆绑为Eth-Trunk接口，两端才能正常通信。
当成员接口的速率不一致时，实际使用中速率小的接口可能会出现拥塞，导致丢包。
当成员接口加入Eth-Trunk后，学习MAC地址时是按照Eth-Trunk来学习的，而不是按照成员接口来学习的。

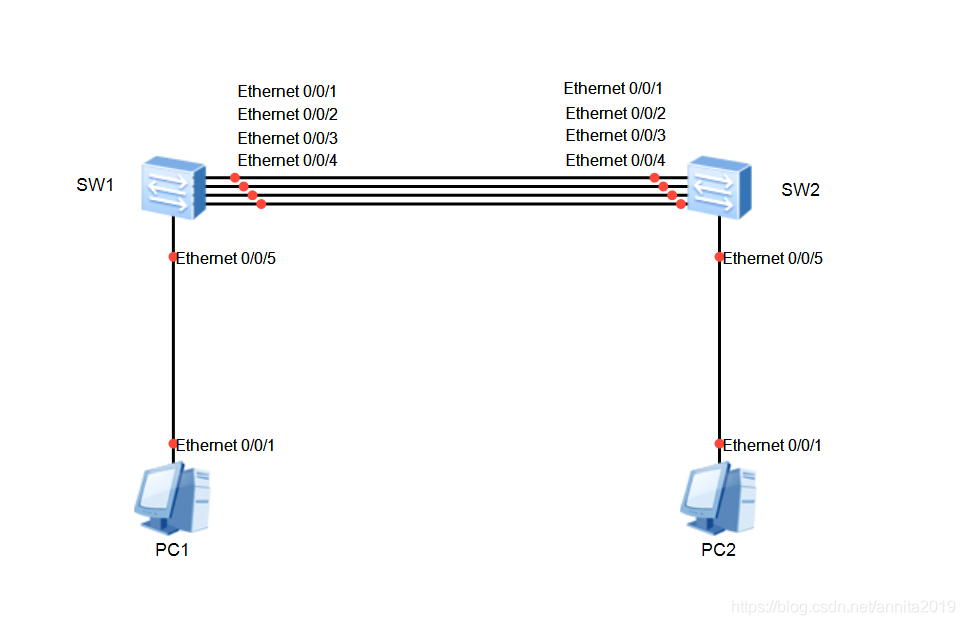
2.拓扑图

端口聚合又称链路捆绑，分为二层和三层链路捆绑。针对二层交换机形成的链路不带IP地址功能。三层链路捆绑针对三层交换机形成的链路带IP地址功能。

第一种

二层交换机

<Huawei>undo terminal monitor 
Info: Current terminal monitor is off.
<Huawei>sys
Enter system view, return user view with Ctrl+Z.
[Huawei]sysname sw1
[sw1]user-interface console 0
[sw1-ui-console0]idle-timeout 0 0
[sw1-ui-console0]q
[sw1]int Eth-Trunk 1
[sw1-Eth-Trunk1]int e0/0/1
[sw1-Ethernet0/0/1]eth-trunk 1
[sw1-Ethernet0/0/1]int e0/0/2
[sw1-Ethernet0/0/2]eth-trunk 1
[sw1-Ethernet0/0/2]int e0/0/3
[sw1-Ethernet0/0/3]eth-trunk 1
[sw1-Ethernet0/0/3]int e0/0/4
[sw1-Ethernet0/0/4]eth-trunk 1
[sw1-Ethernet0/0/4]q
[sw1]display eth-trunk 1

pc2 ping pc1能ping通

第二种划分vlan的

<Huawei>undo terminal monitor 
Info: Current terminal monitor is off.
<Huawei>sys
Enter system view, return user view with Ctrl+Z.
[Huawei]sysname sw1
[sw1]user-interface console 0
[sw1-ui-console0]idle-timeout 0 0
[sw1-ui-console0]q
[sw1]int Eth-Trunk 1
[sw1-Eth-Trunk1]int e0/0/1
[sw1-Ethernet0/0/1]eth-trunk 1
[sw1-Ethernet0/0/1]int e0/0/2
[sw1-Ethernet0/0/2]eth-trunk 1
[sw1-Ethernet0/0/2]int e0/0/3
[sw1-Ethernet0/0/3]eth-trunk 1
[sw1-Ethernet0/0/3]int e0/0/4
[sw1-Ethernet0/0/4]eth-trunk 1
[sw1-Ethernet0/0/4]q
[sw1]display eth-trunk 1
[sw1-Ethernet0/0/4]q
[sw1]vlan 2
[sw1-vlan2]int e0/0/5
[sw1-Ethernet0/0/5]port link-type access
[sw1-Ethernet0/0/5]port default vlan 2
[sw1-Ethernet0/0/5]q
[sw1]int Eth-Trunk 1
[sw1-Eth-Trunk1]port link-type trunk 
[sw1-Eth-Trunk1]port trunk allow-pass vlan 2
[sw1-Eth-Trunk1]q

pc1 ping pc2能ping通

三.三层链路聚合

eth-trunk接口一旦选择在三层是不能配置trunk/access类型的

1.拓扑图

SW1
<HUAWEI>u t m
[~HUAWEI]sysname sw1
[~sw1]user-interface console 0
[~sw1-ui-console0]idle-timeout 1440
[*sw1]int Eth-Trunk 1
[*sw1-Eth-Trunk1]undo portswitch 
[*sw1-Eth-Trunk1]ip add 10.1.1.1 24
[*sw1]int g1/0/0
[*sw1-GE1/0/0]undo shutdown
[*sw1-GE1/0/0]eth-trunk 1
[*sw1-GE1/0/0]int g1/0/1
[*sw1-GE1/0/1]undo shutdown 
[*sw1-GE1/0/1]eth-trunk 1
[*sw1-GE1/0/1]int g1/0/2
[*sw1-GE1/0/2]undo shutdown 
[*sw1-GE1/0/2]eth-trunk 1
[*sw1-GE1/0/2]undo shutdown 
[*sw1-GE1/0/2]int g1/0/3
[*sw1-GE1/0/3]undo portswitch
[*sw1-GE1/0/3]undo shutdown
[*sw1-GE1/0/3]ip add 192.168.1.1 24
[*sw1]ip route-static 192.168.2.0 24 10.1.1.2
<sw1>save  最后一定要save保存一下

SW2
<HUAWEI>u t m 
<HUAWEI>sys
[~HUAWEI]sysname sw2
[~sw2]user-interface console 0
[~sw2-ui-console0]idle-timeout 1440
[*sw2]int Eth-Trunk 1
[*sw2-Eth-Trunk1]undo portswitch 
[*sw2-Eth-Trunk1]ip add 10.1.1.2 24
[*sw2-Eth-Trunk1]int g1/0/0
[*sw2-GE1/0/0]undo shutdown
[*sw2-GE1/0/0]eth-trunk 1
[*sw2-GE1/0/0]int g1/0/1
[*sw2-GE1/0/1]undo shutdown 
[*sw2-GE1/0/1]eth-trunk 1
[*sw2-GE1/0/1]int g1/0/2
[*sw2-GE1/0/2]undo shutdown 
[*sw2-GE1/0/2]eth-trunk 1
[*sw2-GE1/0/2]int g1/0/3
[*sw2-GE1/0/3]undo portswitch 
[*sw2-GE1/0/3]undo shutdown 
[*sw2-GE1/0/3]ip add 192.168.2.2 24
[*sw2]ip route-static 192.168.1.0 24 10.1.1.1
<sw2>save