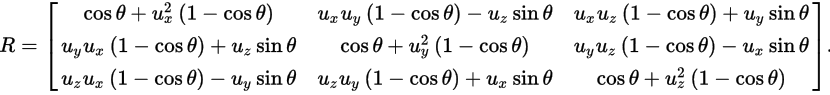【线性代数】理解矩阵变换及行列式的本质

article/2025/9/15 4:12:29

参考：行列式的本质是什么？

这篇文章的结构是：

线性变换的几何直观
实现线性变换的矩阵
行列式

一、线性变换的几何直观

线性变换的几何直观有三个要点：

变换前是直线的，变换后依然是直线
直线比例保持不变
变换前是原点的，变换后依然是原点

比如说旋转：

比如说推移：

这两个叠加也是线性变换：

二、实现线性变换的矩阵

矩阵可以讲的东西非常多，这里通过一个具体的例子来展示下矩阵是如何完成线性变换的。

把基画出来的原因是因为矩阵变换的其实是基。

举例子来看看，比如旋转（旋转矩阵 $T_{rotate} = \begin{bmatrix} cos(\theta) & -sin(\theta)\\ sin(\theta)& cos(\theta) \end{bmatrix}$ ）：

如果要说详细点，实际上：

在参考文章中有一个可操作实例，建议去操作一下，以加深印象。

再给一个例子，看看推移是怎么改变基的：

三、行列式

3.1 行列式是线性变换的伸缩因子（负值为反向收缩），准确来讲缩放的倍数为 $\sqrt{det(A)}$

我们还是拿旋转矩阵来举例子：

什么意思？我们来看看：

在原文中，依旧有一个可操作的实例，可以感受不同行列值大小对线性变换所带来的影响。

掌握了行列式是线性变换的伸缩因子这一点之后，我们就很容易理解各种行列式的值与线性变换的关系。

3.2 行列式大于0，以下记线性变换矩阵为 $A$

1、 $det(A) >1$ ，很显然对于图形有放大的作用：

2、 $det(A) = 1$ ，图形的大小不会变换：

3、 $0<det(A) < 1$ ，很显然对于图形有缩小的作用：

3.3 $det(A) = 0$

行列式等于0，有一个重要的结论是，矩阵不可逆。这点也很好理解。

先看看什么是可逆。原始的图形是这个样子：

通过旋转矩阵，逆时针旋转 ${45}^{\circ}$ ：

再通过另外一个旋转矩阵，顺时针旋转 ${45}^{\circ}$ ：

看起来这个正方形就像没有变换过一样，因此 $\begin{bmatrix} cos(-{45}^{\circ}) & -sin(-{45}^{\circ})\\ sin(-{45}^{\circ})& cos(-{45}^{\circ}) \end{bmatrix}$ 和 $\begin{bmatrix} cos({45}^{\circ}) & -sin({45}^{\circ})\\ sin({45}^{\circ})& cos({45}^{\circ}) \end{bmatrix}$ 互为逆矩阵。

有的线性变换是可逆的，有的不行，比如 $det(A)=0$ 这样的线性变换就是不可逆的。从图像上看，图形会缩成一点或者一个超平面：

或者缩成一条直线：

没有矩阵可以把它们恢复成原来的样子。

这就好比摔碎的鸡蛋、泼出去的水、破了的镜子：

所谓覆水难收、破镜难圆就是这个意思。

3.4 $det(A) < 0$

原始图像是这样的：

被 $det(A) < 0$ 的矩阵线性变换后是这样的：

$det(A) < 0$ ，其实就是改变了基的“左右手法则”。

四、推论

1、矩阵乘法与行列式乘法

知道了行列式的意义，我们就很容易知道，为什么说：

稍微解释一下，矩阵乘法之所以不成立，本质上是因为——矩阵 $T_1,T_2$ 都代表在基 $I$ 下的线性变换，虽然直观上理解 $T_1T_2$ 与 $T_2T_1$ 都做了同样的线性变换，只是顺序不同并不应该影响结果。但实际上，我们必须要注意一点，即虽然矩阵都是 $T_1$ 或者 $T_2$ 的形式，但变换的形式是相对于基而言的，同一个线性变换矩阵在不同基下进行的线性变换实际上是不同的。（更详细的理解可以参考相似矩阵）

即对于 $T_1T_2$ ，先在基 $I$ 下进行 $T_2$ 的线性变换，然后再在基 $T_2\times I=T_2$ 下进行 $T_1$ 的线性变换。此时的变换 $T_1$ 进行的操作（如推移或旋转）实际上是不等同于在基 $I$ 下进行的 $T_1$ 变换的。

对于 $T_2T_1$ 同理也可以这么理解，最后就显而易见矩阵乘法的交换率是不成立的。

但在某些特殊情况下，矩阵乘法的交换律依旧成立。

(1) 设A , B 至少有一个为零矩阵,则A , B 可交换;

(2) 设A , B 至少有一个为单位矩阵, 则A , B可交换;

(3) 设A , B 至少有一个为数量矩阵（ $kI$ ）则A , B可交换;

(4) 设A , B 均为对角矩阵,则A , B 可交换;

(5) 设A , B 均为准对角矩阵（准对角矩阵是分块矩阵概念下的一种矩阵。即除去主对角线上分块矩阵不为零矩阵外，其余分块矩阵均为零矩阵）,且对角线上的子块均可交换，则A , B 可交换;

还有一种情况就是二维矩阵的旋转变换。但三维及以上就不成立了。

第二点是行列式乘法。经过上面的一堆介绍，至少可以明白矩阵行列式是线性变换的伸缩因子，方阵线性变换由三部分组成——推移、旋转、伸缩。行列式的值表示了伸缩的比例，不论是 $T_1T_2$ 还是 $T_2T_1$ ，其伸缩结果都是（设原基向量的长度为 $l$ ） $l* det(T_1) *det(T_2) = l* det(T_2) *det(T_1)$ 。