MS酋长昨天已经分享了Win10重置Linux子系统教程，可以用来解决Linux子系统无法正常运行等问题。那么如果是我们忘记了Linux子系统用户的密码，虽然也可以通过重置Linux子系统再重设用户名和密码来解决，但之前用户的数据和设置均会丢失。所以，我们不必如此大动干戈，只需重置用户密码即可，该用户的数据和设置能得以保留。重置密码的方法如下：

步骤一：把Linux子系统默认用户设置为root

打开cmd命令提示符或Windows PowerShell，运行以下命令：

Ubuntu config --default-user root

PS: 请把Ubuntu更换成你实际安装的Linux发行版名称

步骤二：运行Linux子系统重置密码

这时你再运行Linux子系统(例如Ubuntu)，就会默认以root用户登录了。运行命令：

passwd 需要重置密码的用户名

例如：

passwd mschief

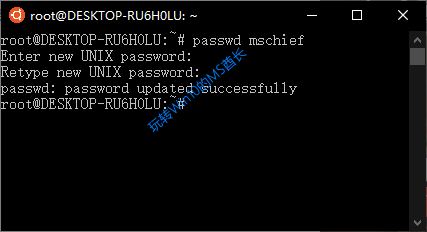
这时Linux子系统就会提示我们输入新密码，和以前一样，输入密码时是没有任何显示的。然后按照提示再输入一遍新密码。这时Linux子系统会提示密码更新完成。

步骤三：把Linux子系统默认用户更改为已重置密码的用户

重置密码之后，我们就可以使用该用户登录Linux子系统了。所以，我们还要再把Linux子系统默认用户由root更改为已重置密码的用户。

cmd命令提示符或Windows PowerShell，运行以下命令即可：

Ubuntu config --default-user mschief

然后我们再运行Linux子系统，就会发现已经使用该用户登录了。

相关内容

相关文章