PART.0 Mandelbrot 介绍

“无规则的碎片” “魔鬼的聚合物” “上帝的指纹”

Mandelbrot集合有着多种称谓，那么什么是曼德勃罗特集？Mandelbrot集合可以用复二次多项式：

$$f_c(z)=z^2+c$$

来表示，其中c是一个复数。对于每一个c，从z=0,开始对$f_c(z)$进行迭代。序列:

$$(0,f_c(0),f_c(f_c(0)),f_c(f_c(f_c(0))),\dots )$$

的元素的模或者延伸到无穷大，或者只停留在有限半径的圆盘内。Mandelbrot集合就是使以上序列不延伸至无限大的所有c点的集合。

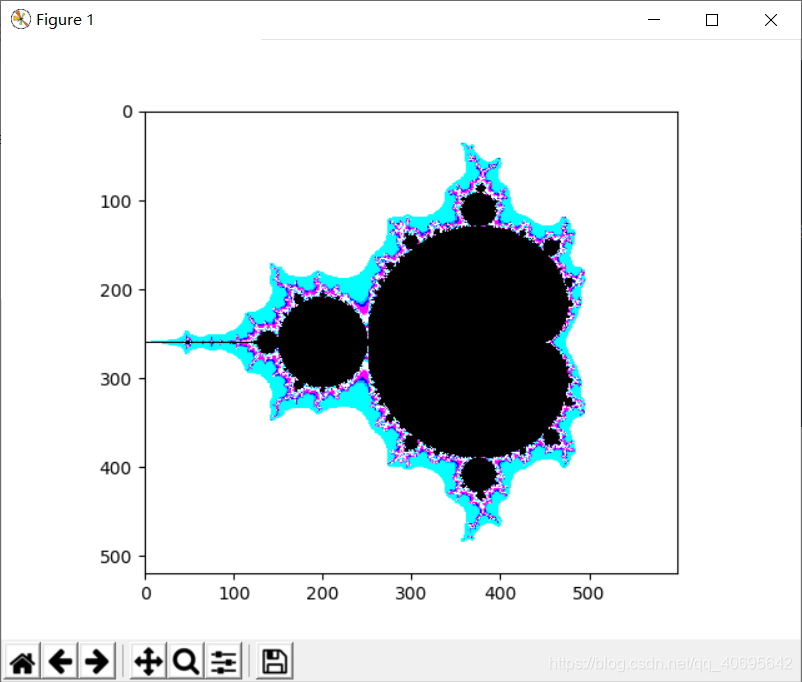
在复平面上，将所有属于Mandelbrot集合的点标记为黑色，将所有不属于集合的点按照其发散速度赋予不同的颜色，就可以得到Mandelbrot的经典图像：

从图像Mandelbrot集合的边缘无限放大，可以不断看到各种各样的分形结构，注意这里图上的标号，会和后面的各个例子一一对应。这里先给出这个全貌图的绘制代码(此代码参考mathworks官网)：

maxIterations=800;
gridSize=1000;
xlim=[-2 1];
ylim=[-1.5 1.5];% Setup
x=linspace(xlim(1),xlim(2),gridSize);
y=linspace(ylim(1),ylim(2),gridSize);
[xGrid,yGrid]=meshgrid(x,y);
z0=xGrid+1i*yGrid;
count=ones(size(z0));% Calculate
z=z0;
for n=0:maxIterationsz=z.*z+z0;inside=abs(z)<=2;count=count+inside;
end
count=log(count);% Show
imagesc(x,y,count);
colormap([flipud(pink());0 0 0]);

PART.2 不同区域的渲染图

区域4附近：Valley of the Seahorses

x=-0.748766710846959

y=0.123640847970064

区域5附近：West Wing

x=-1.6735

y=0.0003318

区域1附近：Triple Spiral Valley

xlim=[-0.090,-0.086]

ylim=[0.654,0.657]

区域9附近：microbugs

x=-1.7497591451303665

y=-0.0000000036851380

换个颜色，并调整为正方形：

再换个颜色：

区域12附近：Elephant Valley

xlim=[0.275, 0.28]

ylim=[0.006, 0.01]

PART.3 滚动颜色

介绍一个有趣的函数：spinmap

即为滚动颜色，在程序最后面加入：

spinmap(10)

就能让颜色整体轮换滚动10秒

这里图片超出上传大小就不在这放了，想看动图可以点击文末公众号名片去公众号查看

完整代码：

【链接】：https://pan.baidu.com/s/1me67-hxJbwmJYQIHz-3DtQ?pwd=slan

【提取码】：slan