最近要交并行计算的作业了，这周终于把作业写了个大概，这期间感觉学了不少东西，总结一下。
Mandelbrot Set 背景
前几天逛维基百科的时候看到了如下的消息：著名数学家、分形之父Benoît B. Mandelbrot（中文名本华·曼德博）美国时间10月15日辞世，享年85岁。
“1979年，在哈佛大学作为访问学者的期间，曼德博开始研究分形集之一——在复平面上一定变换下具有不变性的朱利亚集合。在加斯顿·朱利亚和皮埃尔·法图学术成果的基础上，曼德博利用公式 fc(z) = z2 + c 反复迭代，在计算机上作出了朱利亚集合的图形。在研究朱利亚集合的拓扑结构是怎样依赖于复参数μ的同时，他还提出了后来一他的名字命名的曼德博集合（曼德博集合今天常常由 z2 + c 定义，因此曼德博早期以μ为参数所作的图像与后来以 c 为参数所得图像恰如镜面反射般左右对称）。”—From Wikipedia
Wikipedia上Mandelbrot的定义为：
曼德博集合可以用复二次多项式
-
来定义
其中c是一个复参数。对于每一个c，从
开始对fc(z)进行迭代。
序列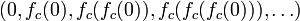 
的值或者延伸到无限大，或者只停留在有限半径的圆盘内。
曼德博集合就是使以上序列不延伸至无限大的所有c点的集合。
公式为：
where 
从数学上来讲，曼德博集合是一个复数的集合。一个给定的复数c或者属于曼德博集合M，或者不是。
要记住上面介绍的最后一句话：Mandelbrot Set是一个集合，谁的集合？是关于当中复数c的集合。刚开始我就老搞不明白Mandelbrot Set和Julia Set的区别，其实他们虽然迭代式大体相同，但是所表示的集合范围却是两码事，下面给出Julia Set的定义：
朱利亚集合可以由下式进行反复迭代得到：
- fc(z) = z2 + c
对于固定的复数c，取某一z值（如z = z0），可以得到序列
这一序列可能反散于无穷大或始终处于某一范围之内并收敛于某一值。我们将使其不扩散的z值的集合称为朱利亚集合。
这里需要注意的是：这个迭代式当中，复数c的值是固定的，而Julia的集合的范围是关于z值的范围。
简单来说，对于迭代式：fc(z) = z2 + c ，Mandelbrot Set 迭代过程中的z值是固定的，是使上述迭代式始终在某一范围内而不发散于无穷大的c值的集合；而Julia Set的迭代过程中c是固定的，上述是使上述迭代式始终在某一范围内而不发散于无穷大的z值的集合。
理解了这些定义，就很容易通过编程来实现这样的集合。
最后就是关于绘图着色的问题，大部分都是通过让||z||>R的迭代次数来决定所绘制的颜色，我们定义如果在最大迭代次数N内没有超过R的集合的颜色为黑色，当最大的迭代次数N足够大时，可以认为这些点属于Mandelbrot Set，具体要多大？理论上来说当N为无穷大时，我们绘制的Mandelbrot Set才是真的符合定义，但是我们即使借助于计算机，也不可能处理这种无限的问题。所以说我们定义在最大迭代次数N之内z的模不超过R就认为就是属于Mandelbrot Set其实是不严格的，所幸的是如果z不属于Mandelbrot Set的时候，||z||的增长速度是非常的快，再加上我们一般电脑的屏幕分辨率的限制，当N值足够大的时候所显示的图像与N趋于无穷时显示的图像几乎没有区别。所以N值只要取足够大就可以了。还有一个问题就是R的大小的选择，我查阅了相关的资料，也没仔细看，相关的证明公式太多，懒得看，直接上结论：“If the absolute value of Z (that is, its distance from 0+0i) ever gets bigger than 2, it will never return to a place closer than 2, but it will actually rapidly escape to infinity.”也就是说如果z的模值大于2的时候，可以证明经过上述公式的迭代，z的模值会很快趋于无穷大。所以现在基本都是取R=2。
所以，经过上述的一番理论知识，我们用绘图的方法来展示Mandelbrot Set只是一种演示，并不完全符合Mandelbrot Set的定义，但是对于展示这个集合的相关特性，已经足够了。
刚开始我定义迭代次数n>N时，为黑色，属于Mandelbrot Set，对于不属于Mandelbrot Set的，我还是通过迭代次数n来决定其颜色，当n从N到N/2时，颜色从黑变红，当n从N/2到0时，颜色从红到白，结果出现如下后果，十分血腥。。。
然后我到网上搜索了相关的配色，最后在Rocky Mountain College的K. Stuart Smith 教授那里找到了一份配色的方案，他是将最大迭代次数设为256，应该是和256色有关，但是具体的色彩算法我也不是很清楚，不过他应该是用的一种叫HSB的配色方案，他写的函数就是将HSB的颜色转换为RGB的，具体代码如下：
1: void setHSBColor (float hue, float saturate, float bright) {
2: // when I wrote this, openGL only liked colors specified by RGB values. The
3: // mandelbrot routine generated an HSB color, so I wrote this routine to do
4: // the conversion. It sure isn't perfect, but it does a respectable job.
5: //
6: // I expect that part of this work (but the final openGL call) could be
7: // pushed back with the mandelbrot color generator for more speedup.
8: //
9: float red, green, blue;
10: float h = (hue * 256) / 60;
11: float p = bright * (1 - saturate);
12: float q = bright * (1 - saturate * (h - (int)h));
13: float t = bright * (1 - saturate * (1 - (h - (int)h)));
14: 15: switch ((int)h) {
16: case 0:
17: red = bright, green = t, blue = p; 18: break;
19: case 1:
20: red = q, green = bright, blue = p; 21: break;
22: case 2:
23: red = p, green = bright, blue = t; 24: break;
25: case 3:
