前言

这段时间看了一个关于维度的视频介绍，叹于其惊艳的多维几何体和分形的视觉动画效果。其实关于分形，已经有很成熟的分形软件和应用场景，可以参看目前流行的分形软件一览，不过没有及时更新，有些链接已经进不了，还有一个 分形艺术网。
关于分形视频的制作，有不同的制作办法，例如，这位仁兄的作品：他的思路是通过Shader渲染，然后通过ffmpeg命令把图片生成mp4视频；也可以通过专业的分形软件来做也可以在分形软件基础上定制开发；本文采用纯Python实现，借助MoviePy这个包来生成视频或者gif动画，本文只是提供有兴趣的朋友，了解这个领域，并可以动手实践体验。
本文讨论范围局限在 Mandelbrot集合和Julia集合。

Mandelbrot集合

如果英语还行，建议去维基百科读英文 Mandelbrot集合

Mandelbrot集合是一个复数c的集合，c由 $z_{n+1}=z_n^2+c$公式在$z_0=0$开始迭代而得到。得到的值可以组成一个数列，依次为 $c,c^2+c,(c^2+c{)}^2+c$……。当该数列发散到无穷时，对应的点就属于Mandelbrot集合。Mandelbrot集合是分形中最经典例子。

如 $c=0$ 时，显然数列永远是0，并不发散，因此 $c=0$ 不属于Mandelbrot集合。

又如$c=3i$ 时，对应的数列为$3i,-9+3i,63-51i,1431-6477j$ …. ，数字越来越庞大，因此3i就属于Mandelbrot集合。

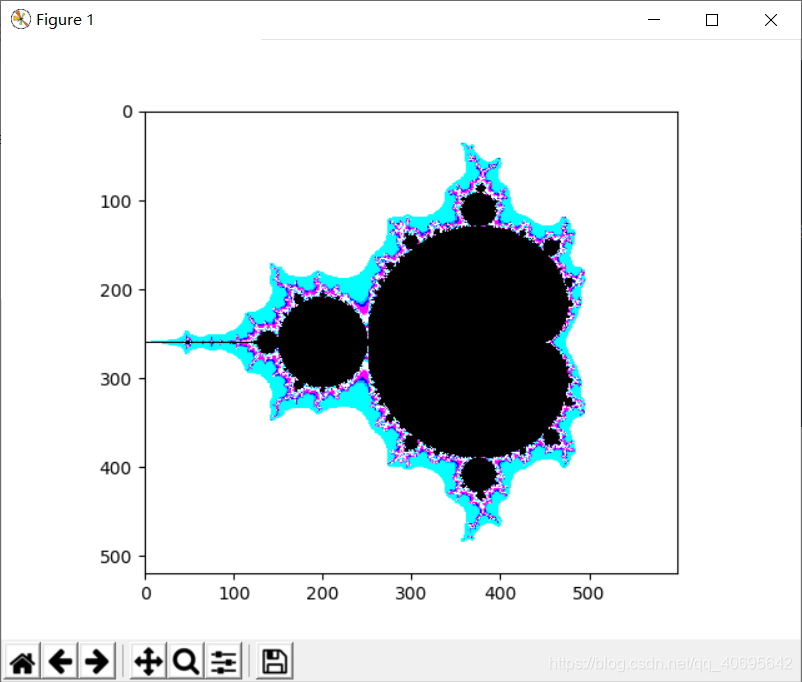
在二维平面上，将所有不属于Mandelbrot集合的点标记为黑色，将所有属于Mandelbrot集合的点按照其发散速度赋予不同的颜色，就可以得到Mandelbrot的经典图像：

请注意: Mandelbrot集合是在$z_0=0$时，不断的迭代c得到。

在生成的Mandelbrot集合中，我们可以将图像放大，选取某些区域进行生成，就可以得到格式各样造型迥异的分形图案。在Mandelbrot集合中，有很多地方图案比较奇特，如下图中的3个位置。

其中编号为2的地方被称为“Elephant Valley”，因为此处的图案与大象很像，直接运行可以得到该区域的图像：

 # Elephant Valleyfractal.gen_mandelbrot(fractal.set_data(x_tuple=(.275, .28),y_tuple=(.006, .01)),rgb=(.9, .6, .6)).save("mandelbrot_area.png")

编号为3的地方被称为“Triple Spiral Valley”(三重螺旋)，在mandelbrot_area.py修改一下坐标位置为(ratio调整的是颜色)：

# 三重螺旋
fractal.gen_mandelbrot(fractal.set_data(x_tuple=(-.09, -.086),y_tuple=(.654, .657)),rgb=(.2, .6, .6)).save("mandelbrot_3.png")

就可以得到该处的图案：

最后编号为1的地方被称为“Seahorse Valley”(海马山谷)，对应的坐标为：

 # Seahorse Valley(海马山谷)fractal.gen_mandelbrot(fractal.set_data(x_tuple=(-.75, -.747),y_tuple=(.099, .102)),rgb=(.1, .1, .3)).save("mandelbrot_sea.png")

图像如下，确实和海马有一点神似：

Julia集合

如果英语还行，建议去维基百科读英文 Julia集合

Julia集合和Mandelbrot集合差不多，但这次我们固定c，转而计算发散的z的值。即c是固定的常数(可以任取)，数列变成$z,z^2+c,(z^2+c{)}^2+c$,……。如果该数列发散，对应的z集合就属于Julia集合。我们看看不同的c值下Julia图案的差别：

$c=-0.835-0.2321i$ 时:

$c=0.285-0.01i$ 时:：

$c=-0.8+0.156i$，图案又变得完全不同：

$c=-0.835-0.2321i$，图案又变得完全不同：

$c=0.70176-0.3842i$，图案成为树状：

生成Julia集合的动画

在Julia集合中，每次都对c的值进行微小的改变，并将依次生成图片制作为gif，就可以生成如下所示的动画: 从这里下载观看， 好像不允许上传gif。程序中提供了一个width参数，可以修改它以生成更大尺寸，质量更高的动画图像。

代码实现

代码采用TensorFlow实现， 比较简单，可以从这里下载代码。希望你能点赞，反馈，谢谢！