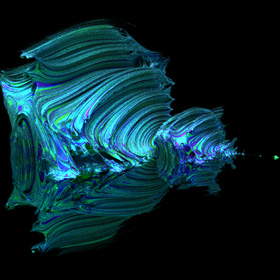
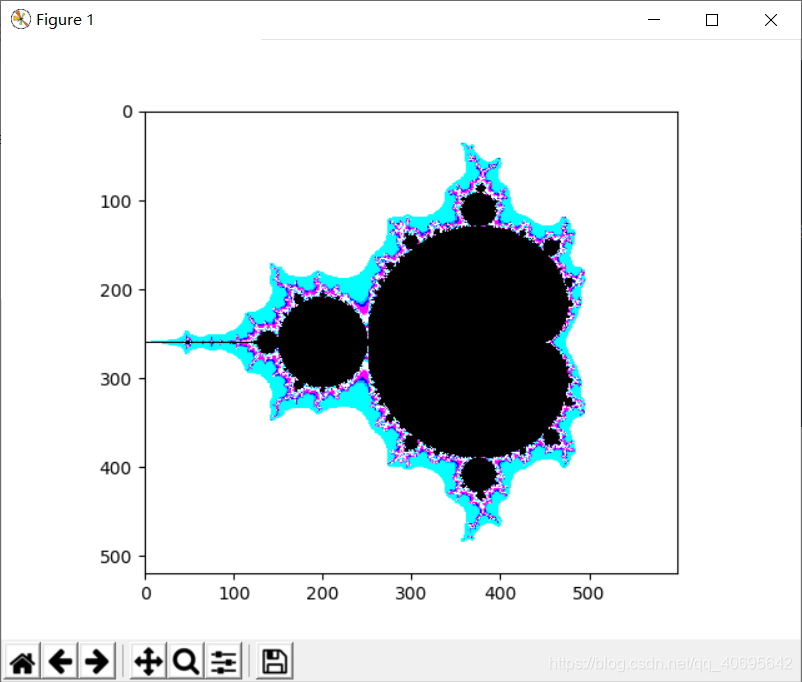
关于 Mandelbrot Set (曼德布洛特集) 的介绍什么的我就不多说了，网上一大堆。唯独清晰的代码不好找，所以我就贴代码吧：

// 需要安装 EasyX 库，Visual C++ 6.0 下编译通过
#include <graphics.h>
#include <conio.h>

/
// 定义复数及乘、加运算
/

// 定义复数
struct COMPLEX
{
    double re;
    double im;
};

// 定义复数“乘”运算
COMPLEX operator * (COMPLEX a, COMPLEX b)
{
    COMPLEX c;
    c.re = a.re * b.re - a.im * b.im;
    c.im = a.im * b.re + a.re * b.im;
    return c;
}

// 定义复数“加”运算
COMPLEX operator + (COMPLEX a, COMPLEX b)
{
    COMPLEX c;
    c.re = a.re + b.re;
    c.im = a.im + b.im;
    return c;
}

/
// 主函数
/
void main()
{
    // 初始化绘图窗口
    initgraph(640, 480);

    /
    // 绘制 Mandelbrot Set (曼德布洛特集)
    /
    COMPLEX z, c;
    for(int x=0; x<640; x++)
    {
        c.re = -2.1 + (1.1 - -2.1) * (x / 640.0);
        for(int y=0; y<480; y++)
        {
            c.im = -1.2 + (1.2 - -1.2) * (y / 480.0);
            z.re = z.im = 0;
            for(int k=0; k<180; k++)
            {
                if ( z.re*z.re + z.im*z.im > 4.0 )    break;
                z = z * z + c;
            }
            putpixel(x, y, (k >= 180) ? 0 : HSLtoRGB((float)((k<<5) % 360), 1.0, 0.5));
        }
    }

    // 按任意键退出
    getch();
    closegraph();
}

效果如图：

为了美观，可以修改一下颜色部分，目前代码中的颜色是这样的：
    HSLtoRGB((float)((k<<5) % 360), 1.0, 0.5)
这行代码中的 k 的取值范围是 0~180，将其映射到 HSL 颜色空间中的色相上(360 度)。