神奇的Python-实现曼德布洛特(Mandelbrot)集合(一行代码，matplotlib numpy，tensorflow)分别实现

Mandelbrot图实际上是由Mandelbrot集合构成的图像。

Mandelbrot集合的定义如下：
$z_{n+1}=z^2_n+c$
其中，c是一个复数。加入给定一个复数 $z_0$ ，比如 $z_0$ =0，那么这个递推式会生成一个序列： $z_0,z_1,z_2,z_3,z_4...]$ 。如果这个序列收敛在一个有限值范围内，那么c就在Mandelbrot集合中。当序列中有一项的绝对值大于2时，这个序列一定趋向于无穷，一般说来，如果这个序列前60项都没有一项大于2，那么可以认为这时c就在Mandelbrot集合中。
在这里插入图片描述

// 一行代码实现曼德布洛特
//原理：Mandelbrot 图像中的每个位置都对应于公式N=x+y*i中的一个复数
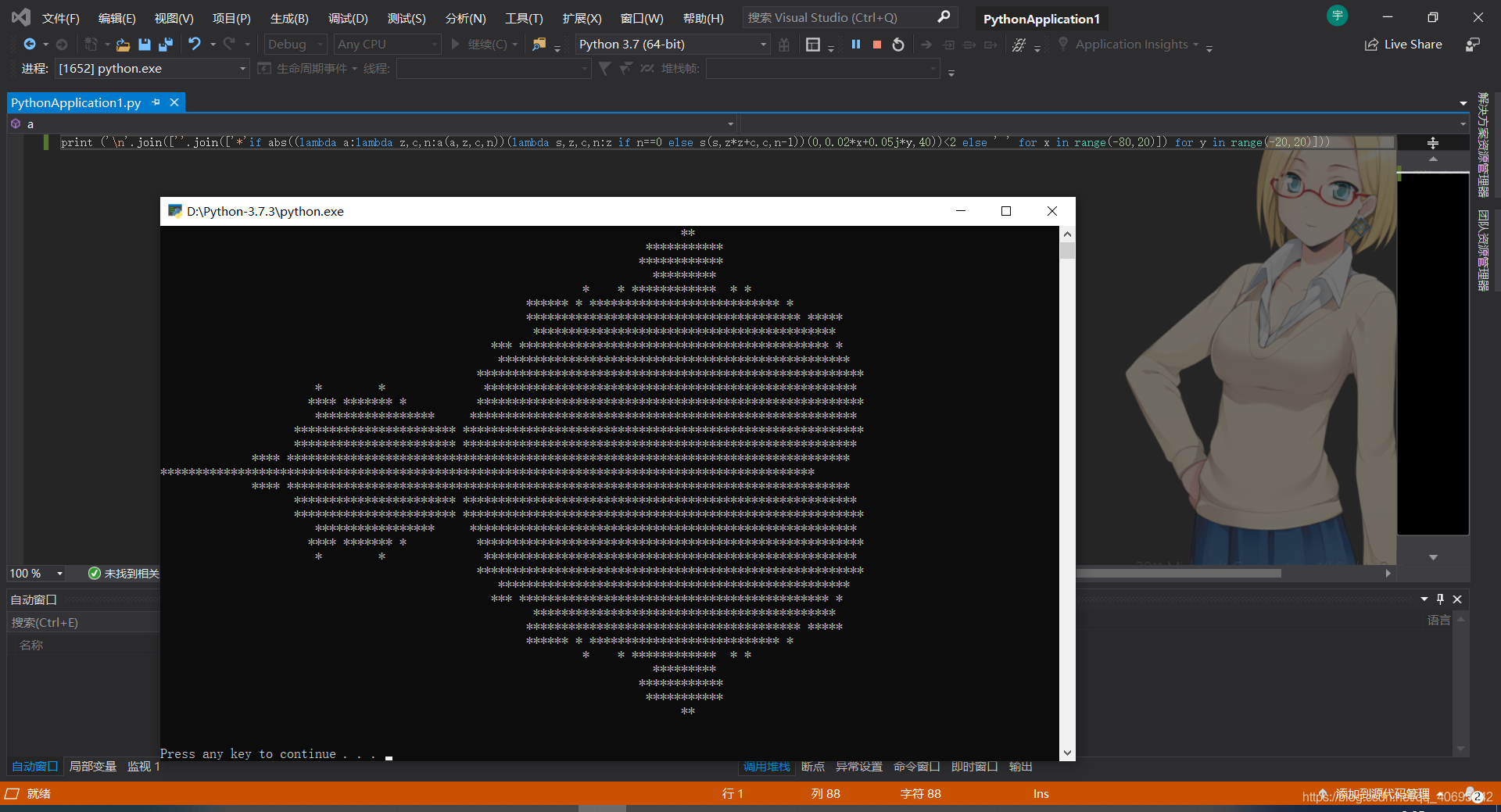
print ('\n'.join([''.join(['*'if abs((lambda a:lambda z,c,n:a(a,z,c,n))(lambda s,z,c,n:z if n==0 else s(s,z*z+c,c,n-1))(0,0.02*x+0.05j*y,40))<2 else ' ' for x in range(-80,20)]) for y in range(-20,20)]))

在这里插入图片描述

//参考以下这位老兄的代码使用matplotlib numpy 曼德尔布罗特集合
// https://blog.csdn.net/DarrenXf/article/details/82563471
import numpy as np
import matplotlib.pyplot as plt 
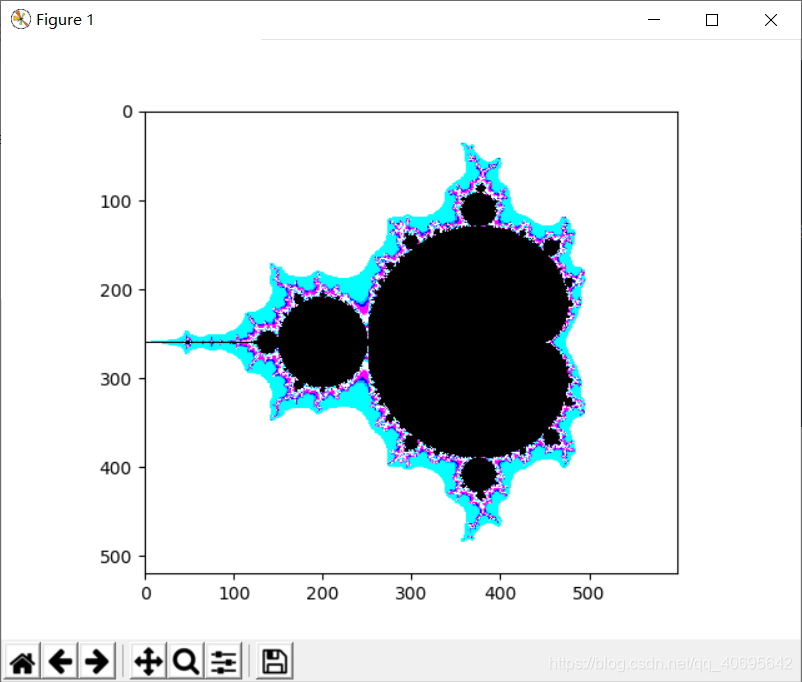
def mandelbrot(h,w,maxit=20):y,x = np.ogrid[-1.4:1.4:h*1j,-2:0.8:w*1j]c = x+y*1jz = c divtime = maxit + np.zeros(z.shape,dtype=int)for i in range(maxit):z = z**2 +cdiverge = z*np.conj(z) > 2**2div_now = diverge & (divtime==maxit)divtime[div_now] = i z[diverge] = 2 return divtimeplt.imshow(mandelbrot(500,500))
plt.show()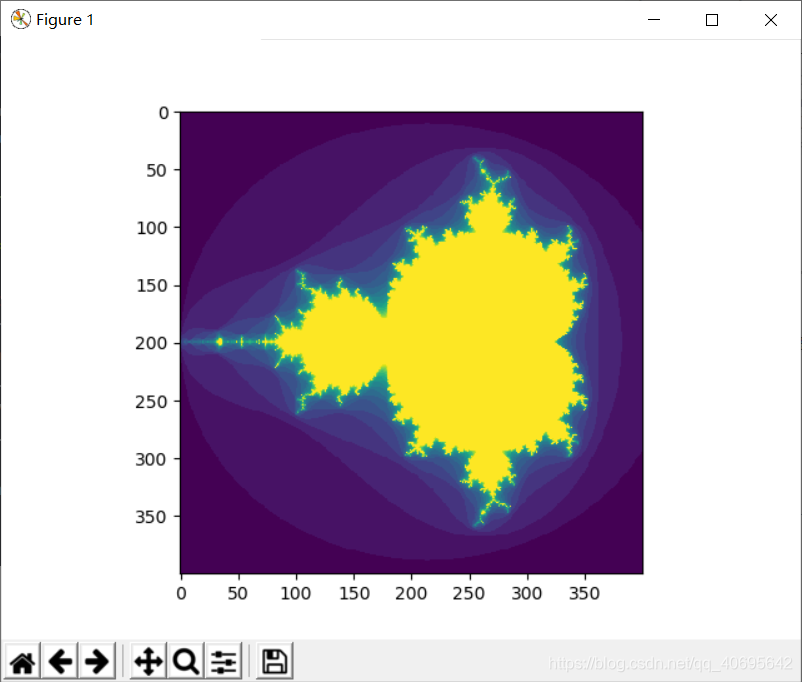

在这里插入图片描述

// 虽然可视化曼德布洛特(Mandelbrot)集合与机器学习没有任何关系，但这对于将TensorFlow应用在数学更广泛的领域是一个有趣的例子。
// 实际上，这是tensorflow一个非常直截了当的可视化运用。
// 原文：TensorFlow社区
// http://www.tensorfly.cn/tfdoc/tutorials/mandelbrot.html
import tensorflow as tf
import numpy as np
#导入可视化
import PIL.Image
// 原文使用from cStringIO import StringIO 这个是python2中的io库
// 在这里我们使用的是python3.7
from io import BytesIO
from IPython.display import Image, display
import matplotlib.pyplot as plt#显示迭代计算出的图像
def DisplayFractal(a, fmt = 'jpeg'):#a_cyclic = (6.28 * a / 20.0).reshape(list(a.shape) + [1])img = np.concatenate([10 + 20 * np.cos(a_cyclic),30 + 50 * np.sin(a_cyclic),155 - 80 * np.cos(a_cyclic)], 2)img[a == a.max()] = 0a = imga = np.uint8(np.clip(a, 0, 255))f = BytesIO()PIL.Image.fromarray(a).save(f, fmt)plt.imshow(img)plt.show()sess = tf.InteractiveSession()#使用Numpy创建一个在[-2,2]x[-2,2]范围内的2维复数数组
Y,X = np.mgrid[-1.3 : 1.3 : 0.005, -2:1:0.005]
Z = X + 1j*Y#定义张量
xs = tf.constant(Z.astype(np.complex64))
zs = tf.Variable(xs)
ns = tf.Variable(tf.zeros_like(xs, tf.float32))tf.global_variables_initializer().run()#计算一个新值z : z^2 + x
zs_ = zs * zs + xs#这个新值会发散么?
not_diverged = tf.abs(zs_) < 4#更新zs并且迭代计算。
#说明：在这些值发散之后，我们仍然在计算zs，这个计算消耗特别大！
#如果稍微简单点，这里有更好的方法来处理。
step = tf.group(
zs.assign(zs_),
ns.assign_add(tf.cast(not_diverged, tf.float32))
)for i in range(200): step.run()DisplayFractal(ns.eval())