Mandelbrot集Julia集分形的MATLAB实现（分形艺术）

1 简单Julia集的实现
- 1.1 如何实现更光滑的展示效果？
2 Mandelbrot集的实现
3 永恒的细节

本文首发于 matlab爱好者微信公众号，欢迎关注。

惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。

本文为学习非线性动力学时，搜索资料时发现的一个小例子，感觉很有趣，试着自己尝试一下。相关实现案例非常多，所以这篇文章就简单水一下了。
其余两篇水文链接也一并奉上：
利用matlab进行混沌摆仿真（双摆、三摆、多摆演示）https://blog.csdn.net/weixin_42943114/article/details/121891553
利用matlab实现复数域空间牛顿迭代法的分形图案展示（newton法）https://blog.csdn.net/weixin_42943114/article/details/121905957

参考目录：
[1]GPU Code Generation: The Mandelbrot Set（https://www.mathworks.com/help/gpucoder/gs/gpu-code-generation-the-mandelbrot-set.html）
[2]神奇的分形艺术（四）：Julia集和Mandelbrot集（http://www.matrix67.com/blog/archives/292）

1 简单Julia集的实现

对于复平面上某个点z，经过函数z=f(z)的不断迭代，会有两种结局：收敛或发散。

当我们取函数f(z)=z^2+C，对整个平面每个点，都经过上述多次迭代后，记录其收敛或发散的情况，并标记在图上，最终形成的图案就是Julia集。C不一定是实数，也可以是复数。

这里我用matlab简单写了一个当C=0.279的图像：
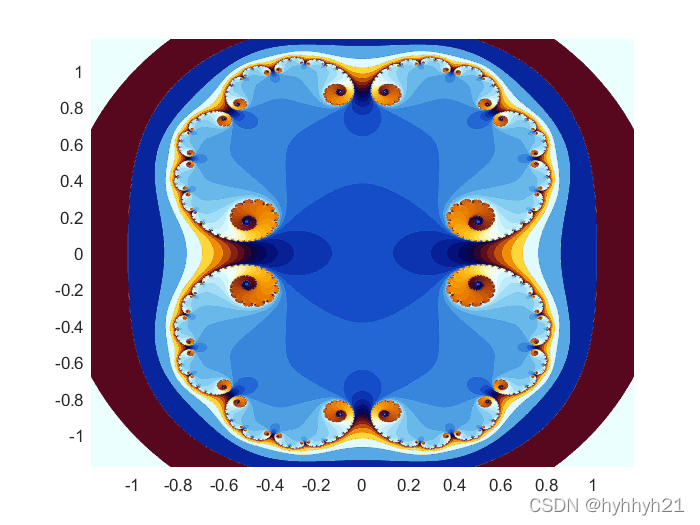
请添加图片描述
这里的颜色条我借鉴的是Matrix67博客里引用的一个图片的颜色条，自己搭配的，见神奇的分形艺术（四）：Julia集和Mandelbrot集。

程序算法参见matlab官方的一个介绍gpu加速的文章中GPU Code Generation: The Mandelbrot Set提到的一种算法。

程序如下：

%?res是目标分辨率，iter是循环次数，（xc,yc）是图像中心，xoom是放大倍数
%res分辨率越多，在一张图上能够计算的点越多。iter越多，细节越丰富。
clear;
clc
close all
res=2500;iter=200;xc=0;yc=0;xoom=1.7;x0=xc-2/xoom;x1=xc+2/xoom;
y0=yc-2/xoom;y1=yc+2/xoom;
x=linspace(x0,x1,res);
y=linspace(y0,y1,res);
[xx,yy]=meshgrid(x,y);
z=xx+yy*1i;C=0.279;
tic%matlab官方推荐的方法
N = ones(res,res);
for k = 0:iterz = z.*z + C;inside = abs( z )<=2;N = N + inside;
end
toc%这里代码参见博客：
%利用matlab构建自己的colormap（色彩搭配）
%https://blog.csdn.net/weixin_42943114/article/details/81811556
%蓝色-橘色颜色条
mycolorpoint=[[235 255 255];...[243 253 242];...[248 247 193];...[255 211 49];...[236 133 0];...[134 36 21];...[75 6 34];...[15 5 64];...[3 8 96];...[7 35 154];...[24 84 205];...[87 169 229];...[165 223 247];...[235 255 255];...];
mycolorposition=[1 3 7 14 27 45 57 66 74 86 96 109 119 128];
mycolormap_r=interp1(mycolorposition,mycolorpoint(:,1),1:128,'pchip','extrap');
mycolormap_g=interp1(mycolorposition,mycolorpoint(:,2),1:128,'pchip','extrap');
mycolormap_b=interp1(mycolorposition,mycolorpoint(:,3),1:128,'pchip','extrap');
mycolor=[mycolormap_r',mycolormap_g',mycolormap_b']/255;figure()
pcolor(x,y,log(N));
mycolor=interp1(linspace(1,256,128),mycolor,1:256);
colormap([mycolor;mycolor;mycolor])%重复颜色条
shading interp

1.1 如何实现更光滑的展示效果？

我在网上查阅资料，发现大部分资料就到此为止了。虽然输出的图片的确像回事，但是它是一个台阶一个台阶的，距离想象中的光滑过度变化有很大差别。
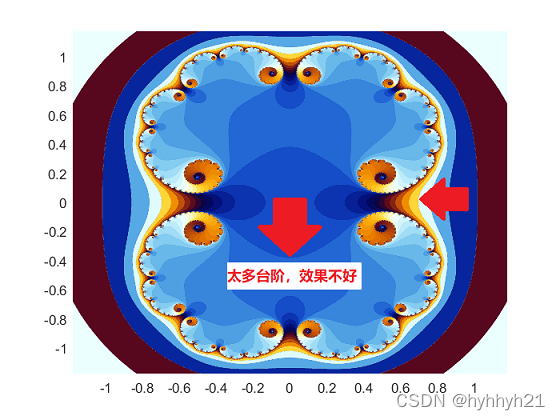
请添加图片描述
这个台阶产生的原因是算法本身，算法用整数去衡量该点发散的快与慢。因此只要算法不更改，整数导致的台阶问题无法消除。所以只能从其他角度去消除这个台阶。

因此我这一小节也提出了一个小改进算法，能够二次加工分形图，去除台阶。之前用过各种滤波法，但是效果不好，因为分形图具有特别多的细节，直接滤波会导致分形图的细节全部丢失。所以后来采用了提取等值线边缘提取的思路，来保持图像形状，再进行光滑插值的方法。效果如下：
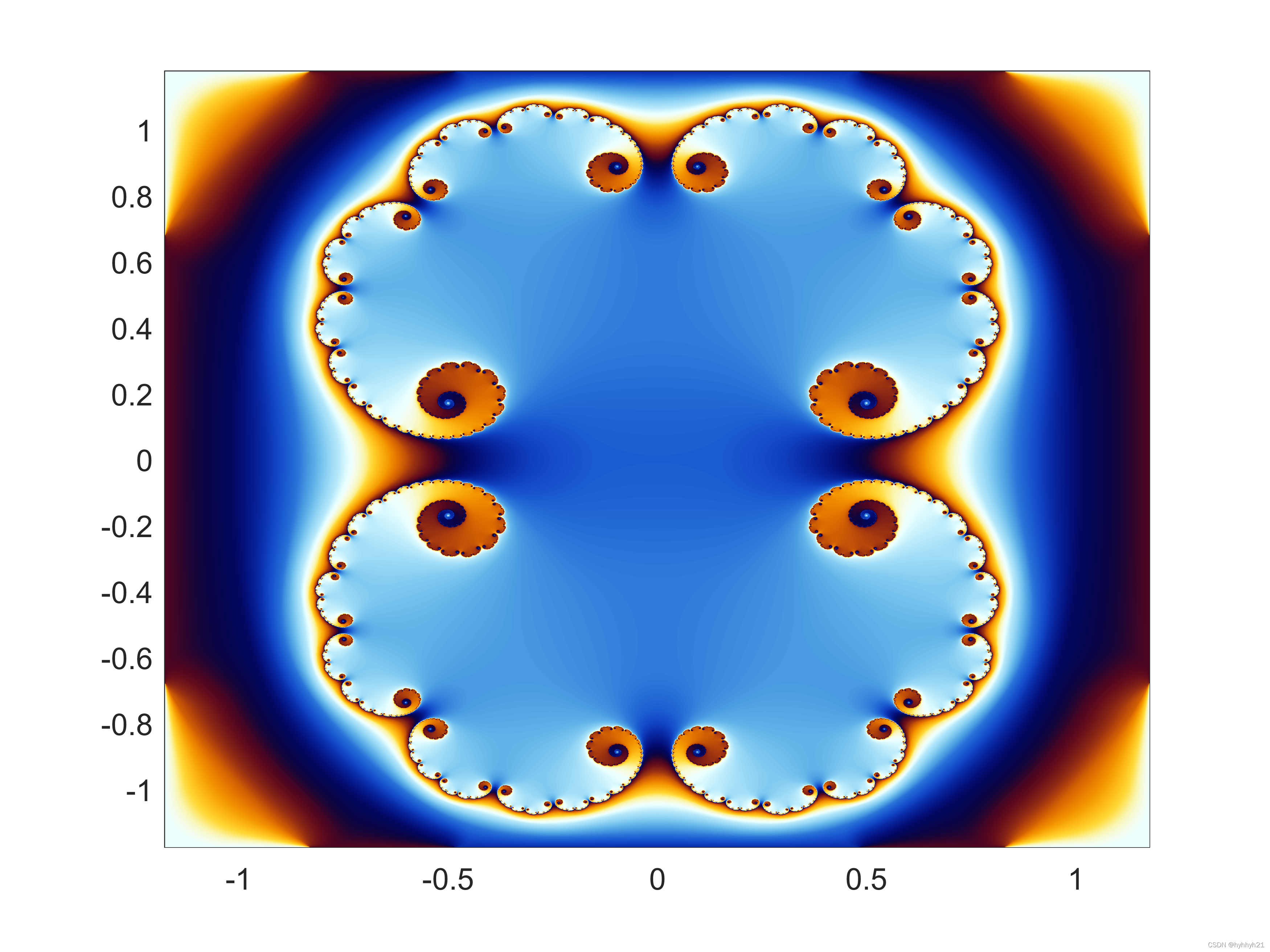
请添加图片描述

可以看到基本保留了大部分分形细节，而且过渡也比较光滑。边缘部分受插值信息限制，可能过渡受边框影响，有些不自然。当然缺点也比较明显，就是我这个轮廓选择原则是逐个像素4个边来决定的，所以计算量非常大。因为之前试过M = contour()函数提取等高线，效果似乎差不多，喜欢折腾的可以在这里再研究一下，看看像Ultra Fractal 之类的分形软件是怎么实现这种效果的。

完整代码如下：

%?res是目标分辨率，iter是循环次数，（xc,yc）是图像中心，xoom是放大倍数
%res分辨率越多，在一张图上能够计算的点越多。iter越多，细节越丰富。
clear;
clc
close all
res=2500;iter=200;xc=0;yc=0;xoom=1.7;x0=xc-2/xoom;x1=xc+2/xoom;
y0=yc-2/xoom;y1=yc+2/xoom;
x=linspace(x0,x1,res);
y=linspace(y0,y1,res);
[xx,yy]=meshgrid(x,y);
z=xx+yy*1i;
C=0.279;
tic%matlab官方推荐
N = ones(res,res);
for k = 0:iterz = z.*z + C;inside = abs( z )<=2;N = N + inside;
end
tocmycolorpoint=[[235 255 255];[243 253 242];[248 247 193];[255 211 49];...[236 133 0];[134 36 21];[75 6 34];[15 5 64];...[3 8 96];[7 35 154];[24 84 205];[87 169 229];...[165 223 247];[235 255 255]; ];
mycolorposition=[1 3 7 14 27 45 57 66 74 86 96 109 119 128];
mycolormap_r=interp1(mycolorposition,mycolorpoint(:,1),1:128,'pchip','extrap');
mycolormap_g=interp1(mycolorposition,mycolorpoint(:,2),1:128,'pchip','extrap');
mycolormap_b=interp1(mycolorposition,mycolorpoint(:,3),1:128,'pchip','extrap');
mycolor=[mycolormap_r',mycolormap_g',mycolormap_b']/255;%输出
figure()
pcolor(x,y,log(N));
mycolor=interp1(linspace(1,256,128),mycolor,1:256);
colormap([mycolor;mycolor;mycolor])
shading interp%二次光滑
Nq=LowPrecision2High(N);
figure()
pcolor(x,y,log(Nq));
colormap([mycolor;mycolor;mycolor])
shading interpfunction Zq=LowPrecision2High(Z)
%对阶梯数据进行平滑
[Nx,Ny]=size(Z);
[X,Y]=meshgrid(1:Nx,1:Ny);
XP=[];YP=[];ZP=[];
for kx=1:(Nx-1)for ky=1:(Ny-1)if Z(kx,ky)~=Z(kx,ky+1)x_t=0.5*(X(kx,ky)+X(kx,ky+1));y_t=0.5*(Y(kx,ky)+Y(kx,ky+1));z_t=0.5*(Z(kx,ky)+Z(kx,ky+1));XP=[XP;x_t];YP=[YP;y_t];ZP=[ZP;z_t];endif Z(kx,ky)~=Z(kx+1,ky)x_t=0.5*(X(kx,ky)+X(kx+1,ky));y_t=0.5*(Y(kx,ky)+Y(kx+1,ky));z_t=0.5*(Z(kx,ky)+Z(kx+1,ky));XP=[XP;x_t];YP=[YP;y_t];ZP=[ZP;z_t];endend
end
%边界值
for kx=1:NxXP=[XP;X(kx,1)];  YP=[YP;Y(kx,1)];  ZP=[ZP;Z(kx,1)];XP=[XP;X(kx,end)];YP=[YP;Y(kx,end)];ZP=[ZP;Z(kx,end)];
end
for ky=2:Ny-1XP=[XP;X(1,ky)];  YP=[YP;Y(1,ky)];  ZP=[ZP;Z(1,ky)];XP=[XP;X(end,ky)];YP=[YP;Y(end,ky)];ZP=[ZP;Z(end,ky)];
end
Zq=griddata(XP,YP,ZP,X,Y,'natural');%'v4'最好，但是速度最慢。实在不行用linear，快一点但不好看。
end

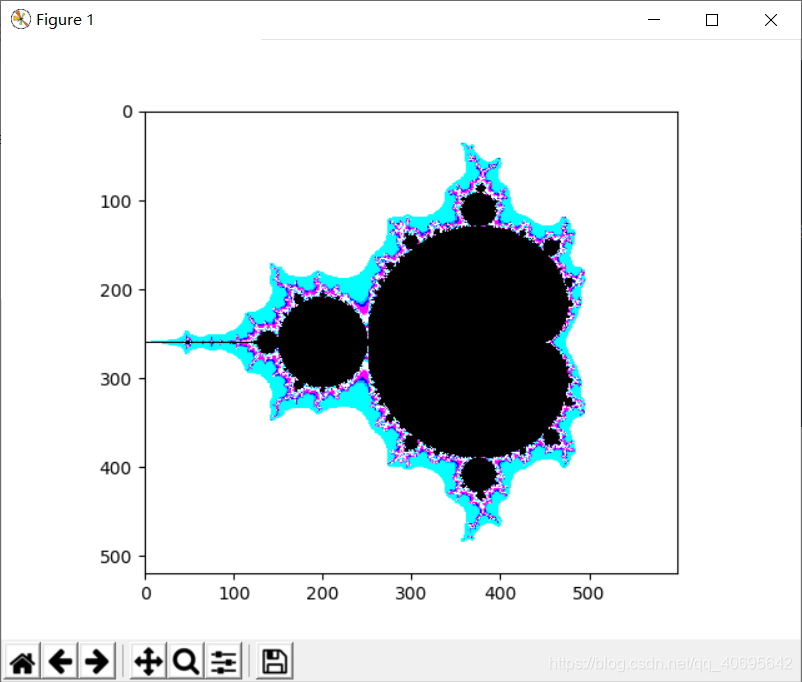
2 Mandelbrot集的实现

Mandelbrot集的求解方法和Julia集类似，就是方程不一样，它不再是常数C，而是把C替换成了z0。
$f(z)=z^2+z_0$
这里z0代表初始迭代的点坐标。
结果如下：
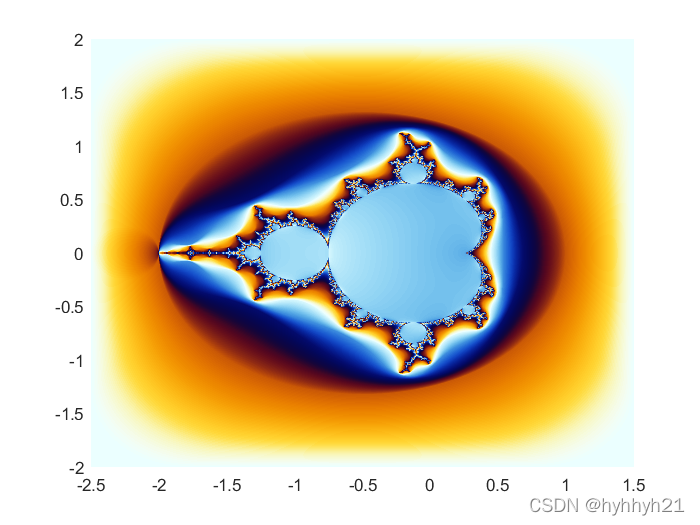
请添加图片描述
代码如下：

%?res是目标分辨率，iter是循环次数，（xc,yc）是图像中心，xoom是放大倍数
%res分辨率越多，在一张图上能够计算的点越多。iter越多，细节越丰富。
clear;
clc
close all
res=1024;iter=100;xc=-0.5;yc=0;xoom=1;%这个可以自己调试，用来观察细节x0=xc-2/xoom;x1=xc+2/xoom;
y0=yc-2/xoom;y1=yc+2/xoom;
x=linspace(x0,x1,res);
y=linspace(y0,y1,res);
[xx,yy]=meshgrid(x,y);
z=xx+yy*1i;
C=z;
tic%matlab官方推荐
N = ones(res,res);
for k = 0:iterz = z.*z + C;inside = abs( z )<=2;N = N + inside;
end
tocmycolorpoint=[[235 255 255];[243 253 242];[248 247 193];[255 211 49];...[236 133 0];[134 36 21];[75 6 34];[15 5 64];...[3 8 96];[7 35 154];[24 84 205];[87 169 229];...[165 223 247];[235 255 255]; ];
mycolorposition=[1 3 7 14 27 45 57 66 74 86 96 109 119 128];
mycolormap_r=interp1(mycolorposition,mycolorpoint(:,1),1:128,'pchip','extrap');
mycolormap_g=interp1(mycolorposition,mycolorpoint(:,2),1:128,'pchip','extrap');
mycolormap_b=interp1(mycolorposition,mycolorpoint(:,3),1:128,'pchip','extrap');
mycolor=[mycolormap_r',mycolormap_g',mycolormap_b']/255;%输出
figure()
pcolor(x,y,log(N));
mycolor=interp1(linspace(1,256,128),mycolor,1:256);
colormap([mycolor;mycolor;mycolor])
shading interp%二次光滑
Nq=LowPrecision2High(N);
figure()
pcolor(x,y,log(Nq));
colormap([mycolor;mycolor;mycolor])
shading interpfunction Zq=LowPrecision2High(Z)
%对阶梯数据进行平滑
[Nx,Ny]=size(Z);
[X,Y]=meshgrid(1:Nx,1:Ny);
XP=[];YP=[];ZP=[];
for kx=1:(Nx-1)for ky=1:(Ny-1)if Z(kx,ky)~=Z(kx,ky+1)x_t=0.5*(X(kx,ky)+X(kx,ky+1));y_t=0.5*(Y(kx,ky)+Y(kx,ky+1));z_t=0.5*(Z(kx,ky)+Z(kx,ky+1));XP=[XP;x_t];YP=[YP;y_t];ZP=[ZP;z_t];endif Z(kx,ky)~=Z(kx+1,ky)x_t=0.5*(X(kx,ky)+X(kx+1,ky));y_t=0.5*(Y(kx,ky)+Y(kx+1,ky));z_t=0.5*(Z(kx,ky)+Z(kx+1,ky));XP=[XP;x_t];YP=[YP;y_t];ZP=[ZP;z_t];endend
end
%边界值
for kx=1:NxXP=[XP;X(kx,1)];  YP=[YP;Y(kx,1)];  ZP=[ZP;Z(kx,1)];XP=[XP;X(kx,end)];YP=[YP;Y(kx,end)];ZP=[ZP;Z(kx,end)];
end
for ky=2:Ny-1XP=[XP;X(1,ky)];  YP=[YP;Y(1,ky)];  ZP=[ZP;Z(1,ky)];XP=[XP;X(end,ky)];YP=[YP;Y(end,ky)];ZP=[ZP;Z(end,ky)];
end
Zq=griddata(XP,YP,ZP,X,Y,'natural');%'v4'最好，但是速度最慢。实在不行用linear，快一点但不好看。
end

3 永恒的细节

分形图案最有意思的，在于其看似有规律却又不可描述的图像，以及无穷无尽直至永恒的细节。

我们以Mandelbort集为例，在上一节的程序里，只需要变动xc=-0.5;yc=0;xoom=1;这几个数，便可以改变镜头的中心位置和放大倍数。
现在将(-0.912,-0.2611)这一点放大，可以得到：
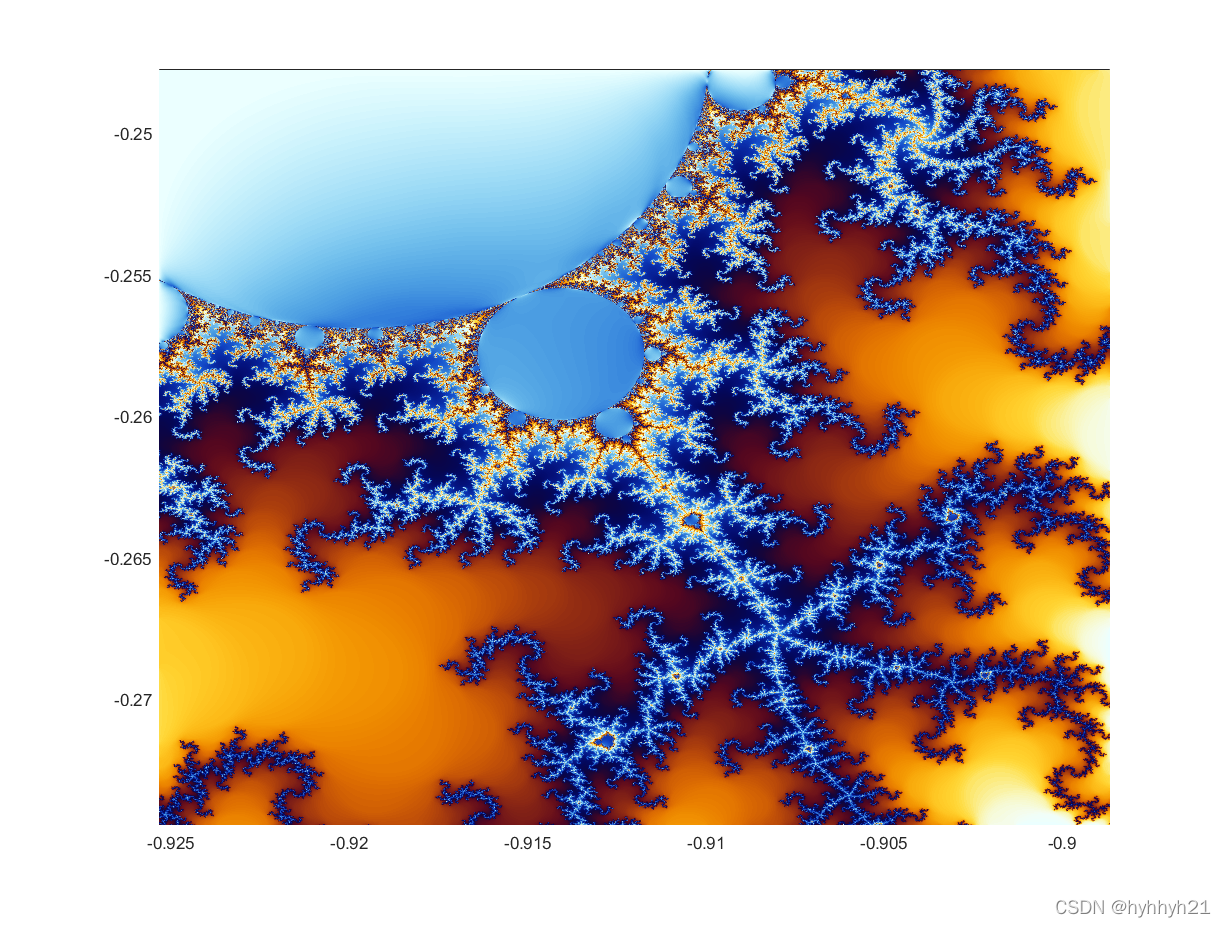
请添加图片描述
可以看到放大图像之后，细节并没有减少，反而更多的细节被展示出来，跳到面前，用精巧的结构引诱人们进一步的放大图像。它的图像最有规律，每一处都透露着美感；它的图像又毫无规律，无法用现有的数学语言去描述。它的方程非常简单，但它产生的结构又非常复杂。

最后用一个动图来展示其魅力（扫兴的是gif图片上传有大小限制，所以只能压缩到渣画质，分割为两个图上传了，非常道歉）

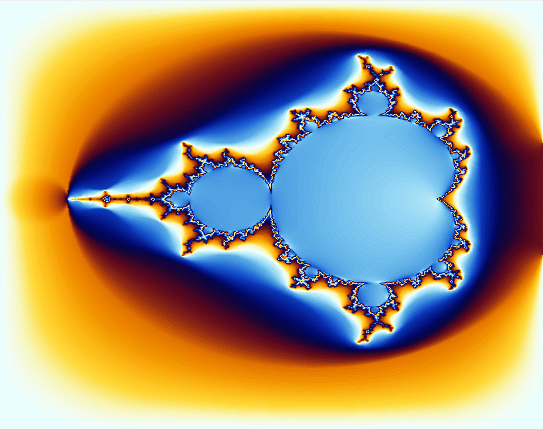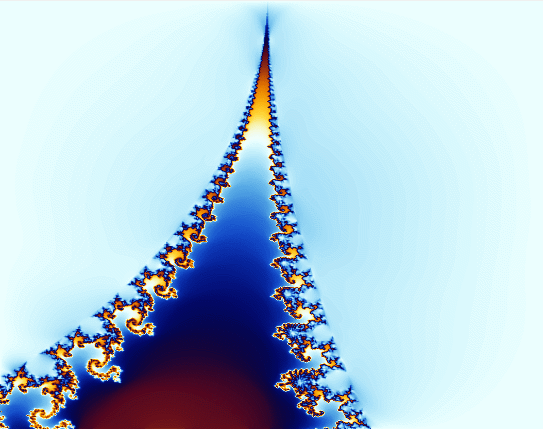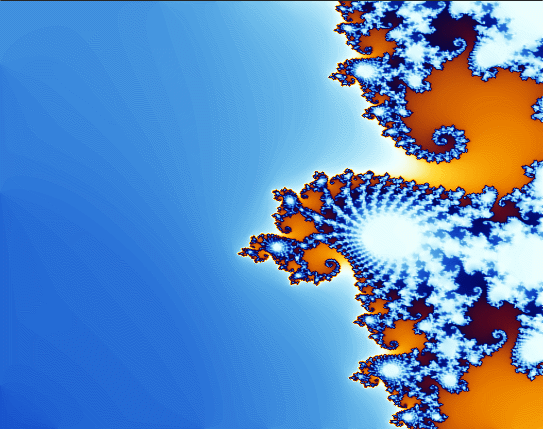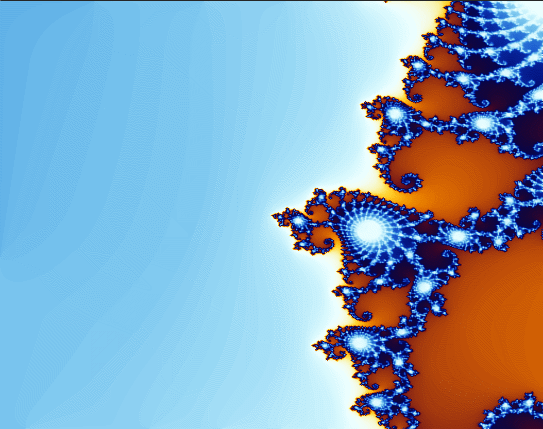
请添加图片描述
。

第二个图，接上一个：
。
请添加图片描述
下面放代码：

↓

%Mandelbrot
%http://www.matrix67.com/blog/archives/292
%?res是目标分辨率，iter是循环次数，（xc,yc）是图像中心，xoom是放大倍数
clear;
res=512;iter=200;xc=-0.748766710846959;yc=-0.123640847970064;mycolorpoint=[[235 255 255];[243 253 242];[248 247 193];[255 211 49];...[236 133 0];[134 36 21];[75 6 34];[15 5 64];...[3 8 96];[7 35 154];[24 84 205];[87 169 229];...[165 223 247];[235 255 255]; ];
mycolorposition=[1 3 7 14 27 45 57 66 74 86 96 109 119 128];
mycolormap_r=interp1(mycolorposition,mycolorpoint(:,1),1:128,'pchip','extrap');
mycolormap_g=interp1(mycolorposition,mycolorpoint(:,2),1:128,'pchip','extrap');
mycolormap_b=interp1(mycolorposition,mycolorpoint(:,3),1:128,'pchip','extrap');
mycolor=[mycolormap_r',mycolormap_g',mycolormap_b']/255;
mycolor=interp1(linspace(1,256,128),mycolor,1:256);
colormap([mycolor;mycolor;mycolor])GIF=2;%第二段动画
for m=(1+46*GIF):46*(GIF+1)xoom=1.2^m;%xoom=6.503637847981780e+08;x0=xc-2/xoom;x1=xc+2/xoom;y0=yc-2/xoom;y1=yc+2/xoom;x=linspace(x0,x1,res);y=linspace(y0,y1,res);[xx,yy]=meshgrid(x,y);z=xx+yy*1i;C=z;%matlab官方推荐N = ones(res,res);for k = 0:iterz = z.*z + C;inside = abs( z )<=2;N = N + inside;endNq=LowPrecision2High(N);figure(1)clfpcolor(x,y,log(Nq));shading interpcolormap([mycolor;mycolor;mycolor])caxis([0,log(iter+2)])%生成gif图pause(0.1)F=getframe(gca);I=frame2im(F);[I,map]=rgb2ind(I,256);if m == (1+46*GIF)imwrite(I,map,'test.gif','gif','Loopcount',inf,'DelayTime',0.2);elseimwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.2);end
endfunction Zq=LowPrecision2High(Z)
[Nx,Ny]=size(Z);
[X,Y]=meshgrid(1:Nx,1:Ny);
XP=[];YP=[];ZP=[];
for kx=1:(Nx-1)for ky=1:(Ny-1)if Z(kx,ky)~=Z(kx,ky+1)x_t=0.5*(X(kx,ky)+X(kx,ky+1));y_t=0.5*(Y(kx,ky)+Y(kx,ky+1));z_t=0.5*(Z(kx,ky)+Z(kx,ky+1));XP=[XP;x_t];YP=[YP;y_t];ZP=[ZP;z_t];endif Z(kx,ky)~=Z(kx+1,ky)x_t=0.5*(X(kx,ky)+X(kx+1,ky));y_t=0.5*(Y(kx,ky)+Y(kx+1,ky));z_t=0.5*(Z(kx,ky)+Z(kx+1,ky));XP=[XP;x_t];YP=[YP;y_t];ZP=[ZP;z_t];%pause(0.1)endend
end
%边界值
for kx=1:NxXP=[XP;X(kx,1)];  YP=[YP;Y(kx,1)];  ZP=[ZP;Z(kx,1)];XP=[XP;X(kx,end)];YP=[YP;Y(kx,end)];ZP=[ZP;Z(kx,end)];
end
for ky=2:Ny-1XP=[XP;X(1,ky)];  YP=[YP;Y(1,ky)];  ZP=[ZP;Z(1,ky)];XP=[XP;X(end,ky)];YP=[YP;Y(end,ky)];ZP=[ZP;Z(end,ky)];
end
Zq=griddata(XP,YP,ZP,X,Y,'natural');%'v4'最好，实在不行用linear
end