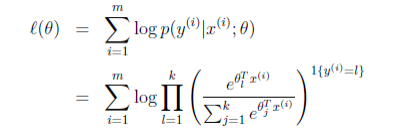广义线性模型2

article/2025/8/19 16:05:19

1.1.2 Ridge Regression[岭回归]

岭回归和普通最小二乘法回归的一个重要区别是前者对系数模的平方进行了限制。如下所示：

In [1]: from sklearn import linear_modelIn [2]: clf = linear_model.R
linear_model.RandomizedLasso
linear_model.RandomizedLogisticRegression
linear_model.Ridge
linear_model.RidgeCV
linear_model.RidgeClassifier
linear_model.RidgeClassifierCVIn [2]: clf = linear_model.Ridge(alpha = .5)In [3]: clf.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Out[3]: 
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,normalize=False, solver='auto', tol=0.001)In [4]: clf.coef_
Out[4]: array([ 0.34545455,  0.34545455])In [5]: clf.intercept_
Out[5]: 0.13636363636363641

解析：

[1]sklearn.linear_model.Ridge类构造方法

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto')

[2]sklearn.linear_model.Ridge类实例的属性和方法

[3]Ridge Regression[岭回归]

岭回归分析是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的耐受性远远强于最小二乘法。岭回归分析主要解决两类问题：数据点少于变量个数；变量间存在共线性。

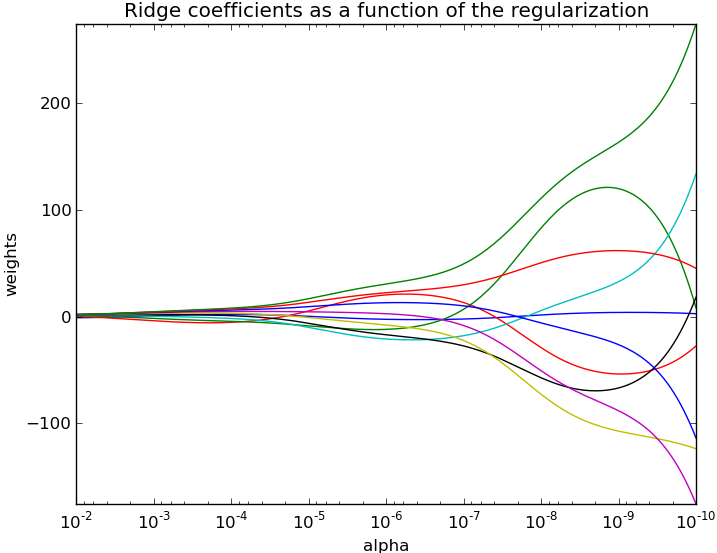
Examples: Plot Ridge coefficients as a function of the regularization

print(__doc__)import numpy as np
import pylab as pl
from sklearn import linear_model# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)###############################################################################
# Compute pathsn_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
clf = linear_model.Ridge(fit_intercept=False)coefs = []
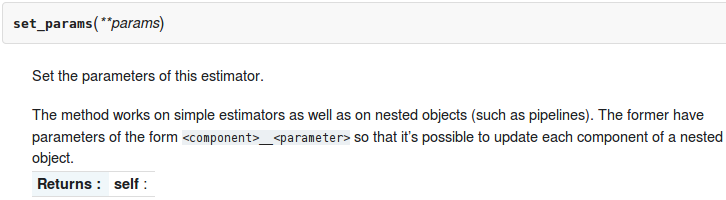
for a in alphas:clf.set_params(alpha=a)clf.fit(X, y)coefs.append(clf.coef_)###############################################################################
# Display resultsax = pl.gca()
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
pl.xlabel('alpha')
pl.ylabel('weights')
pl.title('Ridge coefficients as a function of the regularization')
pl.axis('tight')
pl.show()

图形输出，如下所示：

解析：

[1]希尔伯特矩阵

在线性代数中，希尔伯特矩阵是一种系数都是单位分数的方块矩阵。

[2]np.arange()方法

In [31]: 1. / (np.arange(1, 11))
Out[31]: 
array([ 1.        ,  0.5       ,  0.33333333,  0.25      ,  0.2       ,0.16666667,  0.14285714,  0.125     ,  0.11111111,  0.1       ])In [32]: (1. / (np.arange(1, 11))).shape
Out[32]: (10,)

[3]np.newaxis属性

In [5]: np.arange(0, 10)
Out[5]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])In [6]: type(np.arange(0, 10))
Out[6]: numpy.ndarrayIn [7]: np.arange(0, 10).shape
Out[7]: (10,)In [8]: np.arange(0, 10)[:, np.newaxis]
Out[8]: 
array([[0],[1],[2],[3],[4],[5],[6],[7],[8],[9]])In [9]: np.arange(0, 10)[:, np.newaxis].shape
Out[9]: (10, 1)

[4]广播原理

In [25]: x = np.arange(0, 5)In [26]: x[:, np.newaxis]
Out[26]: 
array([[0],[1],[2],[3],[4]])In [27]: x[np.newaxis, :]
Out[27]: array([[0, 1, 2, 3, 4]])In [28]: x[:, np.newaxis] + x[np.newaxis, :]
Out[28]: 
array([[0, 1, 2, 3, 4],[1, 2, 3, 4, 5],[2, 3, 4, 5, 6],[3, 4, 5, 6, 7],[4, 5, 6, 7, 8]])

[5]10阶希尔伯特矩阵X

In [33]: X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])In [34]: X
Out[34]: 
array([[ 1.        ,  0.5       ,  0.33333333,  0.25      ,  0.2       ,0.16666667,  0.14285714,  0.125     ,  0.11111111,  0.1       ],[ 0.5       ,  0.33333333,  0.25      ,  0.2       ,  0.16666667,0.14285714,  0.125     ,  0.11111111,  0.1       ,  0.09090909],[ 0.33333333,  0.25      ,  0.2       ,  0.16666667,  0.14285714,0.125     ,  0.11111111,  0.1       ,  0.09090909,  0.08333333],[ 0.25      ,  0.2       ,  0.16666667,  0.14285714,  0.125     ,0.11111111,  0.1       ,  0.09090909,  0.08333333,  0.07692308],[ 0.2       ,  0.16666667,  0.14285714,  0.125     ,  0.11111111,0.1       ,  0.09090909,  0.08333333,  0.07692308,  0.07142857],[ 0.16666667,  0.14285714,  0.125     ,  0.11111111,  0.1       ,0.09090909,  0.08333333,  0.07692308,  0.07142857,  0.06666667],[ 0.14285714,  0.125     ,  0.11111111,  0.1       ,  0.09090909,0.08333333,  0.07692308,  0.07142857,  0.06666667,  0.0625    ],[ 0.125     ,  0.11111111,  0.1       ,  0.09090909,  0.08333333,0.07692308,  0.07142857,  0.06666667,  0.0625    ,  0.05882353],[ 0.11111111,  0.1       ,  0.09090909,  0.08333333,  0.07692308,0.07142857,  0.06666667,  0.0625    ,  0.05882353,  0.05555556],[ 0.1       ,  0.09090909,  0.08333333,  0.07692308,  0.07142857,0.06666667,  0.0625    ,  0.05882353,  0.05555556,  0.05263158]])

[6]np.ones()方法

In [35]: y = np.ones(10)In [36]: y
Out[36]: array([ 1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.])In [37]: y.shape
Out[37]: (10,)

[7]numpy.logspace()方法

numpy.logspace(start, stop, num=50, endpoint=True, base=10.0)

说明：Return numbers spaced evenly on a log scale. In linear space, the sequence starts at base ** start (base to the power of start) and ends with base ** stop (see endpoint below).

In [38]: n_alphas = 200In [39]: alphas = np.logspace(-10, -2, n_alphas)In [40]: alphas
Out[40]: 
array([  1.00000000e-10,   1.09698580e-10,   1.20337784e-10,1.32008840e-10,   1.44811823e-10,   1.58856513e-10,1.74263339e-10,   1.91164408e-10,   2.09704640e-10,...,5.23109931e-03,   5.73844165e-03,   6.29498899e-03,6.90551352e-03,   7.57525026e-03,   8.30994195e-03,9.11588830e-03,   1.00000000e-02])In [41]: alphas.shape
Out[41]: (200,)In [42]: 1.00000000e-10
Out[42]: 1e-10

[8]set_params(**params)方法

[9]matplotlib.pyplot.gca(**kwargs)方法

Return the current axis instance. This can be used to control axis properties either using set or the Axes methods, for example, setting the x axis range.

参考文献：

[1] 岭回归: http://baike.baidu.com/link?url=S1DwT9XFOthlB5hjGP6Ramxt-fvtCJ-RUXYVSw-z9t7-hZIojL7eroUQwKaJd5KE9-jVEQeRtxZeuUz59SBE6q

[2] 正则化、归一化含义解析: http://sobuhu.com/ml/2012/12/29/normalization-regularization.html

[3] 希尔伯特矩阵: http://zh.wikipedia.org/zh-cn/%E5%B8%8C%E5%B0%94%E4%BC%AF%E7%89%B9%E7%9F%A9%E9%98%B5

[4] 岭回归分析总结: http://download.csdn.net/detail/shengshengwang/7225251