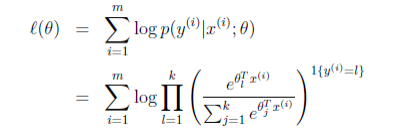第1章 多元统计分析概述
第2章 多元数据的数学表达
第3章 多元数据的直观表示
第4章 多元相关与回归分析
第5章 广义与一般线性模型
- 5.1 模型的选择
- 5.2 广义线性模型
- 5.3 一般线性模型
第6章 判别分析及R使用
第7章 聚类分析及R使用
第8章 主成分分析及R使用
第9章 因子分析及R使用
第10章 对应分析及R使用
第11章 典型相关分析及R使用
第12章 多维标度法及R 使用
第13章 综合评价方法及R使用




——————————————————————
5.2

- 广义线性模型是说y已经不是正太分布,或者已经不是连续的了,他的分布可能是二项分布,泊松分布等。
- 不管是正态分布,二项分布,泊松分布等都是归于指数分布族里

R语言中广义线性模型函数glm()的用法

这里叫logistic模型而不是线性回归模型,因为这里logist(y),而不是y。是做了一个logistic变换。
这个驾驶员出不出事故的例子是个二分类的例子。

library(openxlsx)
#读取例子5.1数据
d5.1 = read.xlsx('mvstats5.xlsx','d5.1')
logit = glm(y~x1+x2+x3, family = binomial, data = d5.1)#logistic模型,family是二项分布
summary(logit)

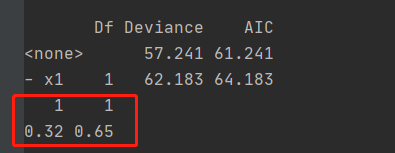
结果如上图,其结果和之前的线性模型类似,但这里不是对整体的结果的一个检验,只是对每个回归系数进行的检验。其中x1有个*,说明x1(视力因素)直接影响到结果,即出不出交通事故。x2和x3基本影响不大。

通过逐步筛选变量就可以把除x1外,其他两个变量就被筛掉了。
python
#逐步筛选变量logistic回归模型
logit.step = step(logit)
summary(logit.step)


#预测视力正常司机logistic回归结果
pre1 = predict(logit.step, data.frame(x1 = 1))
#预测视力正常司机发生事故概率
p1 = exp(pre1)/(1 + exp(pre1))
##预测视力有问题司机logistic回归结果
pre2 = predict(logit.step,data.frame(x1 = 0))
#预测视力有问题司机发生事故概率
p2 = exp(pre2)/(1 + exp(pre2))
c(p1,p2)#结果显示


5.3 一般线性模型

一般线性模型和广义线性模型的区别在于:y仍然是正态分布,但自变量x有可能是分类变量。这类模型如方差分析。




本系列是多元统计分析及R语言建模,是王斌会、侯雅文、徐锋、何志锋、颜斌等老师的慕课课程,对各位老师表示敬意与感谢。课程链接,项目源码和数据集如下:
https://www.icourse163.org/learn/JNU-1002335007?tid=1449765441#/learn/content
https://github.com/idiotprofessorchen/R_multivariate_statistical_analysis