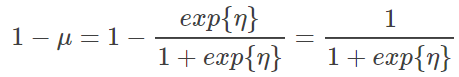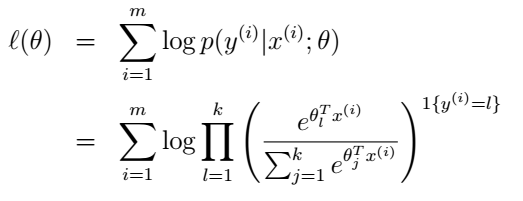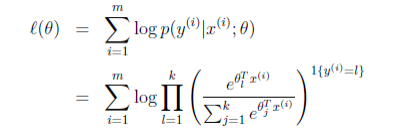广义线性模型

广义线性模型[generalize linear model(GLM)]是线性模型的扩展，通过连接函数建立响应变量的数学期望值与线性组合的预测变量之间的关系。首先从数学上来看，模型即:

1. y|x;$\beta$ ~ Exponential distribution family($\theta$)
2. $g(E[y|x])={\beta }^{\prime }x$, 其中g称为连接函数(link function)

这两点假设是GLM的核心，也即首先因变量y的条件分布(给定自变量X)是服从指数分布族的，其次存在一个连接函数g，能够将我们的预测子$E[y|x]$与线性表达式${\beta }^{\prime }x$之间搭起一个桥梁。因此连接函数也是GLM的一个核心。因此要学习GLM，首先得从指数分布族与连接函数讲起。

指数分布族

指数分布族是一类分布，如果某一分布的概率密度函数可写成以下形式，称其属于指数分布族：
f ( y ) = e x p { y θ − b ( θ ) a ( ϕ ) + c ( y , ϕ ) } f(y) = exp\{\frac{y\theta-b(\theta)}{a(\phi)}+c(y, \phi)\} f(y)=exp{a(ϕ)yθ−b(θ)​+c(y,ϕ)}
其中$\theta$称为自然参数或正则参数，$\varphi$称为尺度参数，a,b,c均为函数。
指数分布族包含了我们熟知的很多分布，基本上概率论与数理统计里面的分布都属于指数分布族，如正态分布，伽马分布，二项分布，泊松分布，负二项分布等。
其实关于指数分布族的表示，通常有两种版本，以上为一种，还有一种为：
f ( y ) = h ( y ) exp ⁡ { η ( θ ) T ( y ) − A ( η ) } f(y)=h(y)\exp \{\eta ({\theta })T(y)-A({\eta })\} f(y)=h(y)exp{η(θ)T(y)−A(η)}
其实这两种表达差不多，可以相互转化，充分统计量T(y)通常就是y，具体转化读者可自行研究。
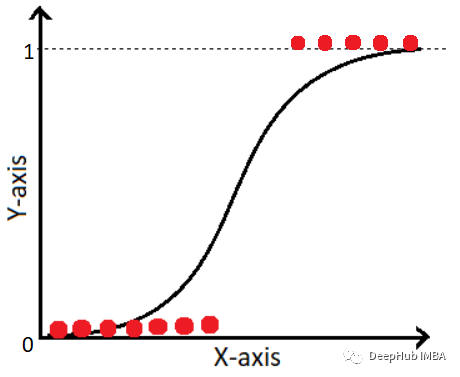
以下举两个栗子，为伯努利分布与正态分布化为指数分布族形式：

关于更多分布转化为指数分布族的细节，可参考Wikipedia指数分布族。

性质

如若将y的概率密度函数写成指数分布族的形式，并且确定了$\theta ,\varphi ,a,b,c$的形式，那么利用这些参数的信息，能够很轻松的求的分布的期望与方差：

• $E(y)=b^{\prime }(\theta )$
• $Var(y)=b^{\prime \prime }(\theta )a(\varphi )$

其中b’和b’'为一阶和二阶导数。以伯努利分布与正态分布举例：

连接函数

前文说过，连接函数即预测子$E[y|x]$与线性表达式${\beta }^{\prime }x$之间的一个桥梁。$E[y|x]$也即y条件分布的参数，因此g是一个将待估参数映射为线性表达式的一个函数，这样就无需直接对参数进行估计，利用连接函数g，转而估计线性表达式中的$\beta$

如果将2写成逆函数的形式，即$E[y|x]=g^{-1}({\beta }^{\prime }x)$，那么连接函数反过来为y的条件分布的参数提供了一种估计办法（当然比较鸡肋…

正则连接函数(canonical link function)

连接函数从形式上看，可以有很多种，毕竟是可以用户自定。因此需要加上一点限制，使得能够使用的连接函数只有一个。
在连接函数的基础之上，对GLM再增加一点假设

• $\theta ={\beta }^{\prime }x$，$\theta$为指数分布族的自然参数

即y的条件分布的自然参数能被x线性表达，如若设$E[y|x]=\mu$，那么根据$g(E[y|x])={\beta }^{\prime }x$，能推得$\theta =g(\mu )$。我们称满足这样条件的连接函数g为正则连接函数。通常我们的GLM模型都带上这一点假设，因此我们常用的都是正则连接函数。

如何找这样的g？

利用指数分布族，能够有效的找到g.
根据指数分布族的性质：

• $\mu =E(y|x)=b^{\prime }(\theta )$

=> $g(b^{\prime }(\theta ))=\theta$
=> $g(\mu )=(b^{\prime }{)}^{-1}(\mu )$

也即正则连接函数g为b的一阶倒数的反函数。因此，对于整个GLM模型，最重要的是确定y的条件分布，并将其写成指数分布族的形式，确定自然参数，由此可得模型的正则连接函数。

模型详解

在了解完GLM的两个基础与假设后，我们来看GLM的模型拟合。这一部分其实也即是参数估计，我们在得到样本数据后，根据样本因变量的分布，确定需要拟合什么样的GLM模型，进而估计GLM模型的回归系数(GLM的参数就是$\theta ={\beta }^{\prime }x$中的$\beta$，也即回归系数)

参数估计

极大似然估计

通常谈到参数估计，在假定服从相关分布后，我们首先想到的便是MLE极大似然估计。这里我们将不讨论其余机器学习类方法如交叉墒，自定损失函数等方法。 极大似然估计的方法这里不再详述，仅叙述在GLM中如何使用。根据我们的假设与指数分布族形式：

• $\theta ={\beta }^{\prime }x$
• $l(\beta )={\sum }_{i=1}^n(\frac{y_i{\theta }_i-b({\theta }_i)}{a(\varphi )}-c(y_i,\varphi ))$

=>$l(\beta )={\sum }_{i=1}^n(\frac{y_i(x_i^{\prime }\beta )-b(x_i^{\prime }\beta )}{a(\varphi )}-c1)$
其中c1与$\beta$无关，在后续求导时能消去，由此可推的对数似然函数。后面再对${\beta }_i$求梯度并令其为0，可依次得到参数的解析解。
当然上面是理想情况，并不是所有似然函数都能有解析解，在相当大的情况下，函数没有解析解，因此只能依赖梯度下降或梯度上升，牛顿-拉弗森等优化方法进行求解，参数可能不是全局最优，那这就是优化的问题了，具体可参考Adam等深度学习优化器…当然GLM的似然函数都是凸的，意味着普通的优化方法都能得到全局最优解。（只要迭代次数够多）

Newton-Raphson Method

牛顿迭代法，也即牛顿-拉弗森法，是一种常用的用于求极值的方法，其核心是泰勒展开二阶近似，通用公式为：
${\beta }^{(t+1)}={\beta }^{(t)}-\frac{f({\beta }^{(t)})}{f^{\prime }({\beta }^{(t)})}$
其中$\beta$为参数，f为损失函数。如果这里将f换为我们上面定义的对数似然函数的导数$l^{\prime }(\beta )$，那么迭代公式变为：
${\beta }^{(t+1)}={\beta }^{(t)}-\frac{l^{\prime }({\beta }^{(t)})}{l^{\prime \prime }({\beta }^{(t)})}$
若写成矩阵形式，做如下标记：
$u^{(t)}=\nabla l({\beta }^{(t)})$
$H^{(t)}={\nabla }^{2}l({\beta }^{(t)})$
则迭代公式为：
${\beta }^{(t+1)}={\beta }^{(t)}-(H^{(t)}{)}^{-1}{u}^{(t)}$

Fisher Scoring Method

Fisher法是牛顿法的一种替代，仅将牛顿迭代公式中的Hessian矩阵(即H)换为Fisher information矩阵即可。
记$J^{(t)}=-E[{\nabla }^{2}l({\beta }^{(t)})]$
则Fisher法的迭代公式为：
${\beta }^{(t+1)}={\beta }^{(t)}-(J^{(t)}{)}^{-1}{u}^{(t)}$

Iteratively Reweighted Least Squares

这种方法有点像局部线性回归，具体如下：

关于FS和IRLS

可能有人会对后两种方法有疑问，FS和IRLS中的J和W怎么计算？这个时候指数分布族和正则连接函数的作用就体现出来了。以下都只给出结论：

• $J=X^{\prime }WX$
• W为对角矩阵，$W_{ii}=\frac{1}{(g^{\prime }({\mu }_i){)}^{2}Var(y_i)}$
• $Var(y_i)=b^{\prime \prime }(\theta )a(\varphi )$

因此，利用g和b，可以很轻松求得J和W。如以下例子：

区间估计

其实在GLM中，J和W的作用非常大，不只是上面的优化。经过证明发现，回归系数$\hat{\beta }-{\beta }^{\ast }$近似服从$N(0,{\hat{J}}^{(-1)})$。利用这点性质，可为参数建立区间估计，因此不难写出，${\beta }_i$的$1-\alpha$置信区间为：
$(\widehat{{\beta }_i}-\sqrt{({\hat{J}}^{-1}{)}_{ii}}{\Phi }^{-1}(1-\alpha /2),\widehat{{\beta }_i}+\sqrt{({\hat{J}}^{-1}{)}_{ii}}{\Phi }^{-1}(1-\alpha /2))$

除了利用MLE的渐近性，还可以利用W进行区间估计。以预测区间为例，不加证明给出以下结论：
若记$\eta =X^{\prime }\beta$，根据$Cov(\hat{\beta })={\hat{J}}^{-1}=(X^{\prime }WX{)}^{-1}$，有：
$Cov(\hat{\eta })=XCov(\hat{\beta })X^{\prime }\approx X(X^{\prime }WX{)}^{-1}{X}^{\prime }$

其实到了这部分，和传统的线性回归模型也没什么差异了，最终还是回到了回归系数的性质研究上。利用回归系数的渐近性，可以用类似的研究方法拓展到GLM回归系数的研究，包括参数区间估计，假设检验。

模型检验

GLM模型的检验，与普通线性回归的检验差不多，方法都是观察残差与预测值的图来判断模型效果。但GLM的残差并不是简单的残差，而有不同的计算方式。下面介绍几种残差，如果拟合不错，残差与预测值的图将在0附近均匀分布，这一点与线性回归的检验相差不大。

Pearson Residuals

Pearson Residuals定义如下：

$\widehat{e_i}=\frac{y_i-\widehat{{\mu }_i}}{\sqrt{Var(\widehat{{\mu }_i}})}$

$\widehat{e_i}$近似服从标准正态分布，在与$\widehat{y_i}$的散点图中将均匀分布在0附近。

Deviance Residuals

首先定一个相关统计量：

• $d_i=2w_i[y_i(\widetilde{{\theta }_i}-\widehat{{\theta }_i})-b(\widetilde{{\theta }_i})+b(\widehat{{\theta }_i})]$
• $\widetilde{{\theta }_i}=g(y_i)$
• $\widehat{{\theta }_i}=g(y_i)$

Deviance Residuals定义如下：
$\widehat{{ϵ}_i}=\sqrt{d_i}\times sign(y_i-\widehat{{\mu }_i})$

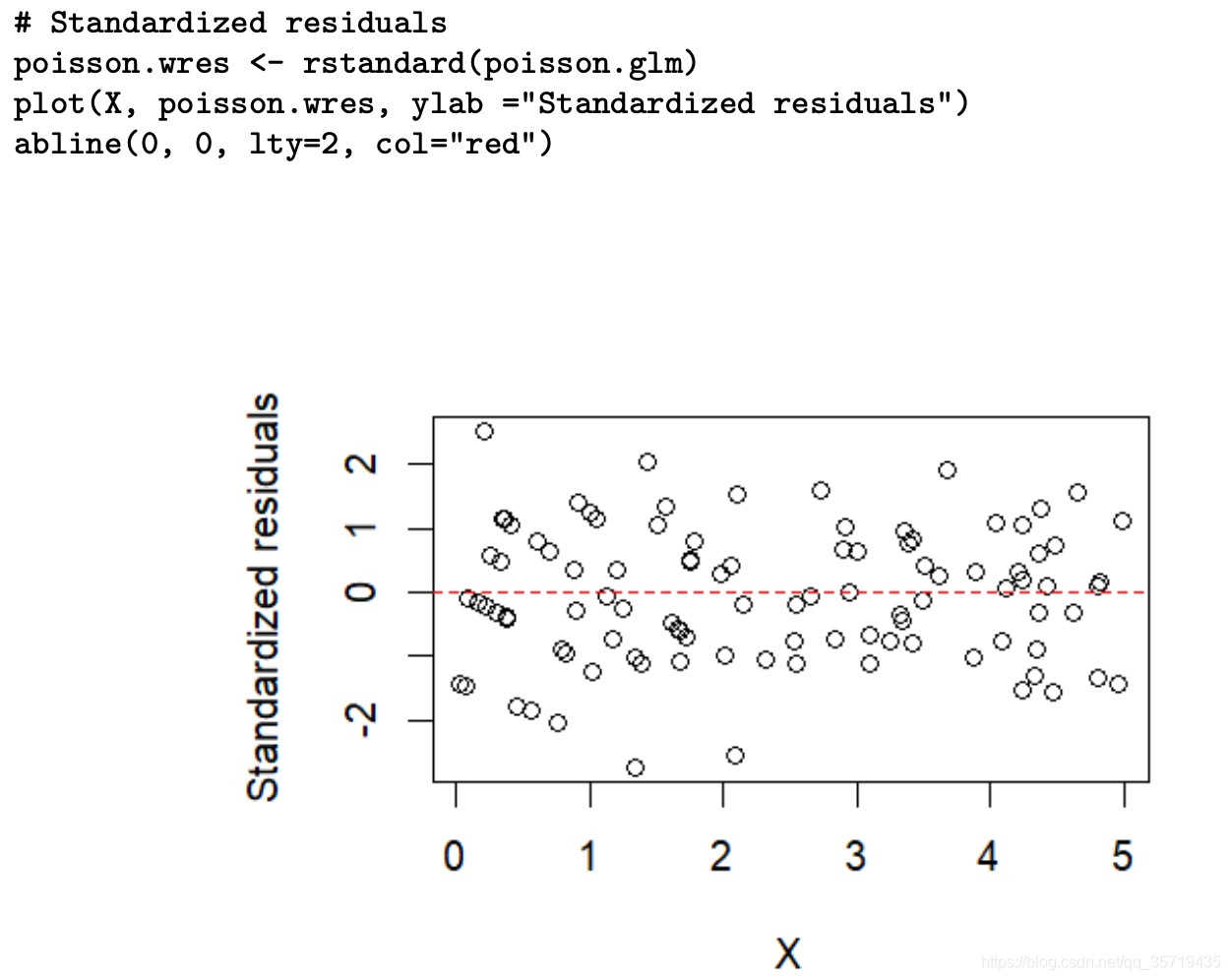
Standardized residuals

Pearson residuals 和 Deviance residuals倾向于低估残差的方差。和线性回归的标准化残差计算方法一样，GLM中Standardized residuals计算只是修改了方差的估计，计算方法如下：

• $\widehat{{ϵ}_i}=y_i-\widehat{{\mu }_i}$
• $Var(\widehat{{ϵ}_i})\approx Var({\mu }_i)(1-h_i)$
• $\widehat{e_i}=\frac{\widehat{{ϵ}_i}}{\sqrt{Var(\widehat{{ϵ}_i})}}$