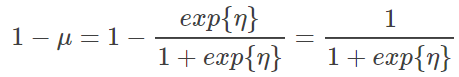1.广义线性模型和glm()函数
广义线性模型扩展了线性模型的框架,它包含了非正态因变量的分析。
广义线性模型通过拟合响应变量的条件均值的一个函数(不是响应变量的条件均值),假设响应变量服从指数分布族中的某个分布(并不仅限于正态分布),极大地扩展了标准线性模型。模型参数估计的推导依据的是极大似然估计,而非最小二乘法。
(1)与glm()连用的函数
| 函数 | 描述 |
| summary | 展示拟合模型的细节 |
| Coefficients()、coef() | 列出拟合模型的参数(截距项和斜率) |
| Confint() | 给出模型参数的置信(默认为95%) |
| Residuals() | 列出拟合模型的残差值 |
| Anova() | 生成两个拟合模型的方差分析表 |
| Plot() | 生成评价拟合模型的诊断图 |
| Predict() | 用拟合模型对新数据集进行预测 |
(2)模型拟合和回归诊断
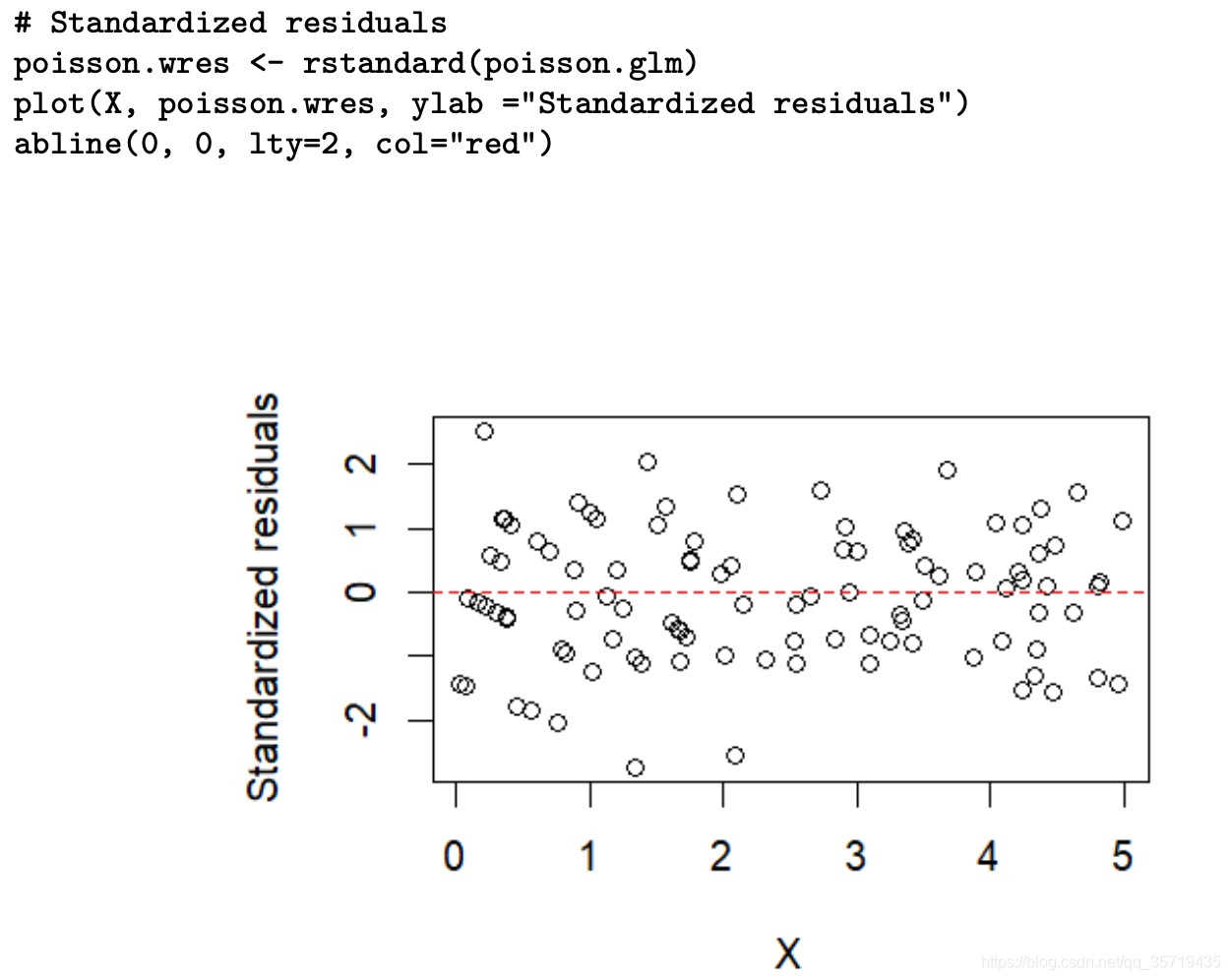
当评价模型的适用性时,可以绘制初始响应变量的预测值与残差的图形
Eg:
Plot(predict(model,type=”response”),residuals(model,type=”deviance”))R中列出帽子(hat value)、学生化残差值和Cook距离统计量的近似值
对于识别异常点的阈值,并没有统一答案,都是通过相互比较来进行判断的
可绘制各统计量的参考图,然后找出异常大的值
Eg
Plot(hatvalues(models))
Plot(rstudent(model))
Plot(cooks.distance(model))
还可以:
Library(car)
InfluencePlot(model)
2. Logistic回归
(1)Logistic
当通过一系列连续型和/或类别型预测变量来预测二值型结果变量时,Logistic回归是一个非常有用的工具。
Eg:
AER包中的数据框Affairs为例
install.packages("AER")
library(AER)
data(Affairs,package="AER")
summary(Affairs)
Affairs$ynaffair[Affairs$affairs>0]<-1
Affairs$ynaffair[Affairs$affairs==0]<-0
Affairs$ynaffair<-factor(Affairs$ynaffair,levels=c(0,1),labels=c("No","Yes"))
table(Affairs$ynaffair)
fit.full<-glm(ynaffair~gender+age+yearsmarried+children+religiousness+education+occupation+rating,data=Affairs,family=binomial())
summary(fit.full)

fit.reduced<-glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family=binomial())
summary(fit.reduced)

新模型的每个回归系数都非常显著,由于两模型嵌套,故可以使用anova()函数对它们进行比较,对于广义线性回归,可用卡方检验。
anova(fit.reduced,fit.full,test="Chisq")
(2)解释模型参数
先看回归系数
coef(fit.reduced)
因对数优势化解释性差,故可对结果进行指数化
exp(coef(fit.reduced))
若有需要还可使用confit()函数获取系数的置信区间
(3)评价预测变量对结果概率的影响
使用predict()观察某个预测变量在各个水平时对结果概率的影响
testdata<-data.frame(rating=c(1,2,3,4,5),age=mean(Affairs$age),yearsmarried=mean(Affairs$yearsmarried),religiousness=mean(Affairs$religiousness))
testdata
testdata$prob<-predict(fit.reduced,newdata=testdata,type="response")
testdata
testdata<-data.frame(rating=mean(Affairs$rating),age=seq(17,57,10),yearsmarried=mean(Affairs$yearsmarried),religiousness=mean(Affairs$religiousness))
testdata
testdata$prob<-predict(fit.reduced,newdata=testdata,type="response")
testdata
(4)过度离势
过度离势会导致奇异的标准误检验和不精确的显著性检验
当出现过度离势时,仍可使用glm()函数拟合Logistic回归,但此时需要将二项分布必为类二项分布(quasibinomial distribution)
检测过度离势的一种方法是比较二项分布模型的残差偏差与自由度,若比值:r=残差偏差/残差自由度 ,比1大很多,便认为是存在过度离势。
还可对过度离势进行检验:需拟合模型两次,第一次使用family="binomial",第二次使用family="quasibinomial"
fit<-glm(ynaffair~age+yearsmarried+religiousness+rating,family=binomial(),data=Affairs)
fit.od<-glm(ynaffair~age+yearsmarried+religiousness+rating,family=quasibinomial(),data=Affairs)
pchisq(summary(fit.od)$dispersion*fit$df.residual,fit$df.residual,fit$df.residual,lower=F)(5)扩展
3.泊松回归
当通过一系列连续型和/或类别型预测变量来预测计数型结果变量时,泊松回归是一个非常有用的工具。
利用robust 包中的Breslow癫痫数据
install.packages("robust")
library(robust)
data(breslow.dat,package="robust")
names(breslow.dat)
summary(breslow.dat[c(6:8,10)])
opar<-par(no.readonly=TRUE)
par(mfrow=c(1,2))
attach(breslow.dat)
hist(sumY,breaks=20,xlab="Seizure Count",main="Distribution of Seizures")
boxplot(sumY~Trt,xlab="Treatment",main="Group Comparisons")
par(opar)
fit<-glm(sumY~Base+Age+Trt,data=breslow.dat,family=poisson())
summary(fit)
(1)解释模型参数
使用coef()函数可获取模型系数,或调用summary()函数的输出结果中的Coefficients表格
coef(fit)
exp(coef(fit))

与Logistic回归中的指数化参数相似,泊松模型中的指数化参数对响应变量的影响都是成倍增加的,而不是线性相加。
(2)过度离势
泊松分布的方差和均值相等,当响应变量观测的方差比根据汽枪颁预测的方差在时,泊松回归可能发生过度离势。
可能发生过度离势的原因有如下几个:
遗漏了某个重要的预测变量;
可能因为事件相关;
在纵向数据分析中,重复测量的数据由于内在群聚特性可导致过度离势。此处暂不讨论纵向泊松模型。
与Logisitic回归类似,此处如果残差偏差与残差自由度的给远远大于1,则表明存在过度离势。
qcc包提供了一个对泊松模型过度离势的检验方法
install.packages("qcc")
library(qcc)
qcc.overdispersion.test(breslow.dat$sumY,type="poisson")
p<0.05,进一步表明确实存在过度离势。
通过用family="quasipoisson"替换family="poisson",仍可使用glm()函数对该数据进行拟合,与Logistic回归中处理过度离势的方法是相同的。
fit.od<-glm(sumY~Base+Age+Trt,data=breslow.dat,family=quasipoisson())
summary(fit.od)
(3)扩展
时间段变化的泊松回归
fit<-glm(sumY~Base+Age+Trt,data=breslow.dat,offset=log(time),family=poisson())零膨胀的泊松回归
稳健泊松回归